线段树合并笔记
线段树合并笔记
定义:
定义其实就是字面意思,就是将两棵线段树合并在一起,至于我们为什么要合并,我们可以先可以看道例题。
Lomsat gelral
题面翻译
- 有一棵 \(n\) 个结点的以 \(1\) 号结点为根的有根树。
- 每个结点都有一个颜色,颜色是以编号表示的, \(i\) 号结点的颜色编号为 \(c_i\)。
- 如果一种颜色在以 \(x\) 为根的子树内出现次数最多,称其在以 \(x\) 为根的子树中占主导地位。显然,同一子树中可能有多种颜色占主导地位。
- 你的任务是对于每一个 \(i\in[1,n]\),求出以 \(i\) 为根的子树中,占主导地位的颜色的编号和。
- \(n\le 10^5,c_i\le n\)
分析:
我们先考虑这道题的暴力的做法,就是对于每个节点直接 dfs 暴力求一下这棵子树中的每个颜色的数量,然后取最大值,那么显然易见肯定会超时。
我们先想一想为什么会超时
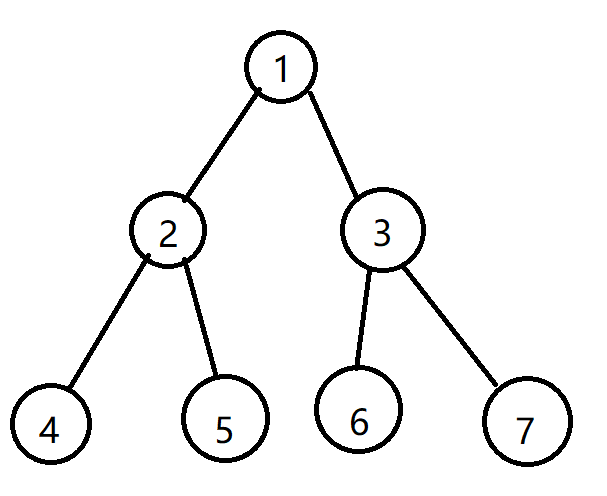
对于这么一张图,当我们扫描 3 号节点的子树时候会将 3, 6, 7都扫描到,而当我们再统计 1 号节点的答案时会再将 3 号节点的子树搜一遍,这样就会有大量的重复计算,实际上 1 号节点是可以通过 2 号节点和 3 号节点答案去拼凑出来的,那么这个拼凑的过程其实就是将以 2 号节点为根的线段树和以 3 号节点为根的线段树进行合并。
那么我们如何合并呢?在学之前你需要知道权值线段树和动态开点。
什么??你不会 那我就稍微讲一讲,我们一开始学的线段树,对于每个节点的 l 和 r 实际上维护的是一个数组或是别的数据结构的下标,但但是我们会发现这样如果让统计一个区间的某个值出现的次数就很难维护,那么这时候就可以使用我们的权值线段树了,与普通线段树不同的是我们此时每个节点的 l 和 r 维护并不再是下标而是一个值域,比如一个节点的 l 是 3, r 是 8,那么我们这个节点所维护的就是数值大小在 3 和 8 之间的数出现的次数。这就是权值线段树的基本思想。
但是如果仅仅是这样还是不够,因为你会发现,当题干中的值域范围非常大的时候,我们的权值线段树是开不下的,那么我们还要维护,那么我们考虑对原有的权值线段树进行压榨,我们其实可以想到,对于一颗权值线段树,我们的每个节点是不一定有数字,而这样的节点对于答案是没有任何贡献的,而且往往这样的节点会很多,因此我们可以在建线段树的时候先不把这些空的节点都建出来,而是用到了一个节点再建一个节点。
比如对于这么一棵树(每个节点下面的数字就是 l 和 r,也就是值域)
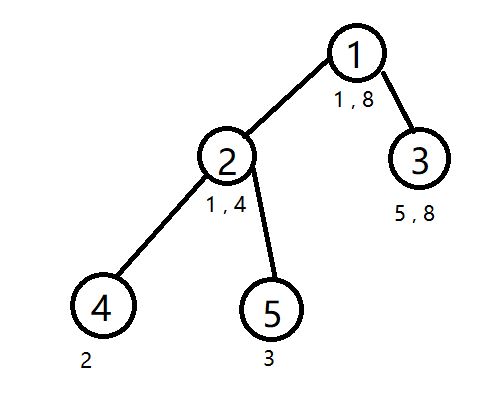
我们会发现 2 号节点虽然有着 l 和 r ,但是他只连了值域为 2 的 4 号节点和值域 为 3 的 5 号节点,为什么没有连值域为 1 和 4 的节点呢,因为如果我们没有这些数,实际上就没有创建他们的必要了(因为对答案肯定是没有贡献的),那么如果你再插入一个值域为 6 的节点怎么办呢?那你就直接给 3 号节点加个新的儿子并将他的值域设成 6 即可。
那么你会发现如果我分别加了1,2,3,4值域的节点,我刚才的那个图的 2 号节点会有 4 个儿子了,这就有点不太符合线段树的结构了,那么我们此时可以再让 l 和 r 的意义又变成了下标。那么你肯定又会有疑问了,那我怎么确定值域呢??
我们可以先看着代码理解一下
void insert(int &u, int l, int r, int val)
{
if(!u) //如果没有这个节点就新建一个
u = ++ cnt; //cnt为节点的编号
if(l == r) //入如果已经到了叶子节点,就证明找到了这个点,直接将总和加一即可
{
tr[u].sum ++;
return ;
}
int mid = l + r >> 1; //二分值域
if(val <= mid) //如果当前值小于中点,证明应该插在当前节点的左子树
insert(tr[u].l, l, mid, val); //递归建树
else //反之
insert(tr[u].r, mid + 1, r, val);
pushup(u); //更新父亲
}
这是新建一个节点的代码,这里面的 l 和 r 是值域, val 是你要插入的值域的点。
那么看到这里你应该大致的明白了动态开点和权值线段树了,权值线段树常常和动态开点相结合,上面的那个代码就是一个动态开点的权值线段树。同时如果动态开点,值域还是过大怎么办,那么我们就可以对每个数进行离散化,因为往往用到权值线段树的时候统计的基本上都是数量,所以数值和数值之间只用体现大小关系即可。
然后我们回来接着看这道题

对于这棵树如果我们已经有了 3 号节点和 2 号节点的答案,我们怎么更新 1 号节点呢?
那么你刚才学完了权值线段树,你肯定会有一个想法,就是将 2 号节点和 3 号节点的权值线段树合并一下就行了。
那么怎么合并呢???
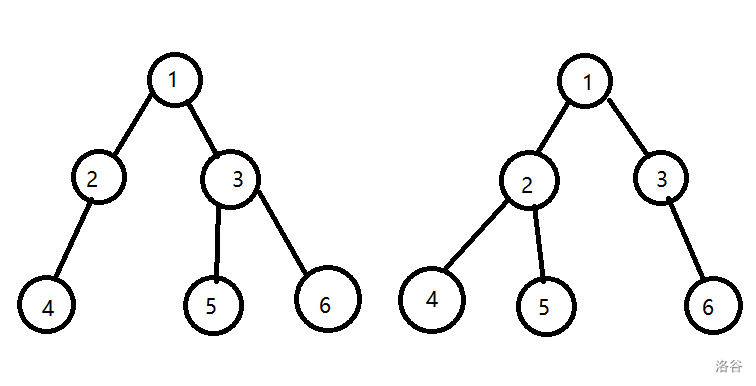
比如现在我们要合并这两棵子树,我们合并线段树,肯定是合并对应位置的节点,保证结构不变比如当我们合并左边这棵树的 2 号节点和右边 2 号节点子树,这时两棵树的这个位置都有节点,那么我们就可以直接将右边子树的值加到左边子树,但是当我们合并左边那棵树的时候,5号节点的对应到右边的位置是没有点的,那么我们这时候直接将存在的这个点继承过去即可,合并好之后的就是这样一棵树。
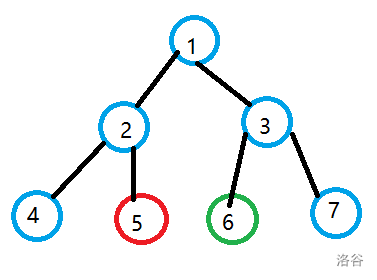
其中蓝色的点是将左右子树都存在的点合并得到的,红色的点是左边有,右边没有,直接将左边的点继承过来得到的,绿色就是右边有左边没有。
那么相信你看到这里你应该就理解了如何合并线段树了,那么刚才那道例题你应该就能写出来了。
我会在代码里对细节进行一些说明
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
namespace read_write //无关紧要的快读快写
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
}
namespace Segment_Tree
{
using namespace read_write;
const int N = 2e6 + 10;
int n, m;
int h[N], idx;
int col[N], ans[N];
int rt[N], cnt;
struct Tree
{
int l, r;
int val, sum, ans;
} tr[N];
struct Edge
{
int ne, v;
} e[N];
void pushup(int u) //ans是题干当中的颜色编号之和,val是颜色最多的编号,sum是数量
{
if(tr[tr[u].l].sum > tr[tr[u].r].sum)
{
tr[u].sum = tr[tr[u].l].sum;
tr[u].val = tr[tr[u].l].val;
tr[u].ans = tr[tr[u].l].ans;
}
if(tr[tr[u].l].sum == tr[tr[u].r].sum)
{
tr[u].sum = tr[tr[u].l].sum;
tr[u].val = tr[tr[u].l].val;
tr[u].ans = tr[tr[u].l].ans + tr[tr[u].r].ans;
}
if(tr[tr[u].l].sum < tr[tr[u].r].sum)
{
tr[u].sum = tr[tr[u].r].sum;
tr[u].val = tr[tr[u].r].val;
tr[u].ans = tr[tr[u].r].ans;
}
}
void insert(int &u, int l, int r, int pos, int v) //新建一个节点,刚才已经说过了,就不再说了
{
if(!u)
u = ++ cnt;
if(l == r)
{
tr[u].sum += v;;
tr[u].val = l;
tr[u].ans = l;
return ;
}
int mid = l + r >> 1;
if(pos <= mid)
insert(tr[u].l, l, mid, pos, v);
else
insert(tr[u].r, mid + 1, r, pos, v);
pushup(u);
}
int merge(int a, int b, int l, int r) //合并线段树
{
if(!a) //如果有一个位置为空,返回不空的位置即可
return b;
if(!b)
return a;
if(l == r) //如果到了那个节点,就将两棵树的答案合并即可
{
tr[a].sum += tr[b].sum;
tr[a].val = l;
tr[b].ans = l;
return a;
}
int mid = l + r >> 1;
tr[a].l = merge(tr[a].l, tr[b].l, l, mid);
tr[a].r = merge(tr[a].r, tr[b].r, mid + 1, r);
pushup(a);
return a;
}
void dfs(int u, int fath) //递归子树,获得答案
{
for(int i = h[u] ; i ; i = e[i].ne)
{
int v = e[i].v;
if(v == fath)
continue;
dfs(v, u); //先搜子树,保证子树的答案比父亲先算出来
merge(rt[u], rt[v], 1, 100000); //将当前节点和他的叶子节点合并
}
insert(rt[u], 1, 100000, col[u], 1); //等得到这个节点的答案之后再将这个节点插入,因为我们要统计的是子树中的答案,是不包含当前节点的
ans[u] = tr[rt[u]].ans;
}
}
namespace Solve
{
using namespace Segment_Tree;
void add(int u, int v)
{
e[++ idx].v = v, e[idx].ne = h[u], h[u] = idx;
}
void solve()
{
read(n);
for(int i = 1 ; i <= n ; ++ i)
{
read(col[i]);
rt[i] = i;
++ cnt; //先将根节点创建出来
}
for(int i = 1 ; i < n ; ++ i)
{
int u, v;
read(u), read(v);
add(u, v);
add(v, u);
}
dfs(1, 0);
for(int i = 1 ; i <= n ; ++ i)
write(ans[i]), putchar(' ');
}
}
signed main()
{
Solve::solve();
return 0;
}
怎么样,是不是觉得自己对线段树合并已经有一个初步的认识了
那么我再放几道例题练练手??
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
为啥我不照着模板题讲呢,因为我觉得其实刚才那道题更好理解。你仔细读完题之后会发现其实这道题跟刚才那道题一摸一样,也是对于每个节点建一棵权值线段树,当然这里是对许多树进行操作,你可以通过差分维护。
(你可能会发现我这道题的码风和刚才的不太一样,因为这道题是老早之前写的了)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e6 + 10;
const int maxn = 1e5;
int n, m, tot;
int root[N], ans[N];
int L[N], R[N], mx[N], id[N]; //mx:数量的最大值 id:最大数量的袋子id
int dep[N], fa[N][22];
int h[N], e[N], ne[N], idx;
inline void write(int a)
{
if(a < 0)
{
a = -a;
putchar('-');
}
if(a > 9)
write(a / 10);
putchar(a % 10 + '0');
}
inline void read(int &a)
{
int x = 0,f = 1;
char ch = getchar();
while(ch < '0' || ch > '9')
{
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9')
x = x * 10 + ch - '0',ch = getchar();
a = x * f;
}
inline void add(int a,int b)
{
e[++ idx] = b,ne[idx] = h[a],h[a] = idx;
}
inline void dfs1(int a,int f) //预处理一下深度和祖先
{
dep[a] = dep[f] + 1;
fa[a][0] = f;
for(register int i = 1 ; i <= 20 ; i ++ )
{
fa[a][i] = fa[fa[a][i - 1]][i - 1];
}
for(register int i = h[a] ; ~i ; i = ne[i] )
{
int j = e[i];
if(j == f)
continue;
dfs1(j,a);
}
}
inline int lca(int a,int b) //求最近公共祖先
{
if(dep[a] < dep[b])
swap(a,b);
for(register int i = 20 ; i >= 0 ; i -- )
{
if(dep[fa[a][i]] >= dep[b])
a = fa[a][i];
}
if(a == b)
return a;
for(register int i = 20 ; i >= 0 ; i -- )
{
if(fa[a][i] != fa[b][i])
{
a = fa[a][i];
b = fa[b][i];
}
}
return fa[a][0];
}
inline void pushup(int p) //更新父节点的值
{
if(mx[L[p]] >= mx[R[p]]) //如果左大于右,将当前点更新
{
mx[p] = mx[L[p]]; //将最大值更换同时换id
id[p] = id[L[p]];
}
else
{
mx[p] = mx[R[p]];
id[p] = id[R[p]];
}
}
inline int modify(int p,int l,int r,int x,int val) //创建新的节点
{
if(!p)
p = ++ tot;
if(l == r)
{
mx[p] += val;
id[p] = x;
return p;
}
int mid = (l + r) >> 1;
if(x <= mid)
L[p] = modify(L[p], l, mid, x, val);
else
R[p] = modify(R[p], mid + 1, r, x, val);
pushup(p);
return p;
}
inline int merge(int a,int b,int l,int r) //合并
{
if(!a)
return b;
if(!b)
return a;
if(l == r)
{
mx[a] += mx[b]; //将b的信息遗传到a,然后返回a
return a;
}
int mid = (l + r) >> 1;
L[a] = merge(L[a], L[b], l, mid);
R[a] = merge(R[a], R[b], mid + 1, r);
pushup(a);
return a;
}
inline void dfs(int u,int f) //宽搜找答案
{
for(register int i = h[u] ; ~i ; i = ne[i])
{
int j = e[i];
if(j == f)
continue;
dfs(j,u);
root[u] = merge(root[u], root[j], 1, maxn);
}
if(mx[root[u]])
ans[u] = id[root[u]];
}
int main()
{
memset(h, -1,sizeof h);
read(n),read(m);
for(register int i = 1 ; i < n ; i ++ )
{
int a,b;
read(a),read(b);
add(a,b);
add(b,a);
}
dfs1(1,0);
for(register int i = 1 ; i <= m ; i ++ )
{
int x,y,z;
read(x),read(y),read(z);
int f = lca(x,y);
int p = fa[f][0];
root[x] = modify(root[x], 1, maxn, z, 1);
root[y] = modify(root[y], 1, maxn, z, 1);
root[f] = modify(root[f], 1, maxn, z, -1);
if(p)
root[p] = modify(root[p], 1, maxn, z, -1);
}
dfs(1,0);
for(register int i = 1 ; i <= n ; i ++ )
{
write(ans[i]);
puts("");
}
return 0;
}
Promotion Counting P
这道题也比较的板子,就维护一下最大值即可,其实也可以不维护,直接建完,然后查询一下合并之后的线段树中的大于这头牛的值的个数也是可以的。
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
}
namespace Segment_Tree
{
using namespace read_write;
const int N = 2e6 + 10;
int n, m;
int h[N], idx;
int ans[N], cnt, tot;
int rt[N], w[N], a[N];
struct Edge
{
int ne, v;
} e[N];
void add(int u, int v)
{
e[++ idx].v = v, e[idx].ne = h[u], h[u] = idx;
}
struct Tree
{
int l, r;
int sum;
} tr[N];
void pushup(int u)
{
tr[u].sum = tr[tr[u].l].sum + tr[tr[u].r].sum;
}
void insert(int &u, int l, int r, int pos)
{
if(!u)
u = ++ tot;
if(l == r)
{
tr[u].sum ++ ;
return ;
}
int mid = l + r >> 1;
if(pos <= mid)
insert(tr[u].l, l, mid, pos);
else
insert(tr[u].r, mid + 1, r, pos);
pushup(u);
}
int merge(int a, int b, int l, int r)
{
if(!a)
return b;
if(!b)
return a;
if(l == r)
{
tr[a].sum += tr[b].sum;
return a;
}
int mid = l + r >> 1;
tr[a].l = merge(tr[a].l, tr[b].l, l, mid);
tr[a].r = merge(tr[a].r, tr[b].r, mid + 1, r);
pushup(a);
return a;
}
int query(int u, int l, int r, int L, int R)
{
if(L <= l && R >= r)
return tr[u].sum;
int mid = l + r >> 1;
int res = 0;
if(L <= mid)
res += query(tr[u].l , l, mid, L, R);
if(R > mid)
res += query(tr[u].r , mid + 1, r, L, R);
return res;
}
void dfs(int u, int fath)
{
for(int i = h[u] ; i ; i = e[i].ne)
{
int v = e[i].v;
if(v == fath)
continue;
dfs(v, u);
merge(rt[u], rt[v], 1, cnt);
}
ans[u] = query(rt[u], 1, cnt, w[u] + 1, cnt);
//write(ans[u]), puts("");
}
}
namespace Solve
{
using namespace Segment_Tree;
void solve()
{
read(n);
for(int i = 1 ; i <= n ; ++ i)
{
read(w[i]);
a[i] = w[i];
}
std::sort(a + 1, a + n + 1);
cnt = std::unique(a + 1, a + n + 1) - a - 1;
for(int i = 1 ; i <= n ; ++ i)
{
w[i] = std::lower_bound(a + 1, a + n + 1, w[i]) - a;
insert(rt[i], 1, cnt, w[i]);
}
for(int i = 2; i <= n ; ++ i)
{
int x;
read(x);
add(x, i);
add(i, x);
}
dfs(1, 0);
for(int i = 1 ; i <= cnt ; ++ i)
write(ans[i]), puts("");
}
}
int main()
{
Solve::solve();
return 0;
}
到了最后再给大家推荐一个线段树合并的题单,可以自己再练练手。
题单
完结撒花★,°:.☆( ̄▽ ̄)/$:.°★ 。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号