开源库Eigen

一、Eigen 基本功能测试

1. 基本调用编译流程

1.1.1 程序编写

#include <iostream>
#include <Eigen/Dense>

using Eigen::MatrixXd;

int main()
{
  MatrixXd m(2,2);
  m(0,0) = 3;
  m(1,0) = 2.5;
  m(0,1) = -1;
  m(1,1) = m(1,0) + m(0,1);
  std::cout << m << std::endl;
}

1.1.2 编译执行

g++ -I /home/pi/WorkSpace/eigen eigen_demo.c -o eigen_demo

执行结果如下：

1.1.3 Eigen项目编译

1. 下载Eigen官网的程序安装包
2. 解压安装包并进入安装包：cd ./eigen && mkdir cmake_test && cd cmake_test
3. 执行 cmake 命令：cmake ../
4. 开始编译并安装：make && make install
   

2. Eigen各模块调用测试

Eigen基础使用库函数 官方文档翻译 Markdown

• Core：Matrix和Array类，基础的线性代数运算和数组操作；
• Geometry：旋转，平移，缩放，2维和3维的各种变换；
• LU：求逆，行列式，LU分解；
• Cholesky：LLT和LDLT Cholesky分解；
• Householder：Householder变换；
• SVD：SVD分解；
• QR：QR分解。
• Eigenvalues：特征值，特征向量分解。
• Sparse：稀疏矩阵的存储和运算。
• Dense：包含了Core、Geometry、LU、Cholesky、SVD、QR、Eigenvalues等模块。
• Eigen：包含了Dense和Sparse模块。

1.2.1 矩阵基本运算

Eigen::MatrixXf matrix1(2, 3);
Eigen::MatrixXf matrix2(2, 3);
Eigen::Vector3f vec1;
matrix1 << 1, 2, 3, 4, 5, 6;
matrix2 << 7, 8, 9, 10, 11, 12;
vec1 << 1.1 , 2.1, 4.2;

1. 矩阵加减乘除，尺度缩放

   matrix1 + matrix2
   matrix1 - matrix2 // 维度相同的矩阵何向量可以加减
   matrix1 * 2 // Scale 尺度因子缩放
   matrix1 / 2 // Scale 尺度因子缩放
   
   Eigen::MatrixXf matrix3(3,2);
   matrix3 * matrix2 // 前一个矩阵列数需要与下一个矩阵的行数相同才能计算
   
   Eigen::Vector3d v(1, 2, 3);
   Eigen::Vector3d w(0, 1, 2);
   cout << "Cross product:\n" << v.cross(w) << endl; // 向量叉乘
   cout << "Cross product:\n" << v.dot(w) << endl;  // 向量点乘
   
   Eigen::VectorXd w(4);
   Eigen::MatrixXd M(4,4);
   M = MatrixXd::Random(4,4);
   cout << M * w << endl;
   

2. 矩阵转置、共轭、共轭转置

   matrix1.transpose() // 直接调用类接口进行矩阵的转置
   matrix1.conjugate() // 矩阵共轭
   matrix1.adjoint() // 矩阵共轭 + 转置
   

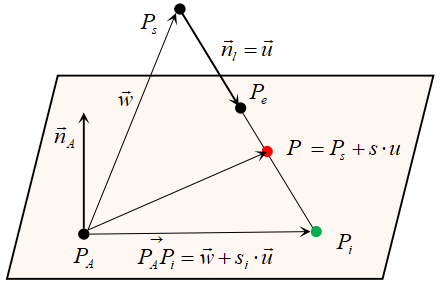
3. 空间直线与平面的交点
   

   1. 直线的定义：
      1. 确定空间直线上的两个点，一个作为起始点 \(P_s\) ，一个作为终止点 \(P_e\)
      2. 通过起始点和终止点计算直线的方向向量： \(\vec{n_l} = P_e - P_s\)
      3. 直线方程的向量表示为：\(l:P = P_s + s\cdot \vec{n_l}\)
   2. 平面的定义：
      1. 确定平面上的一个点 \(P_A\)，确定一个平面的法向量 \(\vec{n_A}\)
      2. 平面的方程表示为： \(\vec{n_A}\cdot(P-P_A) = 0\)
   3. 平面与直线的交点定义：
      1. 直线与平面平行时 (\(\vec{n_l} \perp \vec{n_A}\))，当直线上的某一点在平面上，则直线在平面内；反之处于平行状态
      2. 直线与平面相交时：
      \[\vec{n_A} \cdot \vec{P_AP_i} = 0 \rArr \vec{n_A} \vec{w} + s_i \vec{n_A} \vec{u} = 0 \rArr s_i = -\frac{\vec{n_A} \vec{w}}{\vec{n_A} \vec{u}} = \frac{\vec{n_A}\cdot (P_A - P_s)}{\vec{n_A} \cdot (P_e - P_s)} \]

代码实现： 🌻

Eigen::Vector3d LinePlaneIntersection(const Eigen::Vector3d &u, const Eigen::Vector3d &ps, const Eigen::Vector3d &nA, const Eigen::Vector3d &pA)
{
	double s = (nA.dot(pA) - nA.dot(ps))/nA.dot(u);
	return s * u + ps;
}

测试结果：

1.2.2 矩阵高级用法

二、Eigen C/C++ 数据结构转化

typedef struct{
    double x;
    double y;
    double z;
}T_A391_AXIS_DATA;

Eigen::Vector3f vector_pos;
T_A391_AXIS_DATA t_pos;
// C++ vector模板数据转C语言结构体
t_pos.x = vector_pos[0]
t_pos.y = vector_pos[1]
t_pos.z = vector_pos[2]
// C语言结构体数据转C++ vector模板
vector_pos[0] = t_pos.x
vector_pos[1] = t_pos.y
vector_pos[2] = t_pos.z

Reference

1. Documents
2. 中文文档
3. HomePage
4. 其他