Part1 - 轮式小车运动学分析

一、滑移式车体运动学模型

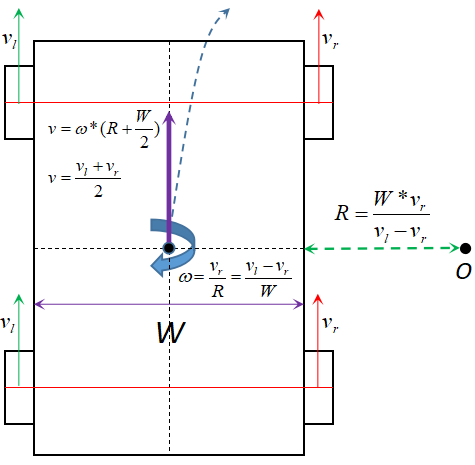
     滑移小车的运动方式为左侧两个轮子速度一致 \(v_l\)，右侧两个轮子的速度一致为 \(v_r\)，当小车需要向前运动时，\(v=v_l=v_r\) 即可实现小车的前向运动，当小车需要左转时，小车的右轮速度大于左轮速度\(v=\frac{v_r+v_l}{2}, \omega=\frac{v_r-v_l}{W}\)；当小车需要右转时，小车的左轮速度大于右轮速度\(v=\frac{v_r+v_l}{2}, \omega=\frac{v_l-v_r}{W}\)；由于在转动过程中会出现小车车轮滑动的情况，因此称为滑移式小车模型。
     在运动的过程中由于车轮相对于地面存在滑动，由于在实际环境中路面的摩擦力以及平整度的不同，导致小车整体的滑动方向是随机的，对于运动过程的控制就需要进行实时控制和跟踪。

二、阿克曼车体运动学模型

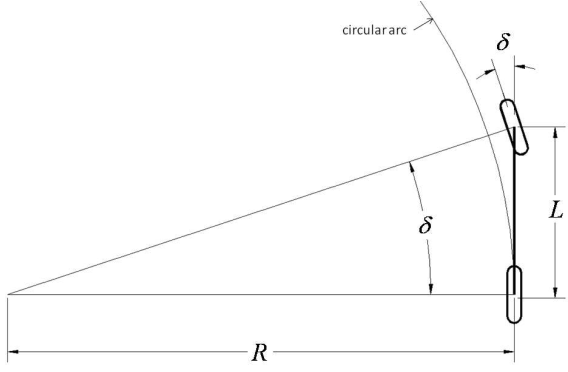
     阿克曼转向和自行车模型运动学的详细讨论。出于几何路径跟踪的目的，只需要说明自行车模型通过将两个前轮组合在一起和两个后轮组合在一起来简化四轮车，以形成两轮模型，就像自行车一样。第二个简化是车辆只能在平面上移动。这些简化导致前轮转向角和后轴将遵循的曲率之间的简单几何关系。

\[tan(\delta)=\frac{L}{R} \tag{1} \]

其中 \(δ\) 是前轮的转向角，\(L\) 是前轴和后轴之间的距离（轴距），\(R\) 是后轴在给定转向角下沿着行驶的圆的半径。该模型相当好地近似了汽车在低速和中等转向角下的运动。

Reference

1. 《Automatic_Steering_Methods_for_Autonomous_Automobile_Path_Tracking》 ⭐⭐⭐⭐⭐⭐
2. 规划控制之常用控制方法简介

1. 纯追踪方式的轨迹跟踪

I. 基础原理分析

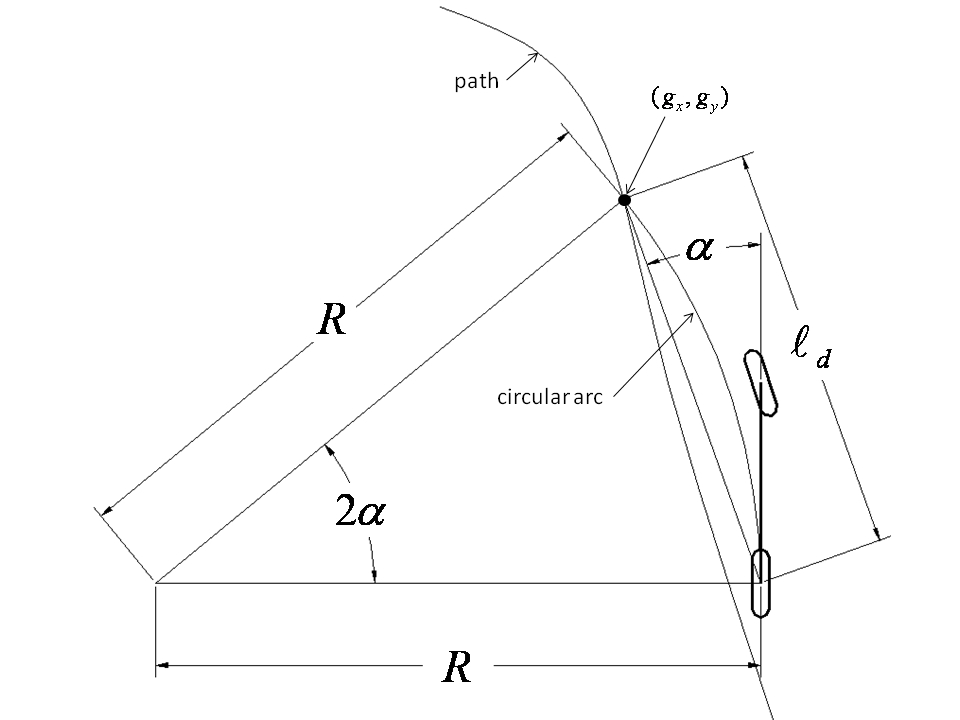
     纯追踪法包括几何计算连接后轴位置和车辆前方路径上目标点的圆弧的曲率。目标点由传感器确定。从当前后轴位置到期望路径的前进距离\(l_d\)。目标点 \((g_x,g_y)\) 。车辆的转向角 \(δ\) 可以仅使用目标点位置和车辆航向矢量与外观之间的角度 \(α\) 来确定。

\[\frac{l_d}{sin(2\alpha)}=\frac{R}{sin(\frac{\pi}{2}-\alpha)} \rArr \frac{l_d}{sin(\alpha)}=2R \rArr \kappa=\frac{2sin(\alpha)}{l_d} \tag{2} \]

将式(1) 带入式(2) 中可得：

\[\delta=tan^{-1}(\kappa L) \rArr \delta(t)=tan^{-1}(\frac{2Lsin(\alpha(t))}{l_d}) \tag{3} \]

II. 优势劣势

1. 前视距离变短，那么控制精度越高，但车辆控制会不稳定甚至震荡；
2. 前视距离越长，那么控制效果趋于平滑，震荡减弱，但又会出现车辆在某些急剧的转角处，转向不足的问题。
3. 曲率curvature（曲率半径R）对pure pursuit效果影响很大，某个曲率下，给定的pure模型可能工作的很好，在另一个曲率下，工作效果会突然变差，这是因为pure仅仅考虑了曲率，所以对curvature的依赖性就很强，并且这种效果会随着车速的增加越发增强。
4. 虽然可以缩小车辆与期望轨迹的位置偏差，但对角度偏差束手无策，因为数学原理上根本就没有考虑角度偏差。

适合直线多、弯道少、精度不太高的低速场景。

2. 斯坦利方法的轨迹跟踪

I. 基础原理分析

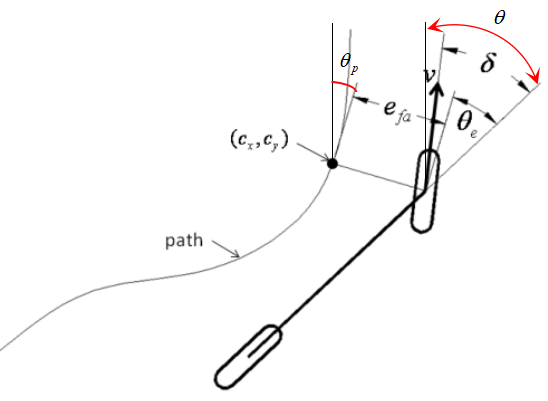
Stanley方法是斯坦福大学的自动驾驶汽车参赛项目在DARPA Grand Challenge，Stanley中使用的路径跟踪方法。Stanley方法是交叉轨迹误差efa的非线性反馈函数，从前轴中心到最近路径点 \((cx,cy)\) 测量，可以显示指数收敛。

\[\theta_e=\theta - \theta_p \]

上图示出了控制参数的几何关系。由此产生的转向控制律被给出为：

\[\delta(t)=\theta_e(t)+tan^{-1}(\frac{k\cdot e_{fa}(t)}{v_x(t)}) \]

Reference

1. 基于运动学约束的轨迹跟踪算法（Pursuit法，Stanley法）

3. 基于运动学模型的轨迹跟踪分析

     将车辆系统模型简化为运动学自行车模型是用于机器人运动规划、简单车辆分析和（与几何方法一样）导出直观的控制律。本章介绍了这种模型的运动学方程。此外，应用链式系统控制理论中的一种重要方法，重新建立了运动方程，并给出了路径跟踪的求解方法该理论的应用导致使用众所周知的控制理论工具来设计控制器和稳定性分析的能力。

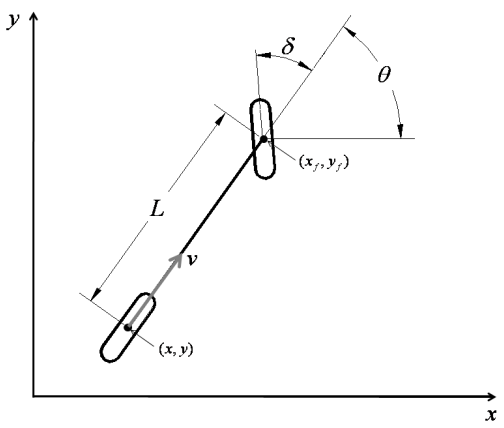
     为了完整起见，这里包括了模型的推导过程。运动自行车模型将左右轮在前轴和后轴的中心处折叠成一对单个车轮，如图18所示。假设车轮没有横向滑动，只有前轮是可转向的。将模型限制为在平面内运动，前轮和后轮的非完整约束方程为：

\[\frac{\dot{x_f}}{cos(\theta + \delta)} = \frac{\dot{y_f}}{sin(\theta + \delta)} \\ \frac{\dot{x}}{cos(\theta)} = \frac{\dot{y}}{sin(\theta)} \tag{1} \]

其中 \(\dot{x_f}\) 为前轮 \(x\) 方向的速度分量，\(\dot{x}\) 为后轮 \(x\) 方向的速度分量，\((x，y)\) 是后轮的全局坐标，\((x_f,y_f)\)是前轮的全局坐标，\(θ\) 是车辆在全局坐标系中的方位，\(δ\) 是车身坐标系中的转向角。由于前轮沿着车辆的方位位于距后轮沿着的距离 \(L\) 处，因此 \((x_f,y_f)\) 可以表示为:

\[x_f = x + L* cos(\theta) \rArr \dot{x_f}=\dot{x} - Lsin(\theta)\dot{\theta} \\ y_f = y + L* sin(\theta) \rArr \dot{y_f}=\dot{y} + Lcos(\theta)\dot{\theta} \tag{2} \]

将式（2）带入式（1） 中可以得到：

\[0=\dot{x}sin(\theta + \delta) - \dot{y} cos(\theta + \delta) - \dot{\theta}Lcos(\delta) \tag{3} \]

考虑车辆合速度与分速度之间的关系，具体如下：

\[\dot{x}=vcos(\theta) \\ \dot{y}=vsin(\theta) \tag{4} \]

将式（4）代入式（3）中可知：

\[\dot{\theta}=\frac{\dot{x}sin(\theta + \delta) - \dot{y} cos(\theta + \delta)}{Lcos(\delta)}=\frac{vtan(\delta)}{L} \tag{5} \]

由 \(v\) 和 \(θ\) 确定的车辆瞬时曲率半径 \(R\) 得出前面介绍的等式。

\[R=\frac{v}{\dot{\theta}}\\ \frac{vtan{(\delta)}}{L}=\frac{v}{R} \\ tan(\delta)=\frac{L}{R} \]

为了控制的目的，将来自方程8、9和10的运动学模型写成双输入无漂移形式是有用的:

\[ \]

Reference

1. 阿克曼车体模型

   • 汽车转向角度和转向半径的关系
   • 汽车在转向时两个转向轮的偏转角度不一样，这是正常的吗？
   • 前轮在转向时两个轮子的转动角度是完全一致的吗？
   • 阿克曼角
   • 麦克纳姆轮全向移动原理
   • 路径跟踪方案-参考论文
   • 自动泊车系统控制-参考论文

2. 通用机器人参考

   • 轮式机器人底板公司
   • 宇树机器人论坛
   • isaac Nvidia 文档翻译

3. 滑移转向车模型