PID算法简单剖析如下:
1、首先我们来看一下PID系统的基本组成模块:
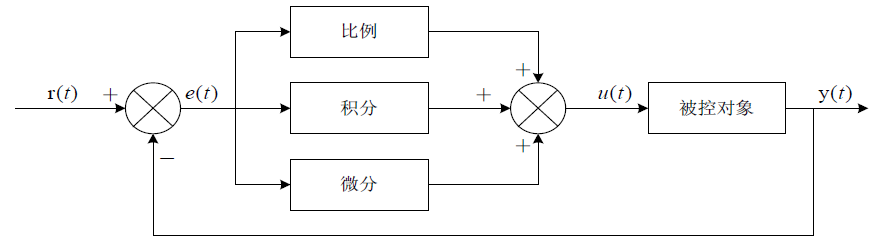
如图所示,图中相关参数的表示如下:
r(t):系统实际上需要的输出值,这是一个标准值,在我们设定了之后让这个系统去逼近的一个值(随时间变化的原因是,我们对系统的需求不同才会改变!)
y(t):系统当前的输出值,这个值应该需要趋近于我们设定的值,当我们没有增加PID控制模块之前,它是由被控对象通过r(t)输入直接产生的。
e(t):系统由于某些扰动,导致的系统产生的偏差,实际输出的值和想要设定的初始值r(t)的差值。
u(t):系统通过PID控制器输出的新的输入值,实际上他是在r(t)的基础上,针对当前的实际情况做出的改变。
Kp比例模块:系统PID比例因子,Kp能够对于产生的偏差e(t)能够迅速的作出反应,减少偏差。
Ki积分模块:系统PID积分因子,Ki能够用于消除静差,由于前面的误差有正有负,所以当前偏差的加入能够抵消部分,保持系统的稳定性,让系统有记忆功能。
Kd微分模块:系统微分因子,Kd能够体现出当前误差的变化趋势,引入有效早期修正信号,从而加快系统的动作速度,减少调节时间。
图中所示的信号关系公式如下所示:
信号误差公式:![]()
模拟信号的PID控制器公式: ![]()
离散信号的PID控制器公式:![]()
被控对象的信号公式:![]() (简单的线性系统,比如电机的PWM调速系统)
(简单的线性系统,比如电机的PWM调速系统)
上述公式参数描述:
Kp控制器比例系数、Ti控制器积分时间(积分系数)、Td控制器微分时间(微分系数)
k采样序列号,k=0,1,2,3...、Uk第k次采样时刻系统输出值、ek第k次采样时刻偏差值、ek-1第k-1次采样时刻偏差值、Ki=Kp*T/Ti、Kd=Kp*Td/T
2、离散信号的PID控制器算法仿真:
1、位置式PID算法:
![]()
PID系统产生的值,完全作为系统的输入参数,即采用u(k)代替了r(k),如果计算机出现故障时,位置式PID控制将导致Uk的剧烈变化,这会引起执行机构的大幅度变化,造成巨大损失。
仿真代码如下(python):
import matplotlib.pyplot as plt import numpy as np import random import sys import os time_length = 600 time_sample = 100 time_interval = float(time_length/time_sample) error_coeff = 3 t = np.linspace(0,time_length,time_sample) Slope = 1 Intercept = 0 standard_in = 20 # The system model system_model = lambda i : Slope*i + Intercept standard_out = system_model(standard_in) print("The Standard Output:%d" % standard_out) Kp = 0.08 # average Ki = -0.7 # intergre Kd = 0.01 # diff error_bef = [] real_out_ajust = [] real_out_ajust.append(70) real_out_ajust.append(75) error_bef.append(real_out_ajust[0]-standard_out) Out_plt = np.linspace(standard_out,standard_out,time_sample) # 标准直接计算公式1:Pout=Kp*e(t) + Ki*Sum[e(t)] + Kd*[e(t) - e(t-1)] def PID_Controller_Direct_Mem(standard_out,t): global time_sample,Kp,Ki,Kd,error_bef,real_out_ajust if t > time_sample: print("Time Out! Quit!") return -1 error_now = real_out_ajust[t] - standard_out error_bef.append(error_now) # 记录了所有的误差 integrate_res = np.sum(error_bef) Diffirent_res = error_now - error_bef[t-1] return Kp*error_now + Ki*integrate_res + Kd*Diffirent_res for t_slice in range(1,time_sample-1): Pout = PID_Controller_Direct_Mem(standard_out,t_slice) real_out_ajust.append(system_model(Pout)) plt.figure('PID_Controller_Direct_Mem') plt.xlim(0,time_length) plt.ylim(0,2*standard_out) plt.plot(t,real_out_ajust) plt.plot(t,Out_plt)
仿真结果如下所示:
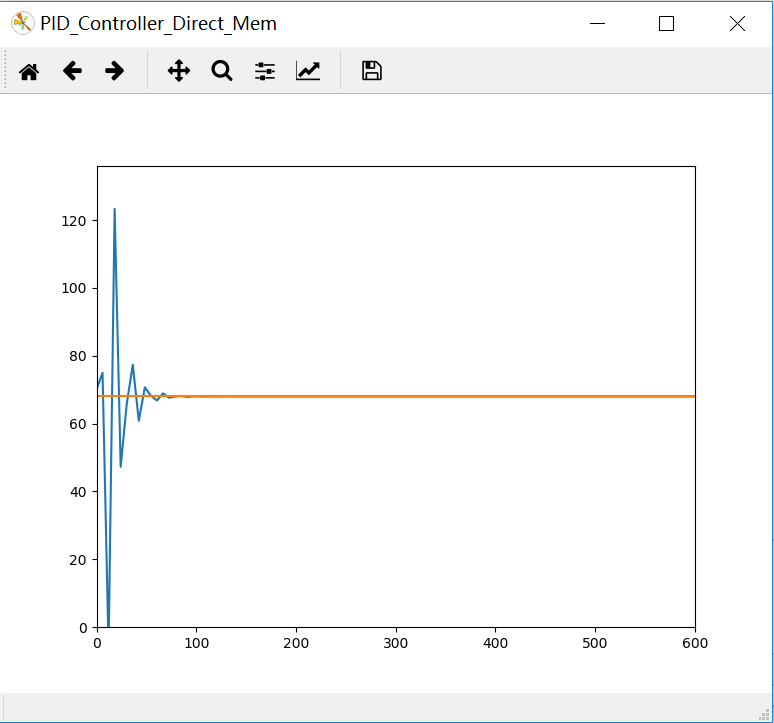 图中所示,系统最终收敛于我们设定的红线的位置r(t)
图中所示,系统最终收敛于我们设定的红线的位置r(t)
2、增量式PID算法:
![]()
当执行机构需要的控制量是增量而不是位置量的绝对数值是,可以采用增量式PID控制算法。
代码如下(python):
import matplotlib.pyplot as plt import numpy as np import random import sys import os class PID_Prama: def __init__(self): self.Kp = 0 self.Ki = 0 self.Kd = 0 self.set_val = 0 self.error_last = 0 self.error_prev = 0 self.error_sum = 0 # 增量计算公式: # Pout=Kp*[e(t) - e(t-1)] + Ki*e(t) + Kd*[e(t) - 2*e(t-1) +e(t-2)] def PID_Controller_Increa(pid,out_now): error = pid.set_val - out_now Res = pid.Kp*(error-pid.error_last) + pid.Ki*error + \ pid.Kd*(error-2*pid.error_last+pid.error_prev) pid.error_prev = pid.error_last pid.error_last = error return Res standard_out = 100 PID_val = PID_Prama() # PID参数 PID_val.Kp = 0.01 PID_val.Ki = 0.1 PID_val.Kd = 0.05 PID_val.set_val = standard_out # 标准输出值 # 增量型PID控制器输出值 PID_Controller_Increa_Out = [] Sys_In = [] # 0时刻系统输入值 Sys_In.append(5) # 系统响应函数 SystemFunc = lambda x : 5*x + np.random.normal(0,0.5,1)[0] Sys_Out = [] # 0时刻系统输出值 Sys_Out.append(SystemFunc(Sys_In[0])) for t_slice in range(Time): Diff = PID_Controller_Increa(PID_val,Sys_Out[t_slice]) #系统误差 PID_Controller_Increa_Out.append(Diff) # 记录所有的系统误差 Sys_In.append(Sys_In[0]+np.sum(PID_Controller_Increa_Out)) # 计算增量之后的新的系统输入 Sys_Out.append(SystemFunc(Sys_In[t_slice+1])) # 计算下一时刻系统新的输出值 standard = np.linspace(PID_val.set_val,PID_val.set_val,Time) plt.figure('PID_Controller_Increa') plt.xlim(0,Time) plt.ylim(0,2*standard_out) plt.plot(Sys_Out) plt.plot(standard) plt.show()
这里对增量式PID算法进行深入的分析和计算:
No1:class PID_Param类保存了PID算法中的三个参数,Kp Ki Kd,同时类当中也记录了上一次系统存在的误差error_last,以及上上一次系统的误差error_prev,这样就能够完成增量式误差的公式计算。
No2:上述算法中在循环体中记录了所有的误差变量PID_Controller_Increa_Out,这是为了仿真的目的,实际上我们比不需要存储所有的误差参数。
No3:系统的响应system_model:![]() ,系统后面添加了高斯噪声,这表示了系统在运行过程中的不稳定的过程,同时系统本身是一个线性系统,例如控制电机转速的系统:PWM--ctl--Speed
,系统后面添加了高斯噪声,这表示了系统在运行过程中的不稳定的过程,同时系统本身是一个线性系统,例如控制电机转速的系统:PWM--ctl--Speed
系统仿真结果:
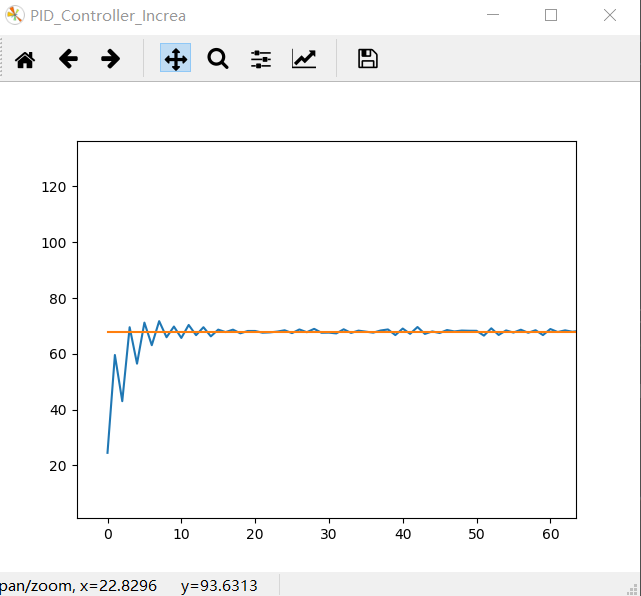
- 算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关,容易通过加权处理获得比较好的控制效果;
- 计算机每次只输出控制增量,即对应执行机构位置的变化量,故机器发生故障时影响范围小、不会严重影响生产过程;
- 手动—自动切换时冲击小。当控制从手动向自动切换时,可以作到无扰动切换
MATLAB仿真
https://blog.csdn.net/weixin_44044411/article/details/85891109
其他的相关参考资料见我的cnblog文件中,下一篇介绍PID实战,基于STM32微控制器的C语言控制PWM电机转速+力矩调节系统!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号