子序列

【模板】最长公共子序列

题目描述

给出 \(1,2,\ldots,n\) 的两个排列 \(P_1\) 和 \(P_2\) ，求它们的最长公共子序列。

输入格式

第一行是一个数 \(n\)。

接下来两行，每行为 \(n\) 个数，为自然数 \(1,2,\ldots,n\) 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

样例 #1

样例输入 #1

5 
3 2 1 4 5
1 2 3 4 5

样例输出 #1

3

提示

• 对于 \(50\%\) 的数据， \(n \le 10^3\)；
• 对于 \(100\%\) 的数据， \(n \le 10^5\)。

AC

点击查看代码

const int maxn = 1e5 + 10;
int a[maxn], b[maxn];
void solve() {
    int n;
    cin >> n;
    map<int, int> ma;//ai在a的位置
    for (int i = 2; i <= n; i++) {
        cin >> a[i];
        ma[a[i]] = i;
    }
    for (int i = 2; i <= n; i++) {
        cin >> b[i];
    }
    vector<int> dp(maxn, 0);
    // dp记长度i为公共序列的最后一个数在a的位置
    dp[1]   = ma[b[1]];
    int len = 1;
    for (int i = 2; i <= n; i++) {
        int id = ma[b[i]];
        // id在序列之后/直接加入
        if (id > dp[len]) { dp[++len] = id; }
        // 之前/利用二分更新最小的位置
        else {
            int l = 1, r = len, res = 1;
            while (l <= r) {
                int mid = (l + r) >> 1;
                if (dp[mid] > id) {
                    r   = mid - 1;
                    res = mid;
                }
                else { l = mid + 1; }
            }
            dp[res] = id;
        }
    }
    cout << len;
}

对于最长上升子序列（LIS）类问题

n²

点击查看代码

for(int i=1;i<=n;i++)
	{
		dp[i]=1;//初始化
		for(int j=1;j<i;j++)//枚举i之前的每一个j
		if(data[j]<data[i] && dp[i]<dp[j]+1)
		//用if判断是否可以拼凑成上升子序列，
		//并且判断当前状态是否优于之前枚举
		//过的所有状态,如果是，则
		dp[i]=dp[j]+1;//更新最优状态
	}

nlogn

点击查看代码

for(int i=2;i<=n;i++)
	{
		int l=0,r=len,mid;
		if(a[i]>f[len])f[++len]=a[i];
		//如果刚好大于末尾，暂时向后顺次填充 
		else 
		{
		while(l<r)
		{	
		    mid=(l+r)/2;
		    if(f[mid]>a[i])r=mid;
	//如果仍然小于之前所记录的最小末尾，那么不断
	//向前寻找(因为是最长上升子序列，所以f数组必
	//然满足单调) 
			else l=mid+1; 
		}
		f[l]=min(a[i],f[l]);//更新最小末尾 
     	}
    }

对于最长公共子序列（LCS）问题，如本题

n²

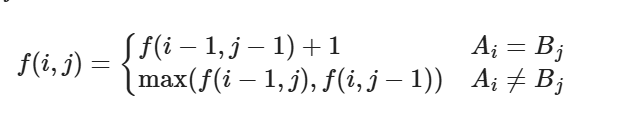
nlogn

利用map对a数组位置标记，看做b数组在寻找公共子序列的权（大小）
//大的尽量放在小的后面
将其等价做LIS问题