leetcode190. 颠倒二进制位

190. 颠倒二进制位

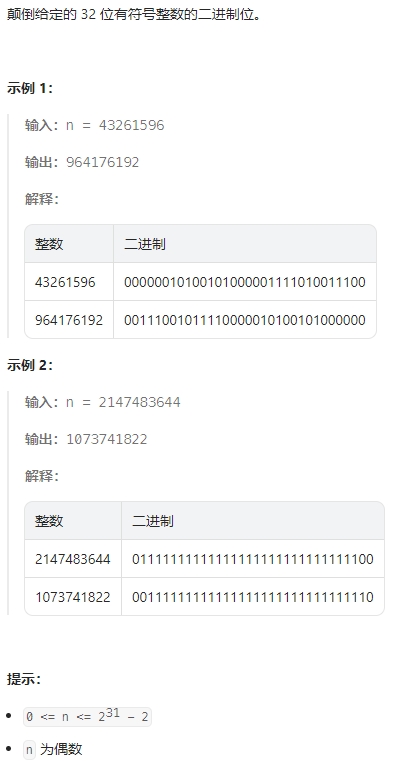
注意，如果n转成二进制不够32位，要在最高位前面补0再反转

法一：自己写的，不太高效，return那的复杂度太高了

class Solution {
    public int reverseBits(int n) {
        StringBuilder sb = new StringBuilder();
        int count = 0;
        while(n > 0){
            char c = (n & 1) == 1 ? '1' : '0';
            sb.append(c);
            n >>= 1;++count;
        }
        while((count++) < 32)  sb.append('0');
        return Integer.parseInt(sb.toString(),2);
    }
}

 法二：逐位颠倒

在第一次循环时，rev为 0，执行 rev <<= 1后它确实还是 0。这个操作在第一次循环中看似多余，但却是整个算法能够严丝合缝工作的关键。它建立了一个固定且可靠的节奏，确保从第二位开始，每一位都能被准确地放置到正确的位置。

核心原理：为下一位腾出位置

你可以把 rev变量想象成一个正在从右向左组装的二进制数。rev <<= 1这个操作的核心目的，永远是为即将到来的新位（来自原始数字 n的最低位）在 rev的最右侧腾出一个空位（即最低位）。这个固定的节奏——“先移位腾空位，再填充新位”——保证了整个过程的一致性。

假设我们要反转一个4位的数字 1101(十进制13)，目标是得到 1011(十进制11)。下表一步步展示了在循环中 rev <<= 1所起的关键作用：

循环次数 (i)	操作前 n的二进制	操作前 rev的二进制	操作1: rev <<= 1(为新位腾空)​	**操作2: `rev	= (n & 1)` (填充新位)**​	操作3: n >>>= 1(准备下一位)
初始​	1101	0000	-	-	-
第1次​	1101	0000	0000 << 1 = **0000**(腾出的位是0)	`0000	1 = 0001`	1101 >>> 1 = 0110
第2次​	0110	0001	0001 << 1 = **0010**(为下次填充腾出最低位0)	`0010	0 = 0010`	0110 >>> 1 = 0011
第3次​	0011	0010	0010 << 1 = **0100**(腾出最低位0)	`0100	1 = 0101`	0011 >>> 1 = 0001
第4次​	0001	0101	0101 << 1 = **1010**(腾出最低位0)	`1010	1 = 1011`	0001 >>> 1 = 0000

class Solution {
    public int reverseBits(int n) {
        int rev = 0;//可以把 rev变量想象成一个正在从右向左组装的二进制数。
        for (int i = 0; i < 32; i++) {
            rev <<= 1;  // 1.这个操作的核心目的，永远是为即将到来的新位（来自原始数字 n的最低位）在 rev的最右侧腾出一个空位（即最低位）。
            
            if ((n & 1) == 1)  rev |= 1;  // 2. 如果n的最低位是1，则将rev的最低位也设为1
            
            // 3. n右移一位，处理下一位
            n >>>= 1; // 使用无符号右移，确保高位补0
        }
        return rev;
    }
}

 法三：位运算分治

public class Solution {
    // 定义掩码常量，用于分组操作
    private static final int M1 = 0x55555555; // 01010101010101010101010101010101 (用于交换相邻的1位)
    private static final int M2 = 0x33333333; // 00110011001100110011001100110011 (用于交换相邻的2位)
    private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111 (用于交换相邻的4位)
    private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111 (用于交换相邻的8位)

    public int reverseBits(int n) {
        // 第一步：交换相邻的1位（奇偶位交换）
        // 将原始二进制序列中相邻的两个比特位进行交换
        n = n >>> 1 & M1 | (n & M1) << 1;
        
        // 第二步：交换相邻的2位
        // 将第一步结果中每相邻的两对比特位（共4位）进行交换
        n = ((n >>> 2) & M2) | ((n & M2) << 2);
        
        // 第三步：交换相邻的4位（即交换字节中的高低4位）
        // 将第二步结果中每相邻的两组4位（共8位）进行交换
        n = n >>> 4 & M4 | (n & M4) << 4;
        
        // 第四步：交换相邻的8位（即交换16位中的高低字节）
        // 将第三步结果中每相邻的两个字节（共16位）进行交换
        n = ((n >>> 8) & M8) | ((n & M8) << 8);
        
        // 第五步：交换高低16位（完成最终颠倒）
        // 将整个32位二进制数的高16位和低16位进行交换
        return n >>> 16 | n << 16;
    }
}

下面的表格展示了整个分治过程中二进制位是如何一步步被颠倒的：

步骤	操作描述	交换粒度	示例（32位）	掩码作用
初始状态​	原始二进制序列	-	abcdefgh ijklmnop qrstuvwx yzABCDEF	-
第一步后​	交换相邻的1位​	每1位交换	badcfehg jilknmpo rsqutvwy xAzBCEDF	M1隔离奇数位和偶数位
第二步后​	交换相邻的2位​	每2位交换	dcbahgfe lkjipomn vutsrqyx wAzFEDCB	M2隔离每2位一组
第三步后​	交换相邻的4位​	每4位交换	hgfedcba ponmlkji yxwvutsr FEDCBAzy	M4隔离每4位（半字节）
第四步后​	交换相邻的8位​	每8位（字节）交换	ponmlkji hgfedcba FEDCBAzy yxwvutsr	M8隔离每8位（字节）
第五步后​	交换高低16位​	整个字交换	FEDCBAzy yxwvutsr ponmlkji hgfedcba	完成最终颠倒

掩码的关键作用：每个掩码（M1, M2, M4, M8）都是一个位掩码（Bit Mask），其二进制模式由交替的0和1组成。它们的主要作用是在移位操作时保留需要的位，清除不需要的位，防止不同组之间的位在移位时相互干扰。

假设我们聚焦于一个4位的单元 ABCD（其中A、B、C、D各代表1个比特），我们的目标是将其交换为 CDAB。整个过程如下表所示：

步骤	操作	二进制结果（以4位单元 ABCD为例）	解释
1. 初始状态​	-	A B C D	我们的目标是将AB和CD的位置互换。
2. 取出“偶数组” (CD)​	n >>> 2	0 0 A B	将整个数无符号右移2位。
3. 屏蔽无关位​	(n >>> 2) & M2	0 0 A B	用 M2（二进制0011）进行按位与。
4. 取出“奇数组” (AB)​	n & M2	0 0 C D	得到后一对比特
5. 移动“奇数组”​	(n & M2) << 2	C D 0 0	将取出的 C和 D左移2位。
6. 合并结果​	前两步结果相或 (...)\|(...)	C D A B	将第3步的结果（0 0 A B）和第5步的结果（C D 0 0）进行按位或运算。由于它们的位置是错开的，0与任何值或都是该值本身，所以完美地拼接成了 CDAB，完成了交换。

经过以上六步，我们就成功地交换了相邻的两对比特位（共4位）。这个精妙的过程利用了掩码的隔离、位移的移动和按位或的合并，是分治思想在位运算中的典型体现。