leetcode73. 矩阵置零

73. 矩阵置零

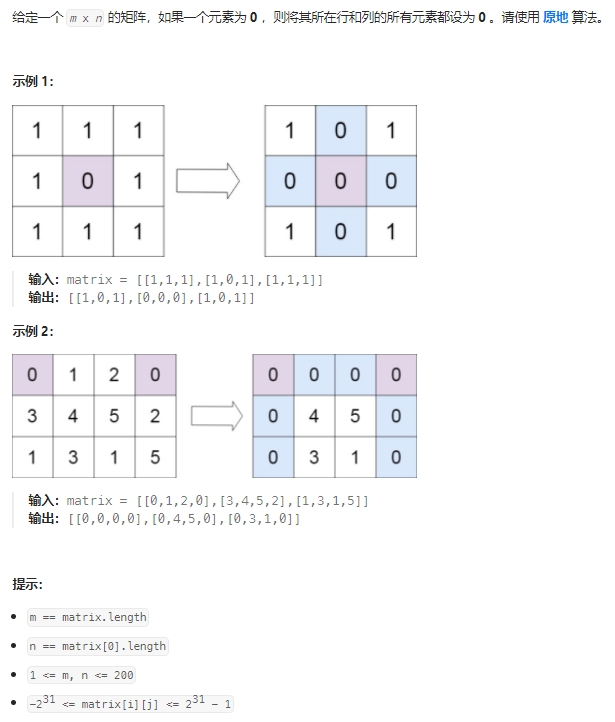
法一：和零的数量相关的额外数组

202209写的c++代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int size1=matrix.size(),size2=matrix[0].size();
        vector<vector<int>> zero;
        for(int i=0;i<size1;i++)
        {
            for(int j=0;j<size2;j++)
            {
                if(matrix[i][j]==0) zero.push_back({i,j});
            }
        }
        int sizezero=zero.size();
        for(int i=0;i<sizezero;i++)
        {
            int m=zero[i][0],n=zero[i][1];
            for(int j=0;j<size2;j++)
            {
                matrix[m][j]=0;
            }
            for(int j=0;j<size1;j++)
            {
                matrix[j][n]=0;
            }
        }
    }
};

202511写的java代码

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length,n = matrix[0].length;
        ArrayList<Integer> mZero = new ArrayList<>();
        ArrayList<Integer> nZero = new ArrayList<>();
        for(int i = 0;i < m;++i){
            for(int j = 0;j < n;++j){
                if(matrix[i][j] == 0){
                    mZero.add(i);nZero.add(j);
                }
            }
        }
        int size = mZero.size();
        for(int i = 0;i < size;++i){
            for(int j = 0;j < n;++j){
                matrix[mZero.get(i)][j] = 0;
            }
        }
        for(int i = 0;i < size;++i){
            for(int j = 0;j < m;++j){
                matrix[j][nZero.get(i)] = 0;
            }
        }
    }
}

法二：不使用额外数组，用第一列作为标记

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length,n = matrix[0].length;
        boolean tagCol = false;// 标记第一列是否原本有0
        
        // 标记值为0的元素所在的行和列
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0)  tagCol = true;  // 标记第一列是否有0
            for (int j = 1; j < n; j++) {
                // 如果matrix[i][j]==0，则将该元素所在行和列的第一个元素设置为0
                if (matrix[i][j] == 0)  matrix[i][0] = matrix[0][j] = 0;
            }
        }
        
        // 矩阵元素置0：采用倒序遍历
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j > 0; j--) { // 注意j>0，不处理第一列
                if (matrix[i][0] == 0 || matrix[0][j] == 0)  matrix[i][j] = 0;
            }  
            if (tagCol)  matrix[i][0] = 0; // 第一列元素置零
        }
    }
}