matlab基础语法

基本语法

A = [1 2 3; 4 5 6;  8 4 9];
B = A';%求矩阵转置
C = A(:);%将矩阵逐列转为列向量
D = inv(A);%矩阵求转置
E = zeros(10,5,3);%生成元素全是0的10*5*3
E(:,:,1) = rand(10,5);%rand(m,n)生成m行n列均匀分布的伪随机数 %randn生成标准正态分布的伪随机数
E(:,:,2) = randi(5,10,5);%randi(iMax,m,n)在开区间(0,iMax)生成m*n随机矩阵
E(:,:,3) = rand(10,5);

F = cell(1,6);
F{2} = eye(3);%生成一个3*3的单位矩阵
F{5} = magic(5);%magic(n)生成一个n阶幻方，就是把1~n^2排成n*n矩阵，使得矩阵每行每列以及主副对角线上的n个数之和都相等

books = struct('name',{{'machine learning','data mining'}},'price',[30 40]);
books.name
books.name(1);%cell
books.name{1};%字符串

BB = 1:2:9;%BB = start:step:end %生成一个行向量，起始是start,结束是end,步长是step
CC = repmat(BB,3,4);%repmat(B,m,n) %先生成将行向量B重复n次的行向量，再将这个行向量在列的方向重复m次，生成一个新矩阵
DD = ones(3,4) %ones(m,n) %生成元素全为1的m*n的矩阵

EE = [1 2 3; 4 5 6; 8 4 9];
FF = [6,8,1; 7,3,4; 2,7,8];
GG = EE .* FF; %两个矩阵对应元素相乘
HH = EE / FF; %相当于 EE 乘 FF的逆
II = EE ./ FF; %两个矩阵对应元素相除 

AAA = magic(5);
BBB = AAA(2,3); %A(m,n) %取矩阵第m行第n列的元素
CCC = AAA(3,:); %A(m,:) %取矩阵第m个行向量
DDD = AAA(:,4); %A(:,n) %取矩阵第n个列向量
[m,n] = find(AAA > 20); %find(A > 20) %寻找矩阵中大于20的元素的下标，分别将行、列下标存储为两个列向量

基本的画图语法

%绘制二维平面
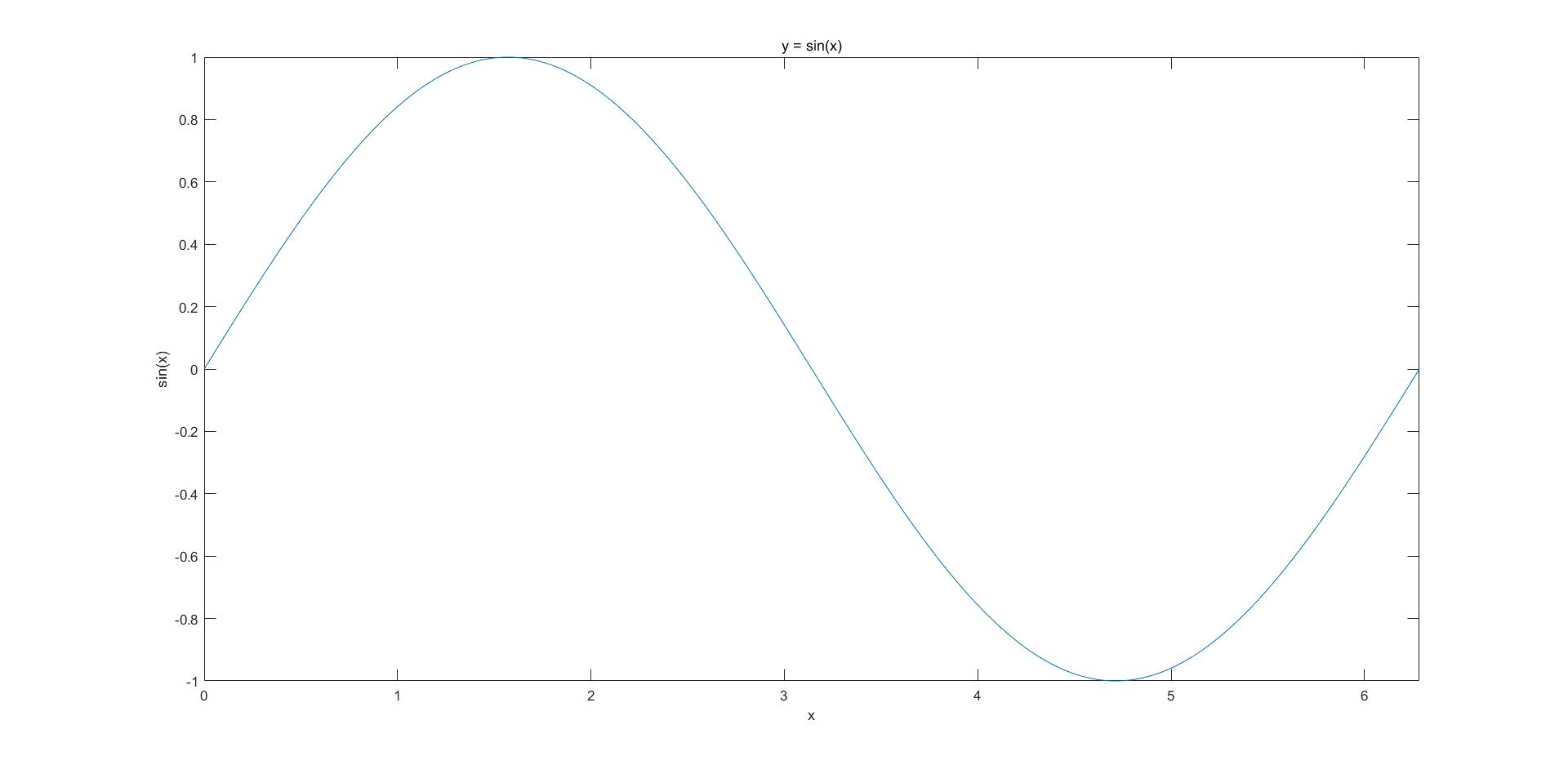
x = 0:0.01:4*pi;
y = sin(x)
figure %建立一个幕布
plot(x,y);
title('y = sin(x)');
xlabel('x');
ylabel('sin(x)');
xlim([0 2*pi]);

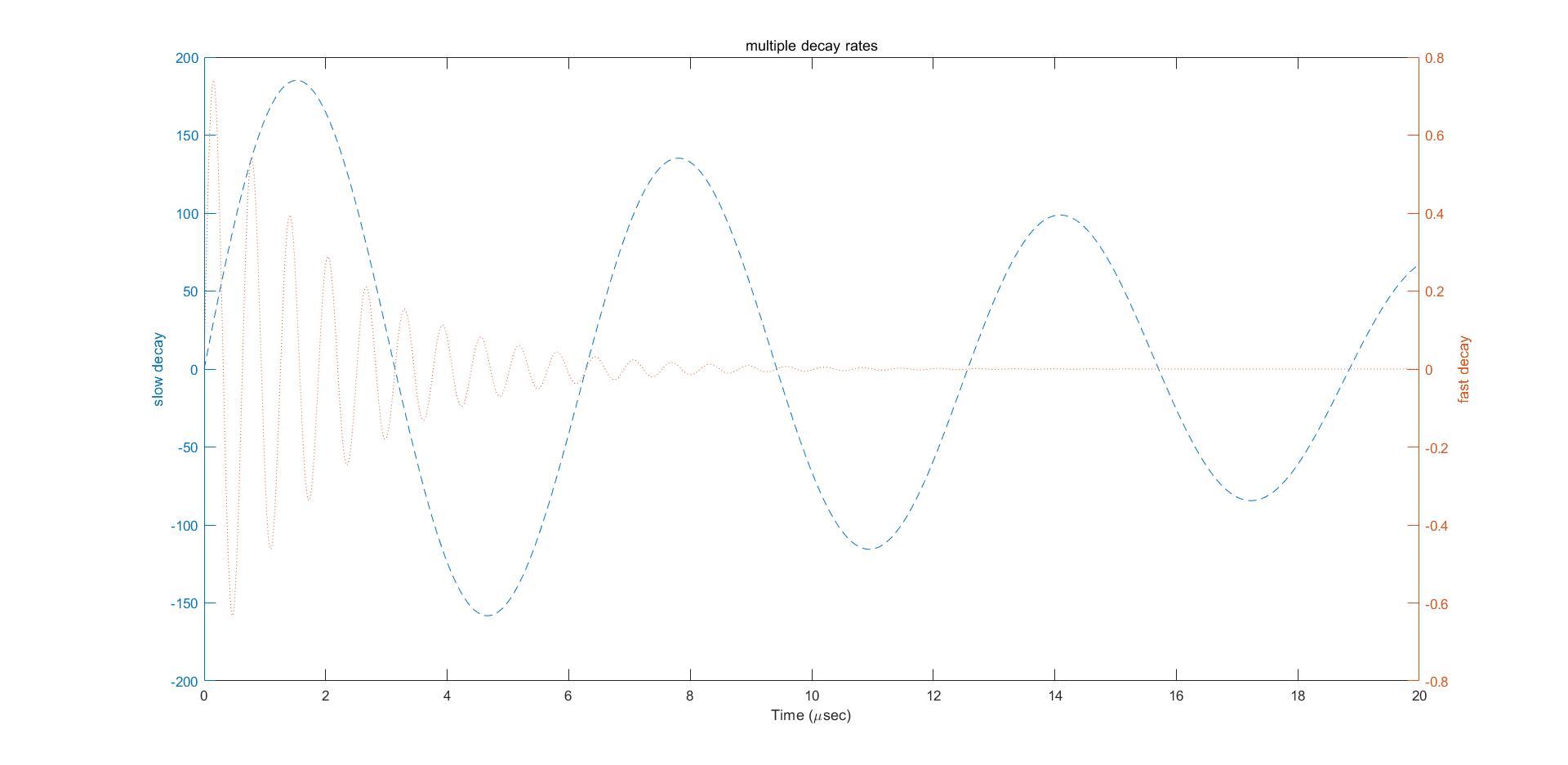
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x)
y2 = 0.8*exp(-0.5*x).*sin(10*x)
[AX,H1,H2] = plotyy(x,y1,x,y2,'plot');%plotyy是共用一个x坐标系，在y轴上有不同的取值
set(get(AX(1),'Ylabel'),'String','slow decay')
set(get(AX(2),'Ylabel'),'String','fast decay')
xlabel('Time (\musec)')
title('multiple decay rates')
set(H1,'LineStyle','--')
set(H2,'LineStyle',':')

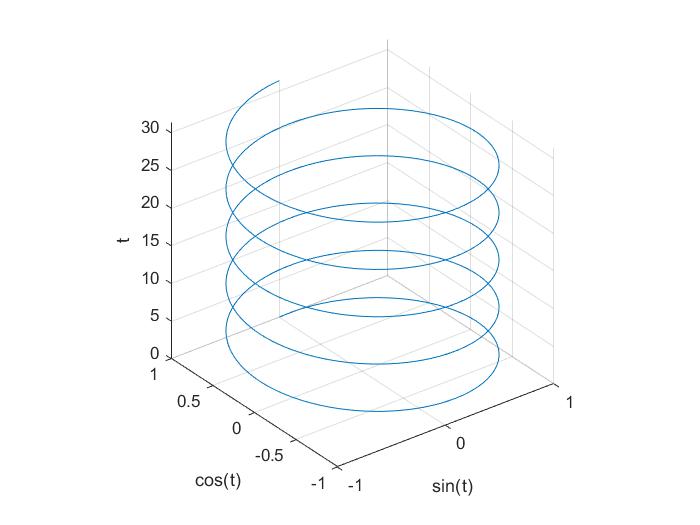
t = 0:pi/50:10*pi
plot3(sin(t),cos(t),t)
xlabel('sin(t)')
ylabel('cos(t)')
zlabel('t')
grid on %打开网格
axis square %使生成的三维图形是方形的

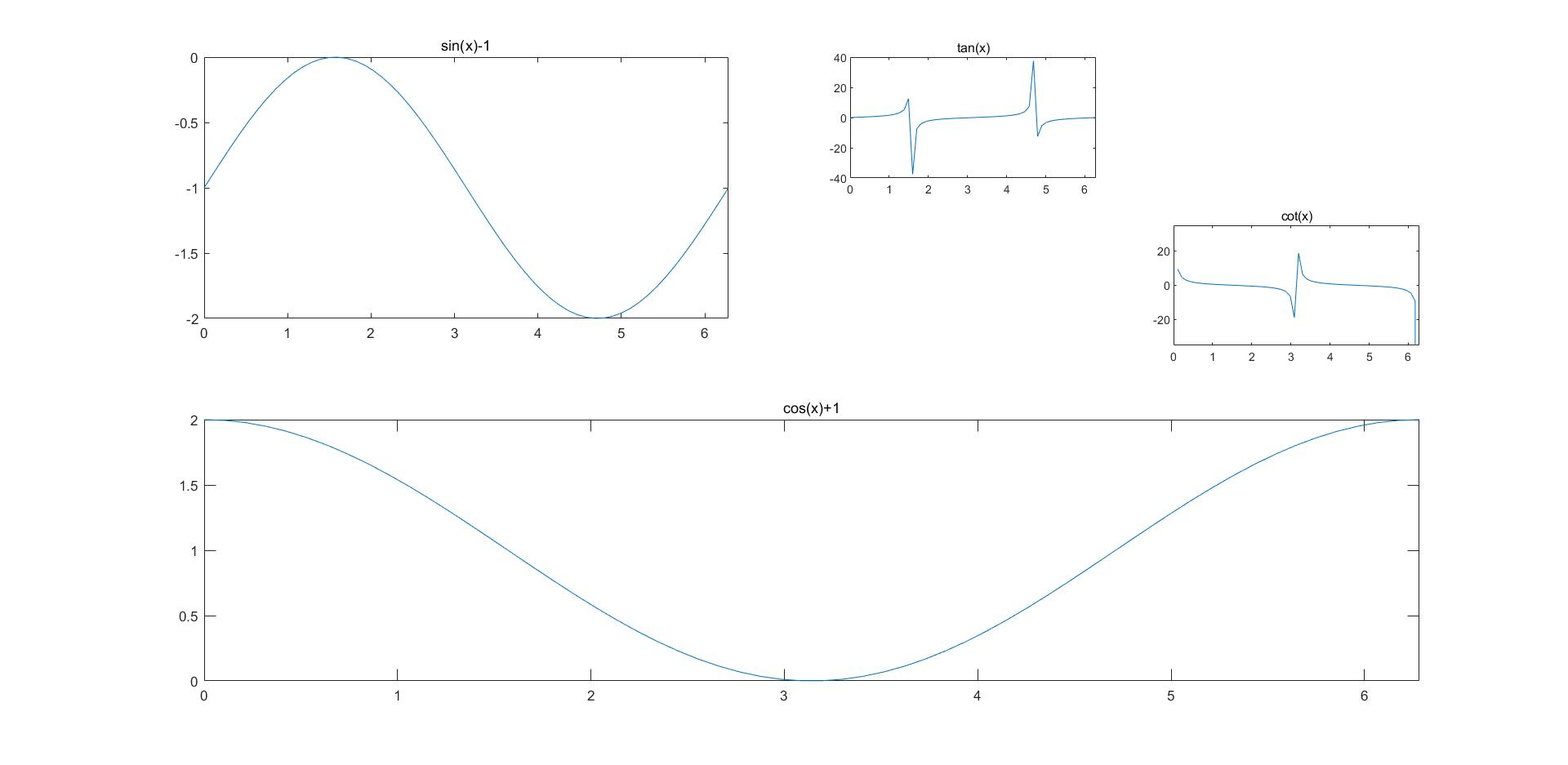
%subplot(m,n,p) %将幕布平均分成m*n，放在第p个位置
x = linspace(0,2*pi,60);
subplot(2,2,1);%将幕布平均分成2*2，放在第1个位置
plot(x,sin(x)-1);
title('sin(x)-1');
axis([0,2*pi,-2,0]);
subplot(2,1,2);%将幕布平均分成2*1，放在第2个位置
plot(x,cos(x)+1);
title('cos(x)+1');
axis([0,2*pi,0,2]);
subplot(4,4,3);%将幕布平均分成4*4，放在第3个位置
plot(x,tan(x));
title('tan(x)');
axis([0,2*pi,-40,40]);
subplot(4,4,8);%将幕布平均分成4*4，放在第8个位置
plot(x,cot(x));
title('cot(x)');
axis([0,2*pi,-35,35]);

常用运算符和特殊运算符

运算符	目的

*	标量和矩阵乘法运算符
.*	数组乘法运算符
^	标量和矩阵求幂运算符
.^	数组求幂运算符
\	矩阵左除
/	矩阵右除
.\	阵列左除
./	阵列右除
:	向量生成；子阵提取
( )	下标运算；参数定义
[ ]	矩阵生成
.	点乘运算，常与其他运算符联合使用
…	续行标志；行连续运算符
,	分行符（该行结果不显示）
;	语句结束；分行符（该行结果显示）
%	注释标志
_	引用符号和转置运算符
._	非共轭转置运算符
=	赋值运算符

特殊变量与常量

Name	Meaning
ans	默认的变量名，最近一次操作运算结果
eps	浮点数的相对误差
i,j	虚数单位，定义为 i²= j²= -1
Inf	代表无穷大
NaN	代表不定值（不是数字）
pi	圆周率

whos 命令则显示多一点有关变量：

当前内存中的变量
每个变量的类型
内存分配给每个变量
无论他们是复杂的变量与否

MATLAB格式命令

默认情况下，MATLAB 四个小数位值显示数字。这就是所谓的 short format.

如果想更精确，需要使用 format 命令。

长（long ） 命令格式显示小数点后16位。

例如：

format long
x = 7 + 10/3 + 5 ^ 1.2

MATLAB将执行上面的语句，并返回以下结果：

x =
  17.231981640639408

format short 例子：

format short
x = 7 + 10/3 + 5 ^ 1.2

MATLAB将执行上面的语句，并返回以下结果：

x =
   17.2320

空格格式命令回合到小数点后两位数字。例如：

format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6

MATLAB将执行上面的语句，并返回以下结果：

weekly_wage =
       1064.70

MATLAB 显示大量使用指数表示法。

短格式e命令允许以指数的形式显示小数点后四位，加上指数。

例如：

format short e
4.678 * 4.9

MATLAB将执行上面的语句，并返回以下结果：

ans =
   2.2922e+01

format long e命令允许以指数的形式显示小数点后十六位，加上指数。例如：

format long e
x = pi

MATLAB将执行上面的语句，并返回以下结果：

x =
     3.141592653589793e+00

format rat 命令给出由计算得出的最接近的有理表达式，从计算所得。例如：

format rat
4.678 * 4.9

MATLAB将执行上面的语句，并返回以下结果：

ans =
   2063/90

MATLAB创建向量

创建行向量括在方括号中的元素的集合，用空格或逗号分隔的元素。

例如，

r = [7 8 9 10 11]

创建列向量通过内附组方括号中的元素，使用分号（;)分隔的元素。

c = [7;  8;  9;  10; 11]

MATLAB switch语句语法

n = input('Enter a number: ');

switch n
    case -1
        disp('negative one')
    case 0
        disp('zero')
    case 1
        disp('positive one')
    otherwise
        disp('other value')
end

MATLAB while循环语法

a = 10;
% while loop execution 
while( a < 20 )
  fprintf('value of a: %d\n', a);
  a = a + 1;
end

MATLAB for 循环语法:

例1

for a = 10:20 
  fprintf('value of a: %d', a);
end

例2

for a = 1.0: -0.1: 0.0
   disp(a)
end

例3

for a = [24,18,17,23,28]
   disp(a)
end

MATLAB向量

引用向量元素

v = [ 1; 2; 3; 4; 5; 6];    % creating a column vector of 6 elements
v(3) %3

当引用一个冒号，一个向量，其例如为v（:)，该载体上的所有组件的被列出。

例如：

v = [ 1; 2; 3; 4; 5; 6];    % creating a column vector of 6 elements
v(:)

执行上述语句，返回下述结果：

MATLAB允许你选择一个范围从向量的元素。

在下面的例子中，我们创建了一个行向量rv 9个元素，我们将引用元素3至7写rv（3:7），并创建一个新的向量名为sub_rv。

rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)

MATLAB将执行上面的语句，并返回以下结果：

sub_rv =
     3     4     5     6     7

disp(C);
disp(D);  %disp可用于展示向量各个元素

MATLAB追加向量

MATLAB 允许在原有的向量中附加向量，共同创造新的向量。

如果有两个行向量 r1 和 r2 这两个行向量中各有 n 和 m 个元素，现在创建行向量 r 并将n和m个元素都放在行向量 r 中，通过附加这些载体，编写：

r = [r1,r2]

通过追加这两个向量，向量r2的，也可以建立一个矩阵R，矩阵的第二行编写如下：

r = [r1;r2]

要注意的是，要完成上述操作，上述两个载体中的元素的数量应该相同。

当然，可以附加两个列向量 c1 和 c2 的 n 和 m 的元素个数。要创建一个列向量 c 将 n 加 m 个元素放入其中，通过附加这些载体，编写：

c = [c1; c2]

还可以创建一个矩阵c追加这两个向量；向量c2将第二列的矩阵：

c = [c1, c2]

同样要注意，完成上述操作，上述两个载体中的元素的数量应该相同。

例

r1 = [ 1 2 3 4 ];
r2 = [5 6 7 8 ];
r = [r1,r2]
rMat = [r1;r2]
 
c1 = [ 1; 2; 3; 4 ];
c2 = [5; 6; 7; 8 ];
c = [c1; c2]
cMat = [c1,c2]

运行结果

r =
     1     2     3     4     5     6     7     8
rMat =
     1     2     3     4
     5     6     7     8
c =
     1
     2
     3
     4
     5
     6
     7
     8
cMat =
     1     5
     2     6
     3     7
     4     8

MATLAB向量的模

向量 v 中的元素 v1, v2, v3, …, vn，下式给出其幅度：

|v| = √(v1^2 + v2^2 + v3^2 + … + vn^2)

MATLAB中需要采按照下述步骤进行向量的模的计算：

采取的矢量及自身的积，使用数组相乘（*）。这将产生一个向量sv，其元素是向量的元素的平方和V.

sv = v.*v;
使用求和函数得到 v。这也被称为矢量的点积向量的元素的平方的总和V.

dp= sum(sv);
使用sqrt函数得到的总和的平方根，这也是该矢量的大小V.

mag = sqrt(s);

v = [1: 2: 20];
sv = v.* v;     %the vector with elements 
                % as square of v's elements
dp = sum(sv);    % sum of squares -- the dot product
mag = sqrt(dp);  % magnitude
disp('Magnitude:'); disp(mag);

结果

Magnitude:
   36.4692

MATLAB向量点积

MATLAB 中两个向量的点积 a = (a1, a2, …, an) and b = (b1, b2, …, bn) 由以下给定:

a.b = ∑(ai.bi)

下述函数可以计算两个向量 a 和 b 的点积：

dot(a, b);

详细例子

在MATLAB中建立一个脚本文件，代码如下：

v1 = [2 3 4];
v2 = [1 2 3];
dp = dot(v1, v2);
disp('Dot Product:'); disp(dp);

运行该文件，显示结果如下：

Dot Product:
    20

MATLAB矩阵

在MATLAB中创建矩阵有以下规则：

矩阵元素必须在 “[ ]” 内；
矩阵的同行元素之间用空格（或 “,”）隔开；
矩阵的行与行之间用 “;”（或回车符）隔开；
矩阵的元素可以是数值、变量、表达式或函数；
矩阵的尺寸不必预先定义。

MATLAB引用一个矩阵的元素

如果要引用 m^th 行和 n^th 列的一个元素，写法如下：

mx(m, n);

例如，参阅第2行和第5列中的元素的矩阵，所创建的最后一节中，我们输入：

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)

MATLAB将执行上述语句，并返回结果：

ans =
     6

引用m列中的所有元素，我们A型（m）。

接下来我们要从矩阵 a 的第4列的元素开始建立一个列向量 v ：

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)

MATLAB将执行上述语句，并返回结果：

当然也可以选择第 n 列的 m 个元素，对于这一点，写法如下：

a(:,m:n)

建立一个较小的子矩阵，取第m列到第n列，则 a(:, m:n)

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB将执行上述语句，并返回以下结果：

用相同的方式，则可以建立一个子矩阵的一个子部分的矩阵。

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

MATLAB将执行上述语句，并返回结果：

用相同的方式，则可以创建一个子矩阵的一个子部分的矩阵。

若使用矩阵A的第m~n行，第p~q列元素创建新矩阵，则为：A(m:n,p:q)

例如，让我们创建一个子矩阵内部子部分的：

3     4     5     
4     5     6

下述写法可以达到该目的：

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)

MATLAB将执行上述语句，并返回结果：

sa =
     3     4     5
     4     5     6

可以删除整行或整列的矩阵，只要分配一组空方括号 [ ] 给该行或列。

基本上，[ ] 表示一个空数组。

删除矩阵A的第m行，则为：A(m,:) = [ ]

在下述例子中我们删除第四行：

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []

MATLAB将执行上述语句，并返回结果：

a =
     1     2     3     4     5
     2     3     4     5     6
     3     4     5     6     7

接下来，我们删除第五列：

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]

MATLAB将执行上述语句，并返回结果：

a =
     1     2     3     4
     2     3     4     5
     3     4     5     6
     4     5     6     7

将矩阵A中的第m行和第n行复制两次，创建一个新矩阵，则为：A([m,n,m,n],:)

在本例中，我们会建立一个3-3的矩阵 m，并把矩阵 m 中的第二行和第三行复制两次，这样就能够建立一个4×3的矩阵。

在MATLAB中建立一个脚本文件，代码如下：

a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)

运行该文件，显示结果：

new_mat =
     4     5     6
     7     8     9
     4     5     6
     7     8     9

MATLAB串联矩阵

MATLAB中使用一对中括号“[ ]”，能够将两个矩阵连接起来，创建出一个新矩阵。

MATLAB串联矩阵的两种类型：

水平串联：要进行连接的两个矩阵是使用逗号 “,” 分隔开的。
垂直串联：要进行连接的两个矩阵是使用分号 “;” 分隔开的。

详细例子

在MATLAB中建立一个脚本文件，代码如下：

a = [ 10 12 23 ; 14 8 6; 27 8 9]
b = [ 12 31 45 ; 8 0 -9; 45 2 11]
c = [a, b]
d = [a; b]

运行该文件，显示结果：

a =
    10    12    23
    14     8     6
    27     8     9
b =
    12    31    45
     8     0    -9
    45     2    11
c =
    10    12    23    12    31    45
    14     8     6     8     0    -9
    27     8     9    45     2    11
d =
    10    12    23
    14     8     6
    27     8     9
    12    31    45
     8     0    -9
    45     2    11

MATLAB矩阵的行列式

MATLAB要计算对应矩阵行列式的值的指令为：d=det(A)，该指令返回矩阵 A 的行列式，并把所得值赋给 d。若 A 仅包含整数项，则该结果 d 也是一个整数。

详细例子

在MATLAB中建立一个脚本文件，代码如下：

a = [ 1 2 3; 2 3 4; 1 2 5]
det(a)

运行该文件，显示以下结果：

a =
     1     2     3
     2     3     4
     1     2     5
ans =
    -2

MATLAB逆矩阵

MATLAB中不是每个矩阵都有逆矩阵的，比如一个矩阵的行列式是零的话，则矩阵的逆就不存在，这样的矩阵是奇异的。

MATLAB中，逆矩阵的计算使用 inv 函数：逆矩阵A是inv(A).

MATLAB特殊矩阵

MATLAB中的特殊阵列

MATLAB中会使用一些函数来建立一些特殊的矩阵，对于所有这些函数，一个参数创建一个正方形阵列，双参数创建矩形阵列。

使用 zeros(m,n) 函数建立一个元素为零的m*n的矩阵：

例如：

zeros(5)

MATLAB 执行上述语句，返回以下结果：

ans =
     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0
     0     0     0     0     0

使用 ones(m,n) 函数建立一个元素全为1的m*n矩阵：

例如：

ones(4,3)

MATLAB执行上述语句，返回以下结果：

ans =
     1     1     1
     1     1     1
     1     1     1
     1     1     1

使用 eye(m) 函数创建一个m维的单位矩阵：

例如：

eye(4)

MATLAB执行上述语句，返回以下结果：

ans =
     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1

使用 rand() 函数建立一个数组（0,1）上均匀分布的随机数：

例如：

rand(3, 5)

MATLAB执行上述语句，返回以下结果：

ans =
    0.8147    0.9134    0.2785    0.9649    0.9572
    0.9058    0.6324    0.5469    0.1576    0.4854
    0.1270    0.0975    0.9575    0.9706    0.8003

MATLAB幻方

产生相同的总和，当它的元素加入逐行，逐列或对角线幻方是一个正方形。

使用 magic() 函数创建一个幻方阵列，它需要一个单数的参数，该参数必须是一个大于或等于3的标量。

例如：

magic(4)

MATLAB执行上述语句，返回以下结果：

ans =
    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

MATLAB多维数组

在MATLAB中，一个阵列如果具有两个以上的维度则被称为多维数组。

在MATLAB中的多维数组是正常的两维矩阵的延伸。

MATLAB中需要先创建一个二维数组然后对该二维数组进行扩展，这样才能生成一个多维数组。

例如，我们先建立一个二维数组a。

a = [7 9 5; 6 1 9; 4 3 2]

MATLAB执行上述语句，返回以下结果：

a =
     7     9     5
     6     1     9
     4     3     2

数组 a 是一个 3x3 阵列，通过提供的值，我们可以添加一个第三维，例如：

a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]

MATLAB执行上述语句，返回以下结果：

a(:,:,1) =
     7     9     5
     6     1     9
     4     3     2

a(:,:,2) =
     1     2     3
     4     5     6
     7     8     9

同样，我们也可以使用 ones()， zeros() 或 rand() 函数建立多维数组。

例如：

b = rand(4,3,2)

MATLAB执行上述语句，返回以下结果：

b(:,:,1) =
    0.0344    0.7952    0.6463
    0.4387    0.1869    0.7094
    0.3816    0.4898    0.7547
    0.7655    0.4456    0.2760

b(:,:,2) =
    0.6797    0.4984    0.2238
    0.6551    0.9597    0.7513
    0.1626    0.3404    0.2551
    0.1190    0.5853    0.5060

还能够使用 cat() 函数来建立多维数组，它结合沿着指定的维度的数组列表：

cat() 函数的语法是：

B = cat(dim, A1, A2...)

注意：

B 是新建的数组；
A1, A2, ... 是要连接的阵列；
dim 是一起串联阵列的维度。

MATLAB冒号符号

MATLAB 中可以使用 “:” 来建立矢量、下标数组和指定的迭代，是最有用的 MATLAB 运算符之一。

可以使用冒号 “:” 运算符建立矢量指数来选择行、列或数组中的元素。

格式	目的
A(:,j)	是A的第 j 列
A(i,:)	是A的第 i 行
A(:,:)	是等效的二维数组；对于矩阵，这与 A 相同
A(j:k)	是A（j），A（j + 1），...，A（k）；矩阵A从第一列开始从上到下的第j个元素到第k个元素组成的行向量
A(:,j:k)	是 A(:,j)， A(:,j+1)，...，A(:,k)
A(:,:,k)	是三维数组 A 的第 k 页
A(i,j,k,:)	是四维数组 A 中的矢量；矢量包括 A（i，j，k，1），A（i，j，k，2），A（i，j，k，3）等
A(:)	是 A 的所有要素，被视为单列；在赋值语句的左侧，A（:) 填充A，保留以前的形状；在这种情况下，右侧必须包含与A相同数量的元素。

详细例子

a = [ 1 2 3 4; 5 6 7 8; 9 10 11 12;13 14 15 16];
a(1:4)

结果

ans =
     1     5     9    13

MATLAB函数

在MATLAB中，函数定义在单独的文件。函数和函数的文件名应该是相同的。

函数是一起执行任务的一组语句。

函数在自己的工作空间进行操作，被称为本地工作区，独立的工作区；在 MATLAB 命令提示符访问，这就是所谓的基础工作区的变量。

函数可以接受多个输入参数和可能返回多个输出参数。

函数语句的语法是：

function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

详细例子

下述有个 mymax 函数，它需要五个数字作为参数并返回最大的数字。

建立函数文件，命名为 mymax.m 并输入下面的代码：

function max = mymax(n1, n2, n3, n4, n5)
%This function calculates the maximum of the
% five numbers given as input
max =  n1;
if(n2 > max)
    max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
    max = n4;
end
if(n5 > max)
    max = n5;
end

每个函数的第一行要以 function 关键字开始。它给出了函数的名称和参数的顺序。

在我们的例子中，mymax 函数有5个输入参数和一个输出参数。

注释行语句的功能后提供的帮助文本。这些线条打印，当输入：

help mymax

MATLAB执行上述语句，返回以下结果：

This function calculates the maximum of the
 five numbers given as input

可以调用该函数：

mymax(34, 78, 89, 23, 11)

MATLAB执行上述语句，返回以下结果：

ans =
    89

MATLAB匿名函数

一个匿名的函数就像是在传统的编程语言，在一个单一的 MATLAB 语句定义一个内联函数。

它由一个单一的 MATLAB 表达式和任意数量的输入和输出参数。

在MATLAB命令行或在一个函数或脚本可以定义一个匿名函数。

这种方式，可以创建简单的函数，而不必为他们创建一个文件。

建立一个匿名函数表达式的语法如下：

f = @(arglist)expression

详细例子

在这个例子中，我们将编写一个匿名函数 power，这将需要两个数字作为输入并返回第二个数字到第一个数字次幂。

在MATLAB中建立一个脚本文件，并输入下述代码：

power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

运行该文件时，显示结果：

result1 =
   343
result2 =
     7
result3 =
   1.0000e-10
result4 =
    9.5459

MATLAB绘图

在MATLAB中绘制函数图形的步骤如下：

先定义变量 x，通过指定的变量 x 值的范围，该函数被绘制；
然后定义函数， y = f(x)；
最后调用 plot 命令，如 plot(x, y)。

让我们举一个例子，绘制函数 y = x²。

在这个例子中，我们将绘制两个图形具有相同的函数，但在第二次，我们将减少值的增量。

请注意，因为减少了增量，图形会变得平滑。

在MATLAB中建立一个脚本文件，输入下述代码：

x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)

MATLAB添加标题，标签，网格线和缩放的图形

我们可以在 MATLAB 中添加标题，调整 x 轴和 y 轴，网格线，并沿标签美化图形。

xlabel 和 ylabel 指令产生沿 x 轴和 y 轴的标签。
标题命令允许你生成图表上的一个标题。
网格命令允许你生成图上的网格线。
轴等于命令允许生成与同等规模因素和空间两个坐标轴上的积点。
轴方形命令生成一个正方形的积点。

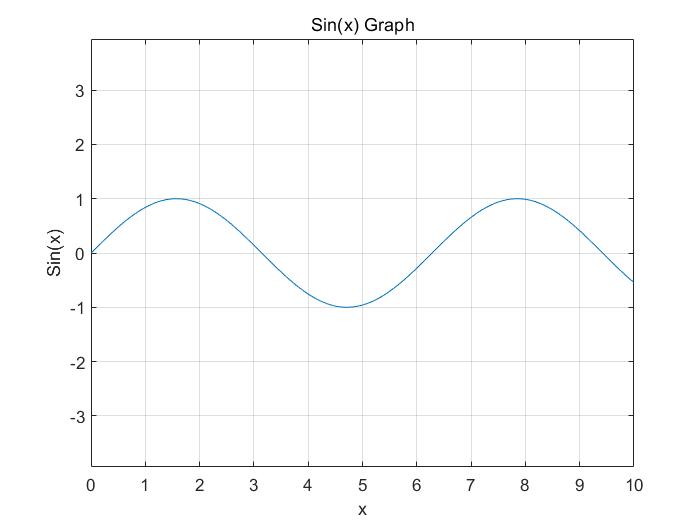
x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal

MATLAB在同一张图上绘制多个函数

在MATLAB中可以绘制多个图形相同的积点。

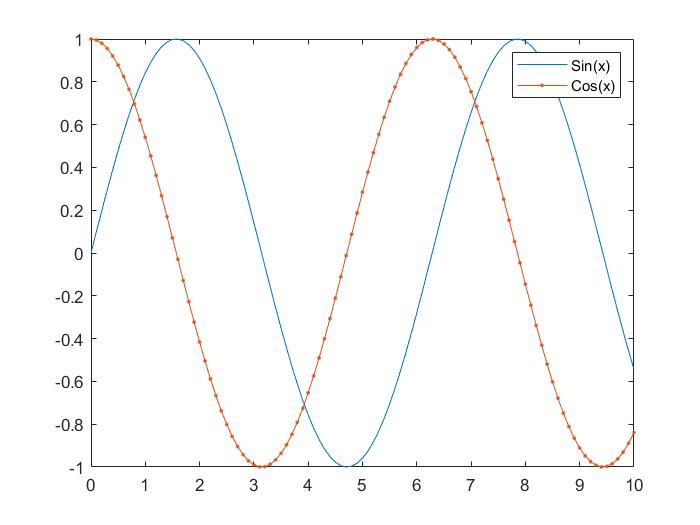
x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')

MATLAB在走势图上的颜色设置

MATLAB包含了八个绘制图形的基本颜色选项，下表提供了显示的颜色以及相应的代码：

Color	Code
White	w
Black	k
Blue	b
Red	r
Cyan	c
Green	g
Magenta	m
Yellow	y

具体示例

绘制两个多项式的图形：

f(x) = 3x⁴ + 2x³+ 7x² + 2x + 9 and
g(x) = 5x³ + 9x + 2

在MATLAB中建立一个脚本文件，并输入下述代码：

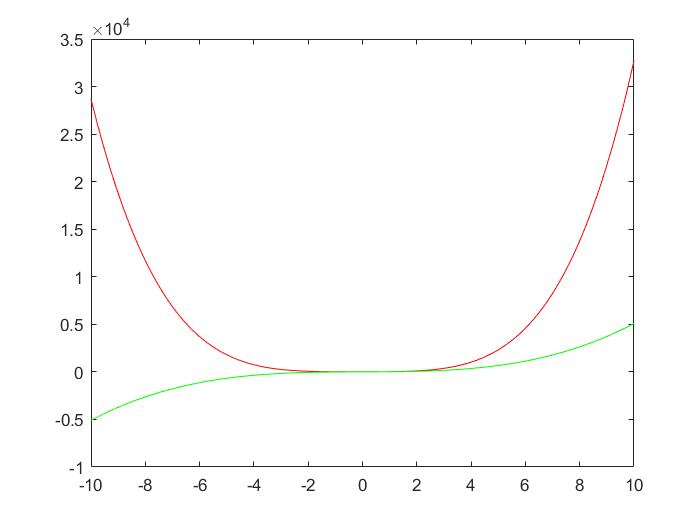
x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')

MATLAB设置轴刻度

该轴命令允许您设置轴的刻度，您可以提供的最小值和最大值的 x 和 y 轴，使用轴命令的方式如下：

axis ( [xmin xmax ymin ymax] )

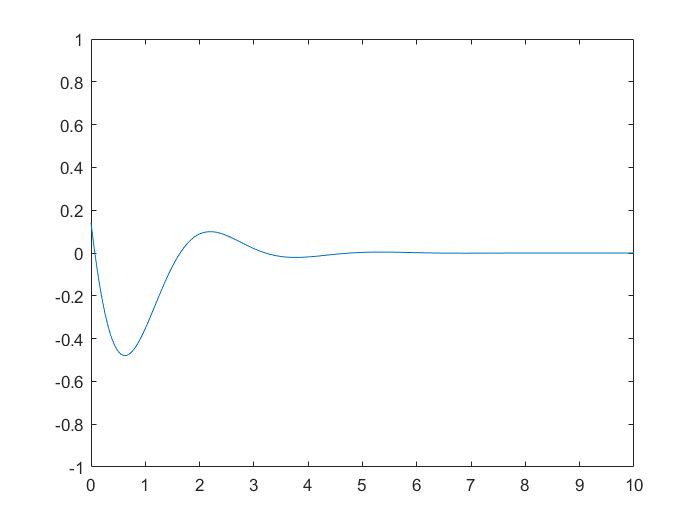
x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])

MATLAB生成子图

当创建一个数组地块在相同的数字，这些地块被称为子图。

MATLAB 中使用 subplot 命令创建子图。

subplot 命令的语法如下：

subplot(m, n, p)

其中，m 和 n 为积阵列的行和列的数量，p 指定把一个特定的积。

subplot 命令建立的每个绘图都可以有其自己的特点。

具体示例

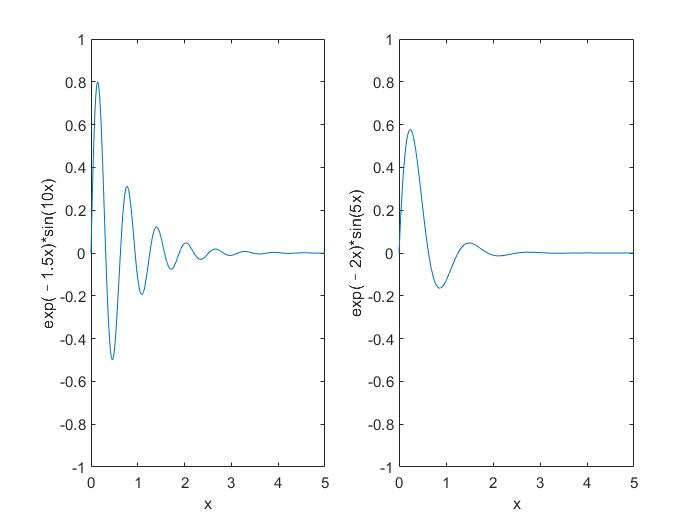
让我们生成下述的两个图：

y = e^−1.5xsin(10x)
y = e^−2xsin(5x)

x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(5*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(5x)'),axis([0 5 -1 1])

MATLAB图形

在上节内容中我们大概了解了MATLAB绘图的一些基本操作命令，在本节我们将继续探索MATLAB绘图和图形功能，内容包括：

如何绘制二维条形图
如何绘制等值线
如何绘制三维图

MATLAB绘制条形图

MATLAB 中使用 bar 命令绘制一个二维条形图。

具体示例

如果有一个包含10名学生的教室，这些学生获得的分数的百分比是75，58，90，87，50，85，92，75，60和95，使用这个数据，我们将绘制条形图。

在MATLAB中建立一个脚本文件，并输入下述代码：

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

运行该文件，MATLAB显示如下的棒形图：

MATLAB绘制三维图

三维图基本上显示的是由两个变量g = f(x，y)中的函数定义的表面。

像之前一样，要定义g，首先使用meshgrid命令在函数的域上创建一组(x，y)点。接下来，分配函数本身。最后，使用surf命令创建一个曲面图。

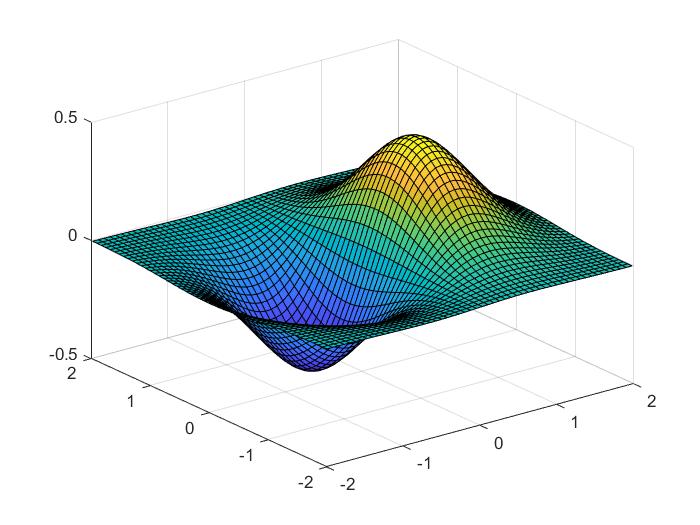
具体示例

为以下函数创建一个3D曲面图 g = xe^{-(x² + y²)}

在MATLAB中建立一个脚本文件，并输入下述代码：

[x,y] = meshgrid(-2:0.075:2);
z = x .* exp(-x.^2 - y.^2);
surf(x, y, z)
print -deps graph.eps

plot(1:64, device1_phase, 'b-', 'LineWidth', 2)

功能：绘制设备1的CSI相位随子载波变化的曲线。
参数细节：
- x轴：1:64 → 子载波编号（1到64）。
- y轴：device1_phase → 每个子载波的相位值（单位：弧度）。
- 线条样式：'b-' → 蓝色实线。
- 线条粗细：'LineWidth', 2 → 线宽2磅（比默认更粗，便于可视化）。

在MATLAB中，size(device1_csi, 1) 的作用是获取变量 device1_csi 的行数（即第一个维度的长度）。以下是详细解释：

1. `size(device1_csi, 1)` 的含义

device1_csi：这是一个二维矩阵（通常是 时间点 × 子载波 的CSI数据矩阵）。
size(device1_csi, dim)：
- dim=1 时：返回矩阵的行数（时间点的数量）。
- dim=2 时：返回矩阵的列数（子载波数量的两倍，因为包含实部和虚部）。
- 若省略 dim，则返回所有维度的长度（如 [行数, 列数]）。

posted on 2025-03-20 18:59 ᶜʸᵃⁿ 阅读(41) 评论(0) 收藏举报

刷新页面返回顶部

uacs2024

导航

公告

matlab基础语法

MATLAB格式命令

MATLAB创建向量

MATLAB switch语句语法

MATLAB while循环语法

MATLAB for 循环语法:

引用向量元素

MATLAB追加向量

MATLAB向量的模

MATLAB向量点积

详细例子

MATLAB矩阵

MATLAB引用一个矩阵的元素

将矩阵A中的第m行和第n行复制两次，创建一个新矩阵，则为：A([m,n,m,n],:)

MATLAB串联矩阵

详细例子

MATLAB矩阵的行列式

详细例子

MATLAB逆矩阵

MATLAB特殊矩阵

MATLAB中的特殊阵列

MATLAB幻方

MATLAB多维数组

MATLAB冒号符号

详细例子

MATLAB函数

详细例子

MATLAB匿名函数

详细例子

MATLAB绘图

MATLAB添加标题，标签，网格线和缩放的图形

MATLAB在同一张图上绘制多个函数

MATLAB在走势图上的颜色设置

具体示例

MATLAB设置轴刻度

MATLAB生成子图

具体示例

MATLAB图形

MATLAB绘制条形图

具体示例

MATLAB绘制三维图

具体示例

1. size(device1_csi, 1) 的含义

1. `size(device1_csi, 1)` 的含义