2021.09.07am

|---|预期|实际|
|A|100|80|
|B|100|80|
|C|100|100|
|D|100|100|
|E|100|100|
|F|10|0|
|G|0|100|
|H|100|100|
|S|610|560|

水菜

A 火车站 \(\blacktriangle\!\blacktriangledown\)

1. 这道题稍微推下式子便知道和斐波拉契数列有关
2. 但是我花了50分钟推出来个寂寞
3. 气急败坏选择放弃这个算法
4. 设第一站上车人数(初始)为 \(x\),第二站上车人数为 \(y\),定义两个用 \(x\) 和 \(y\) 表示的数组 \(sum\)表示此站后车上人数 ； \(add\) 表示本站上车人数
5. 那么很容易得到初始状态:

\[\begin{alignedat}{3} sum_x[1] & = 1 \\ sum_x[2] & = 1 \\ add_x[1] & = 1 \\ add_y[2] & = 1 \\ \end{alignedat} \]

以及转移方程：

\[\begin{alignedat}{3} & sum_x[i] & = sum_x[i-1]+add_x[i-2] \\ & sum_y[i] & = sum_y[i-1]+add_y[i-2] \\ & add_x[i] & = add_x[i-1]+add_x[i-2] \\ & add_y[i] & = add_y[i-1]+add_y[i-2] \\ \end{alignedat} \]

6. 注意：
   • 当解出来 \(y\) 不为非负整数时不成立。(\(y=0\)是成立的···\(10pts\))
   • 第 \(n\) 站是全部都下车，也就是说用的是 \(sum[n-1]\)

B 最大的子序列和 \(\blacktriangle\!\blacktriangledown\)

1. 一看数据:\(n \leq 10^7\) ，\(O(n \log n)\) 都不行，而且开数组就暴毙
2. 然后稍微思索一番，便能想到正解。
3. 区间长度没定，也就是说我们可以选择任意区间
4. 而一个区间\([i,j]\)的和可以表示为\(sum[j]-sum[i]\),那么在确定 \(j\) 的同时没我们找到最小的\(sum[i](sum[0]=0)\) 即可。
5. 也就是说，我们可以边输入便更新\(sum,minsum\)与\(ans=sum-minsum\)

C 合唱队列 \(\blacktriangle\!\blacktriangledown\)

1. 一开始整错了，以为可以排序，心想为啥是 \(4\)，然后一会才发现是求最长单调序列
2. \(ans=max(lenl[i]+lenr[i]-1),1\leq i \leq n\)

D 数字组合 \(\blacktriangle\!\blacktriangledown\)

1. 之前考过，就不多说了

E 乌龟棋 \(\blacktriangle\!\blacktriangledown\!\blacktriangle\)

王八棋

1. 前前后后大概花了我一个多小时，重构了三次。

2. 分为三个部分来说:怎么做？怎么存？怎么写？

   怎么做:

   • 对于很多的线性\(DP\) 来说，表示到哪停止比表示从哪开始要好表示得多。这主要得益于 \(DP\) 的无后效性与递推性
   • 这道题亦是如此。我想的便是到哪停止的最大分数。那么我们就只开个一维数组？
   • 很显然，这样不能完全表示出状态。到同一个位置，可能消耗不同类型不同数目的牌，而我们难以比较出哪种牌用的多哪种牌用得少效果更好 （不然就用贪心了）
   • 那么我们便设状态为：到哪停止，用了多少张1号牌，多少张2号牌，多少张3号牌，多少张4号牌，即 \(dp[p][i1][i2][i3][i4]\)

   怎么存:

   • 我们稍微计算便发现：存不下。我们需要\(350*41^4\)的空间，这显然\(MLE\)的。

   • 那我们稍微抠一点：既然一个位置 \(p\) 只能从 \(p-1,p-2,p-3,p-4\)转来，那么为了避免存到重复的位置，完全可以只开 \(dp[5][41][41][41][41]\)。

   • 但这样的空间也只是勉强而已，保险起见，最好还是继续优化。

   • 优化方式无非两种：滚动数组与避免重复表达。

   • 第一种已经用掉了，而第二种还可以同时优化时间复杂度。

   • 我们可以发现，使用一定数目的各类牌，只能到达同一个同一个地方

   • 换一句话说：只要确定三种牌的数目与位置，或只确定四种牌的数目，我们能推出所有描述状态所需的要素。

   • 那么我们可以将空间优化到\(41^4\)或\(5*41^3\)(这里还有一点，被优化掉的是1号牌，因为1号牌更好排序与剪枝）,而时间优化到\(41^4\)或\(350*41^3\)(前面一种是写题解时才想到，结果发现更好···；因为算法后面一种实际上并没有用)（接下来我们会使用第一种方法存储）

   怎么写：(经验教训)

   • 一开始我就老老实实写的递推。第一次选择的是优化掉4号牌，并且先枚举的1号牌，再2,3号牌根据瓶子里先放大石头再放小石头再放沙子最好倒水的道理，我们知道，这样不成功的可能性是很大的，时间复杂度不变但是常数很大，于是就选择了重构

   • 然后又是经典的递推。选择优化掉1号牌。但是样例一直是0，并且很难调试。这里贴上错误代码（来展示码量）

   inline void change(int p,int tip){
   int fr=(p-tip-1)%5+1;
   int frp=p-tip;
   int np=(p-1)%5+1;
   for(int i4=sum[4];i4>=zy[tip][4];i4--){
   	int he4=(sum[4]-i4)*4;
   	if(he4>frp)break;
   	for(int i3=sum[3];i3>=zy[tip][3];i3--){
   		int he3=(sum[3]-i3)*3+he4;
   		if(he3>frp)break;
   		for(int i2=sum[2];i2>=zy[tip][2];i2--){
   			int he2=(sum[2]-i2)*2+he3;
   			if(he2>frp)break;
   			if(frp-he2>sum[1]-zy[tip][1])continue;
   			zt[np][i2][i3][i4]=max(zt[np][i2][i3][i4],zt[fr][i2-zy[tip][2]][i3-zy[tip][3]][i4-zy[tip][4]]+in[p]);
   		}
   	}
   }	
   }
   

   • 最后选择用类记忆化搜索函数写，就要好调试很多

   inline int suan(int p,int i2,int i3,int i4){//这边用的是二类存储
   	if(p<=0)return 0;//实际上一类还要更方便
   	if(i2>sum[2])return 0;
   	if(i3>sum[3])return 0;
   	if(i4>sum[4])return 0;
   	if(i2*2+i3*3+i4*4+sum[1]<n-p)return 0;
   	if(zt[(p-1)%50+1][i2][i3][i4])return zt[(p-1)%50+1][i2][i3][i4];
   	return zt[(p-1)%50+1][i2][i3][i4]=max(max(max(suan(p-1,i2,i3,i4),suan(p-2,i2+1,i3,i4)),suan(p-3,i2,i3+1,i4)),suan(p-4,i2,i3,i4+1))+in[p];//每种卡片只有最多40个，开50的数组绰绰有余，避免重复
   }
   

F 低买\(\blacktriangle\!\blacktriangledown\!\blacktriangle\)

1. 骗分都没骗到

2. 考虑在最长下降子序列里套东西
   3.设以 \(i\) 结尾最长下降子序列长度为\(len[i]\)，种类数为 \(cnt[i]\)，第 \(i\) 个数的值为 \(a[i]\)

   一个规律：当\(len[i]=len[j] 且 a[i]=a[j](i < j)\) 时，则以 \(a[i]\) 结尾的所有最长下降子序列均与以 \(a[j]\) 结尾的重复

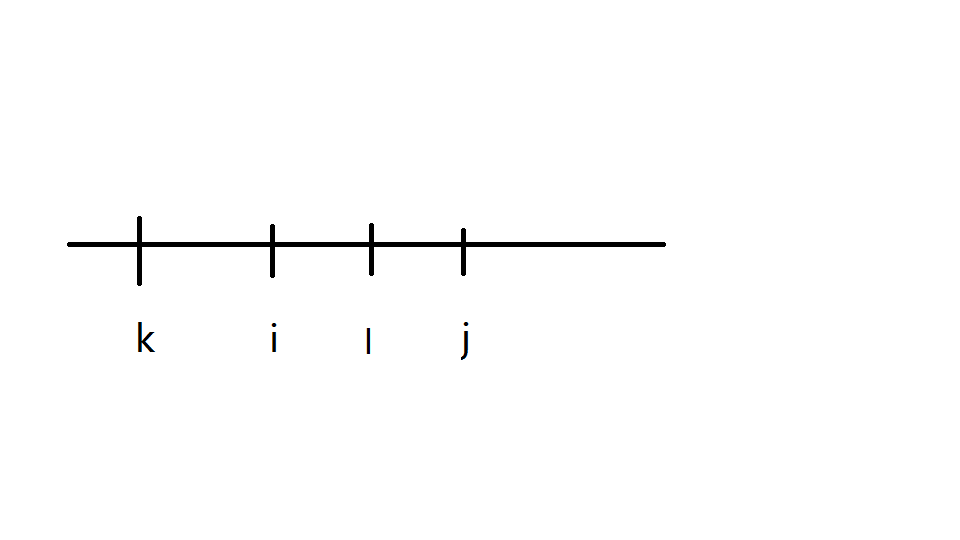
如图，\(\forall k,a[k]>a[i]且k<i\)
有 \(a[k]>a[j]且k<j\)
而，\(\forall l,a[l]>a[j]且l<j\)
一定不有 \(l<i\)
故，\(cnt[i] \leq cnt[j]\)恒成立
那么我们可以舍掉所有\(len[i]=len[j] 且 a[i]=a[j](i < j)\)的 \(i\),只保留 \(j\) ，便能保证不重复

G 炮兵阵地 \(\blacktriangle\!\blacktriangledown\!\blacktriangle\)

1. 状压 \(DP\) ，不是不可做题，但是没做
2. 符合题意就可(1代表放炮台，0代表不放)

\[ dp[i\!\mod 3][j][k]=\max(dp[(i-1)\!\mod 3][k][l]+va[j]) \]

3. 为了内存不爆，需要用滚动数组优化
4. 为了效率，最开始的可以像隔壁的大佬初始化找出可行的情况，也可以像我一样记忆化搜索。
5. 搜索子集可以像这样(复习一下):

	change=(1<<n)-1-used;
	for(int i=change;;i=(i-1)&change)

6. 实际时间复杂度应该是 \(O(m*8^n)\)，但是数据比较水，能过
7. 状压之前只做过一道，围棋，是道黑题，因为难度较高，就反而不利于掌握状压 \(DP\) 的套路写法，导致拿着题只能跳过。

H 数字三角形 \(\blacktriangle\)

emm，可以 \(DP\)(没必要) ，但我用的记忆化搜索

小总结

这次考试吧，代码重构了好多次。坏在还是习惯半懂就去写代码，好在能重构出来。

\(\cal {Made} \ {by} \ {YuGe}\)