浅谈spfa

算法简简简介

\(spfa\)，即\(Shortest \ Path \ Faster \ Algorithm\)，是\(Bellman-Ford\)的一个优化版本 （为什么Dijkstra优化了还是叫Dijkstra，你个spfa就可以改名啊！）...

算法讲解

回归正题，\(spfa\)主要是用一个\(dis\)数组来存储源点到每个节点的最短路，然后先将\(dis\)数组初始化为一个极大值，使得后面在松弛（其实就是求最短路啦）的时候能够被更新。我们把所有节点推到一个队列里面，然后每次取出队首进行松弛，如果说更新后的节点不在队列里面的话，就把它给推进队列里面，当队列为空时，最短路也就更新出来的QωQ。复杂度为 \(\Theta(KN)\) (\(k\)是一个常数，表示每个点进队的次数，随机图的话，\(k\)就在\(2\)左右。但是如果出题人毒瘤故意卡的话，\(k\)就会退化成边的条数)。

流程图：

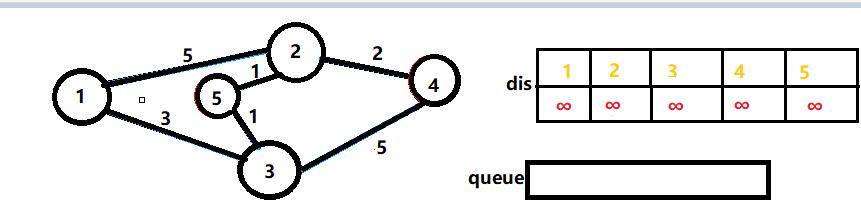
我们用这样一张无向图来作为例子。以节点1为起点，节点5为终点。

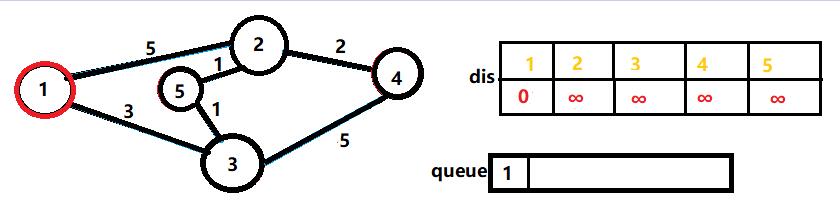
首先，我们将节点1推入队列之中，然后将dis[1]设为0。

其次，我们将1弹出队列，并将与其连着的2，3推入队列中，并将dis[2]更新为dis[1]+5=5，dis[3]更新为dis[1]+3=3。

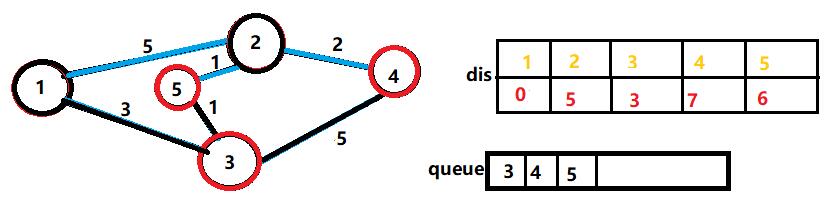
接着，我们将队首的2弹出，然后将dis[4]更新为dis[2]+2=7，将dis[5]更新为dis[2]+1=6，并将这两个点推入队列。

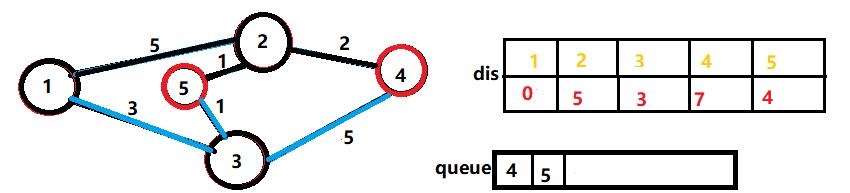
再接着，我们将队首的3弹出，然后发现dis[3]+5>dis[4]的，所以我们不能更新dis[4]，但是我们发现dis[5]可以更新，于是我们就把dis[5]更新为dis[3]+1=4。但是因为4处于队列中，我们就不再push进去。

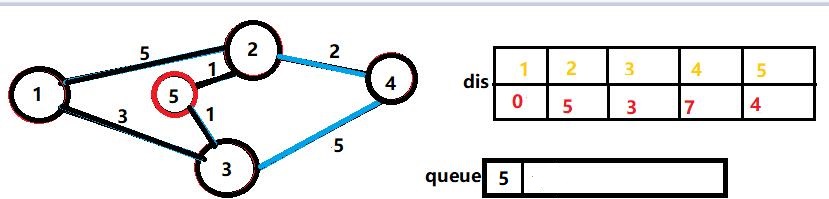
我们把队首的4弹出，发现什么也更新不了，于是啥也不做。

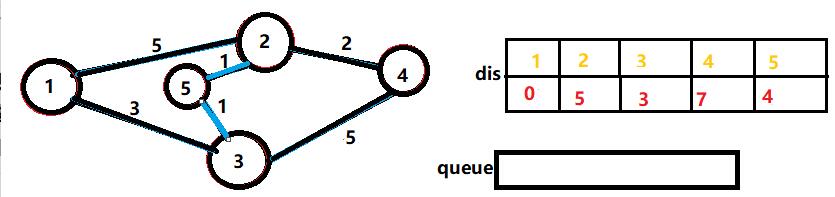
然后我们再次发现弹出5后也是啥也做不了……，于是最短路就求完啦！！！

空谈误国

来做一道spfa模板题吧！

\[ACcode \]

#include<bits/stdc++.h>
#define p_b push_back
#define m_p make_pair
//方便书写
using namespace std;
const int INF=2147483647,N=500005;
int n,m,st;//分别表示 点数 边数 起点
int u,v,w;//表示从点u->v的权值为w
vector<pair<int,int> > mp[N];//此处使用邻接表来存图，其实这个随意，看个人习惯
//因为还要存边权，所以用pair（struct也是可以的）
bool in[N];//判断一个点在不在队列中
int dis[N];//用来存储源点到所有点的最短距离
void spfa(int s) {//函数开始，传参传的是源点
    queue<int> q;//定义队列（你也可以手写）
    for(int i=1;i<=n;i++) dis[i]=INF;//将dis数组更新为极大值，既然本题中要求要2^31 -1，那么INF就特事特办
    memset(in,false,sizeof(in));//一定要初始化（除非你把数组定义在函数里面）
    q.push(st);//将源点推进队列中
    in[st]=true;//将源点标记为在队列中
    dis[st]=0;//源点到它自己的距离当然是0啦~
    while(!q.empty()){//只要队列非空
        int x=q.front();q.pop();//取出队首&弹出
        in[x]=false;//把弹出的元素标记为不在队列里面
        for(int i=0;i<mp[x].size();i++) {//遍历每一个跟x有边的节点
            int to=mp[x][i].first;//我们要更新的节点
            int w=mp[x][i].second;//边权
            if(dis[to]>dis[x]+w) {//如果说可以更新的话（我们要去的点离源点的长度比现在去这个点的长度达，我们就更新）
                dis[to]=dis[x]+w;//松弛
                if(!in[to]) {//如果说 更新后 的节点没有进队
                    q.push(to);//那么就把它推进去更新其他的点
                    in[to]=true;//把这个点标记为在队列中
                }
            }
        }
    }
}
int main() {
	scanf("%d%d%d",&n,&m,&st);
    for(int i=1;i<=m;i++) {
        scanf("%d%d%d",&u,&v,&w);
        mp[u].p_b(m_p(v,w));
        //mp[v].p_b(m_p(u,w))去掉注释就是双向边（无向边）
    }
    spfa(st);
    for(int i=1;i<=n;i++) printf("%d ",dis[i]);
	return 0;
}

关于\(spfa\)の梗

\(spfa\)一直是受人欢迎的最短路算法，直到那个\(NOI \ 2018\)黑暗的\(Day1\):

于是网上便广大流传："我\(spfa\)了"之类的话，所以说笔者在此处劝诫大家：在不是判负环或者单纯最短路的时候，千万不要用\(spfa\)，因为你永远也不会知道你遇见的出题人有没有那么毒瘤爱卡算法。（老老实实写\(Dijkstra\)吧！）