卡特兰数

卡特兰数可解决如下问题：
出栈次序。一个栈的进栈序列为1,2,3,4,5...,n，有多少种出栈序列。
n对括号有多少种匹配方式。
n个矩阵连乘，由于结合律，有多少种括号化的计算方案。
n个结点构成二叉树有多少种构造方案。
圆上有2n个点，两两连成线段，且线段互不相交，有多少种方案。
一个凸多边形划分为三角形区域有多少种方案。
从原点出发，每次向x或y轴正方向移动1单位，到达点(n,n)，且在移动过程中不越过第一象限平分线的移动方案数。

这种问题都有一个类似的做法，就是取一种方案把问题分成两个子问题
最后一个出栈的元素把问题分为小于这个元素出栈入栈的方法数和大于这个元素出栈入栈的方法数。
括号匹配是把问题分为在一对括号里面和在一对括号外面
矩阵连乘左边右边
二叉树左子树右子树
圆上2n个点也是类似括号匹配
凸多边形也是一条线划分左右两部分

然而这些方法数都怎么求，是有一个递推公式
h(n)=h(0)h(n-1)+h(1)h(n-2)+...+h(n-1)*h(0)
初始化某些值就可以求了

卡特兰数和组合数也有关系，最后的走格子问题就把这两个问题结合在了一起。

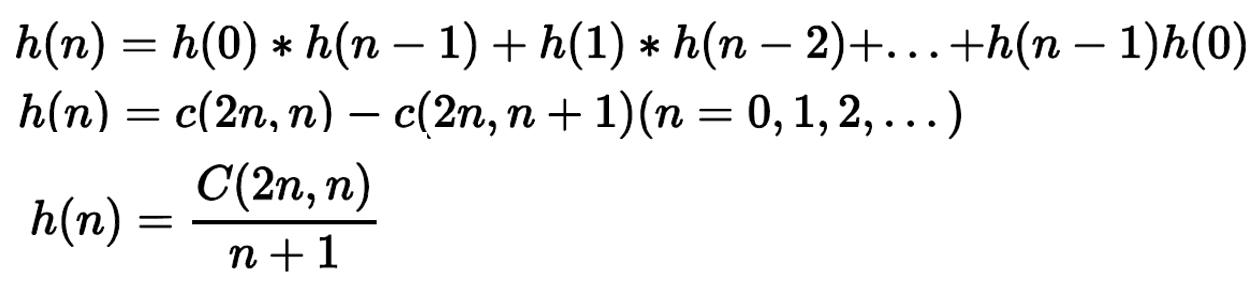
下面是递推公式的实现

#include<iostream>
#include<stdio.h>
using namespace std;

const int maxn = 20;
int n;
long long h[maxn];

int main()
{
    cin >> n;
    h[0] = 1, h[1] = 1;
    for (int i = 2; i <= n; i++) {
        for (int j = 0; j < i; j++) {
            h[i] += h[j] * h[i - j - 1];
        }
    }
    cout << h[n] << endl;

}