动态规划案例

动态规划一般有三步，定义子问题，这个子问题有着最优子结构，如果选取不合适可能无法解题；分析最优解的特点找到当前问题的最优解与最优子结构的关系，利用已经解决的子问题解决更大的问题，通常是最难的；初始化，极端情况的赋值，一般比较简单。

1、二项式系数计算问题
二项式系数用阶乘计算，也可采用杨辉三角加法解决，可算是一个线性规划问题。

2、DAG（有向无环图）最长路径问题

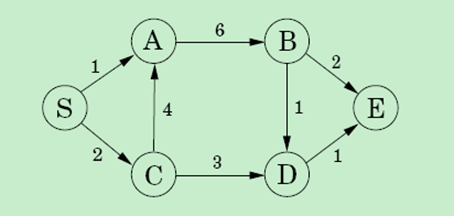
将图变化一下：

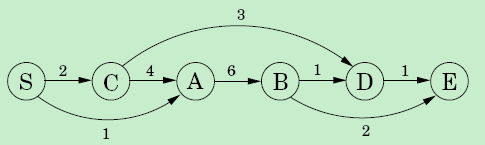
最长路径的起点是入度为0的点，终点是出度为0的点，u是v的前继，每一个结点都计算起点到这个点的最长距离，而这个点的最长距离是依赖和它直接相连的前继结点+两点之间距离去max得来的，也就完成了longest path。

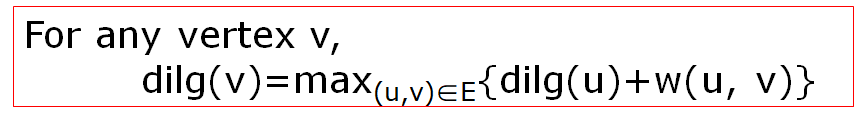
3、编辑距离

关注两个字符串的最后一列分类讨论，如果一对一比较是否相同，如果一对空直接加1

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>

#include<string.h>

char str1[100], str2[100];
int E[100][100];

int MIN_Three(int a, int b, int c)
{
	if (a <= b) {
		if (a <= c)return a;
		else return c;
	}
	else {
		if (b <= c)return b;
		else return c;
	}
}

int main()
{
	scanf("%s %s", str1, str2);
	int len1 = strlen(str1);
	int len2 = strlen(str2);
	for (int i = 0; i <= len1; i++)E[0][i] = i;
	for (int i = 0; i <= len2; i++)E[i][0] = i;
	for (int i = 1; i <= len1; i++)
	{
		for (int j = 1; j <= len2; j++)
		{
			if (str1[i] == str2[j]) {
				E[i][j] = MIN_Three(E[i - 1][j] + 1, E[i][j - 1] + 1, E[i - 1][j - 1]);
			}
			else E[i][j] = MIN_Three(E[i - 1][j] + 1, E[i][j - 1] + 1, E[i - 1][j - 1] + 1);
		}
	}
		

	printf("%d\n", E[len1][len2]);
}

4、背包问题（每个物品可选无数次）

#include<iostream>
#include<algorithm>

using namespace std;

int weight[105], value[105];//最多输入100个物品
int W;//背包所能承受的最大重量
int n;//有多少物品可供选择

int K[10005];//背包承受的重量不能超过10000

int main()
{

	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i];

	for (int i = 1; i <= W; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			if (i >= weight[j])K[i] = max(K[i], K[i - weight[j]] + value[j]);
		}
	}
	cout << K[W];

}

5、背包问题（每个物品最多选一次）

#include<iostream>
#include<algorithm>

using namespace std;

int weight[105], value[105];//最多输入100个物品
int W;//背包所能承受的最大重量
int n;//有多少物品可供选择

int K[1005][105];//背包承受的重量不能超过1000

int main()
{

	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> weight[i] >> value[i];
	for (int i = 1; i <= n; i++)K[0][i] = 0;
	for (int i = 1; i <= W; i++)K[i][0] = 0;
	for (int i = 1; i <= W; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			if (i >= weight[j])K[i][j] = max(K[i][j - 1], K[i - weight[j]][j - 1] + value[j]);
			else K[i][j] = K[i][j - 1];
		}
	}
	cout << K[W][n];

}

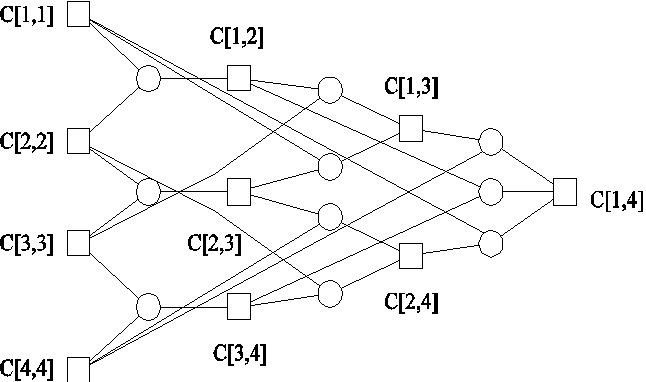
6、矩阵连乘
n个矩阵相乘，因为结合律，矩阵计算的先后顺序不同，结合的先后计算的次数也不同，求出最小的计算次数

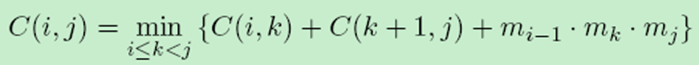
#include<iostream>
  #include<algorithm>
#include<limits.h>
using namespace std;

typedef struct Matrix
{
	int line_number;
	int column_number;
};

  Matrix M[105];//最多输入100个矩阵

int Q[105][105];//从i到j矩阵乘积的最小花销
int n;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> M[i].line_number >> M[i].column_number;

for (int i = 1; i <= n; i++)
	for (int j = 1; j <= n; j++)
		if (i == j)Q[i][i] = 0;
		else Q[i][j] =INT_MAX;
	
for (int s = 1; s < n; s++) {
	for (int i = 1; i <= n-s; i++) {
		int j = i + s;
		for (int k = i; k <j; k++)
			Q[i][j] = min(Q[i][j], Q[i][k] + Q[k + 1][j] + M[i].line_number * M[k + 1].line_number * M[j].column_number);
	}
}
cout << Q[1][n];

}