树状数组

树状数组是一种特殊的结构，并不是完全的树，而是与一个数组长度相等的另一个数组
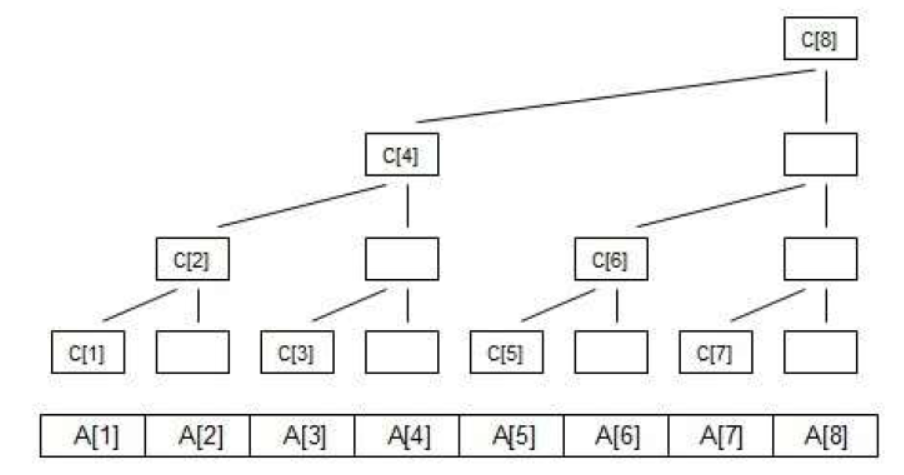
设原数组为A[]，树状数组为C[]
C数组里的元素是A数组若干个元素之和，而求和是有一定规律
用树状数组求和是logN的效率

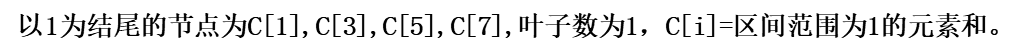
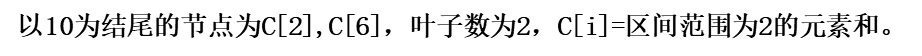
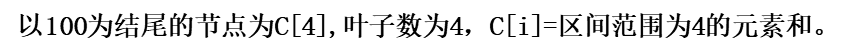
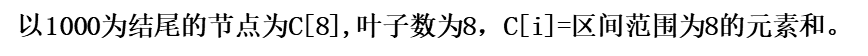
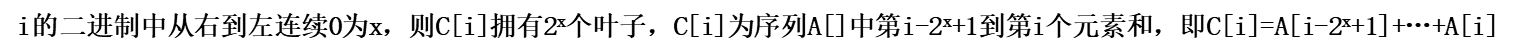
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;

const int N = 1000;
int A[N], C[N];
int n;
/*
lowbit函数 给一个整数i
计算出i的二进制数末尾有x个连续的0
2^x=i and -i
证明：
i=A1B(B=00...0)
-i=A'0b'(b'=11...1)+1=A'1B
i and -i=00...01B=2^x
*/

int Sum(int num)//求前num个元素之和
{
	int s=0;
	while (num > 0) {
		s += C[num];
		num = num - (num & (-num));
	}
	return s;
}

void Change(int add,int i)//第i个元素增加了add
{
	while (i <= n) {
		C[i] += add;
		i = i + (i & (-i));
	}
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> A[i];
	for (int i = 1; i <= n; i++) {
		for (int j = i - (i & (-i)) + 1; j <= i; j++)
			C[i] += A[j];
	}
	int s = Sum(7);//求前7个数的和
	int S = Sum(7) - Sum(3);//求第4到第7的和
	A[3] += 1;
	Change(1, 3);
	for (int i = 1; i <= n; i++)cout << C[i] << endl;
}