Data-Structure01-绪论

---恢复内容开始---

 

一.作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3
   实验要求：
9. 抽象数据类型名为Rational。
10. 有理数分母不能为负数或者0，类似输入请提示重输入。
11. 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成，实现用CPP文件完成。Main.cpp文件实现数据输入输出。
12. 数据输入输出格式参考如下：
    输入：
    1 3 //T1的分子、分母
    1 2 //T2的分子、分母
    ** 输出：**
        5 6  //两个有理数相加
        -1 6  //两个有理数相减
         1 6  //两个有理数相乘
         2 3  //两个有理数相除
13. 程序应对异常输入或者出错必要处理和提示，比如提示：“分数是否需要约分等”。                                                                                                                                                                                                                                      

    二.作业内容                                                                                                                                                                                                                                                                        1. 用ADT的抽象数据模型描述你的有理数数据类型                                                                                                                                                                                               

    ADT Rational {
    数据对象：D={<e1,e2> | e1,e2∈整数}
    数据关系：R={ <e1,e2> ，e1是有理数的分子，e2是有理数的分母，且e2≠0}
    基本操作：
    InitRational(&T,v1,v2)
    DestroyRational(&T)
    GetRational(T,i,&e)
    PutRational(T,i,e)
    AddRational(T1,T2,&T3)
    SubRational(T1,T2,&T3)
    MulRational(T1,T2,&T3)
    DivRational(T1,T2,&T3)
    } ADT Rational

         2.头文件                                                                                                                                                                                                                                                                                                                                                                                                                                                                                3.函数说明                                                                                                                                                                                                                                                                                  

    主函数

           

    int main()
    {
    int R1[2],R2[2],R3[2];
    int e,e1,e2;
    int i;
    int *R=NULL;
    create(R,4,3);
    
    back(R,e,1);
    
    change(R,e,2);
    
    destory(R);
    
    cout<<"输入两个数分别代表R1分子和分母，中间以空格分隔"<<endl; //在主函数中录入数值
    do{
    cin>>e1;
    cin>>e2;
    if(e2<=0)
    cout<<"分母不能为负数或者零,请重新输入"<<endl;
    else
    break;
    }while(1);
    R1[0]=e1;
    R1[1]=e2;
    reduction(R1[0],R1[1]);
    
    cout<<"输入两个数分别代表R2分子和分母，中间以空格分隔"<<endl;
    do{
    cin>>e1;
    cin>>e2;
    if(e2<=0)
    cout<<"分母不能为负数或者零,请重新输入"<<endl;
    else
    break;
    }while(1);
    R2[0]=e1;
    R2[1]=e2;
    reduction(R1[0],R1[1]);
    
    add(R1[0],R1[1],R2[0],R2[1]);
    
    subtract(R1[0],R1[1],R2[0],R2[1]);
    
    multiply(R1[0],R1[1],R2[0],R2[1]);
    
    division(R1[0],R1[1],R2[0],R2[1]);
    
    return 0;
    }

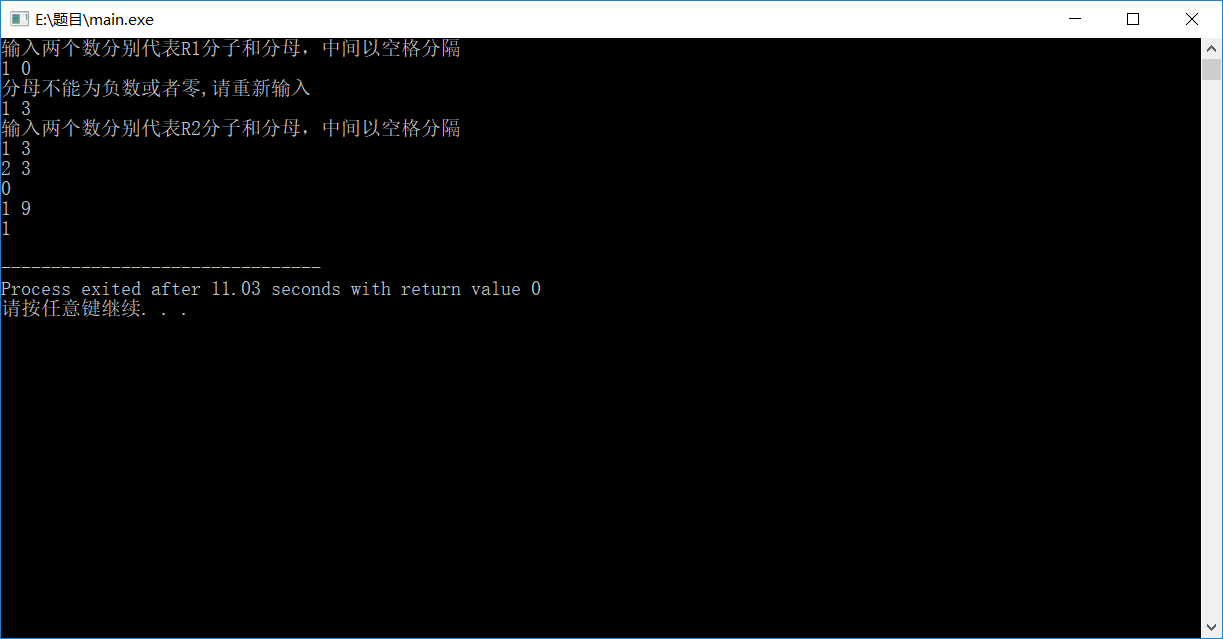
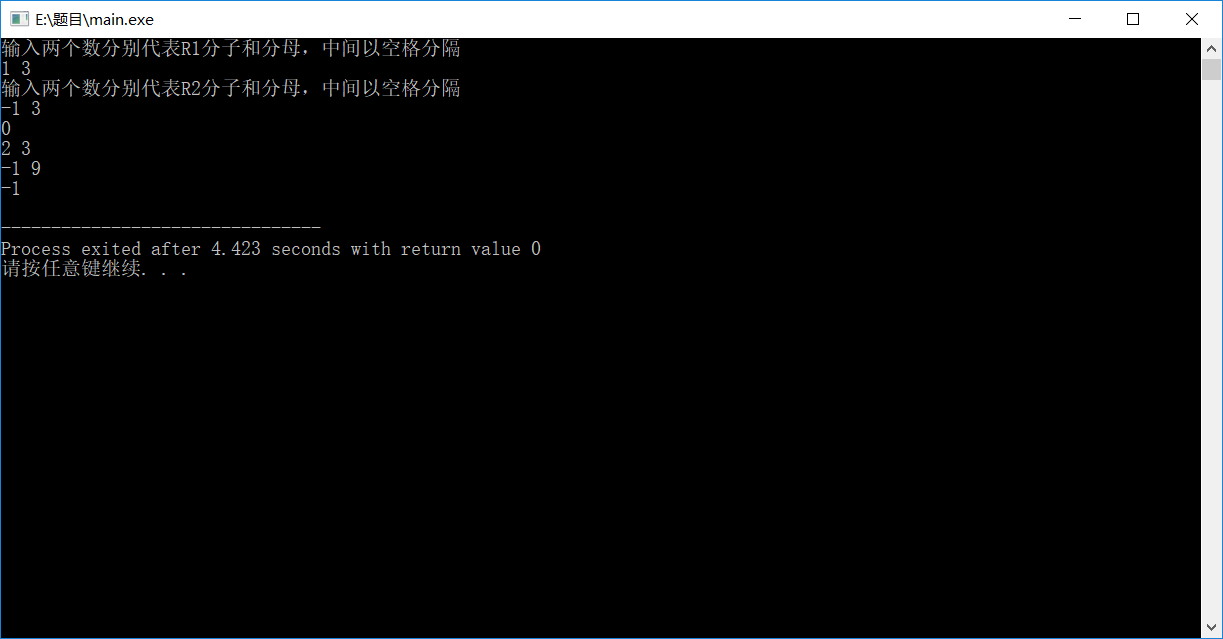
    三.运行结果                                                                                                                  

                                                                                                                                                                                                                                                                                                                                     当分母为零时                                                                             

                                                                                                                                                                                                   四.总结                                                                                                                                                                                                                                                                           

                            在分数中要注意分子和分母的约分问题

　　                    整数问题也要考虑结果是否存在负数，或是分子分母同时为负时的情况