splay 小记
众所周知,tzc 一般写平衡树都用 fhq-treap,但是由于本人过于 sb,学过的东西都忘掉了,所以在复习 LCT 前特地前来复习一下 splay 了(/cg/cg/cg
前言
我们知道,一个有序序列 \(a\) 的二叉搜索树是一棵特殊的带上权值的二叉树,满足其中序遍历就是序列 \(a\)。显然一个序列 \(a\) 的二叉搜索树并不唯一,并且如果我们暴力将这些值一一插入二叉搜索树复杂度最坏可以达到 \(\mathcal O(n^2)\),反例 \(n,n-1,n-2,\cdots,1\),因此我们需要使用一些奇淫技巧将二叉树的复杂度降到 \(\mathcal O(\log n)\)。
splay 的基本思想
众所周知 fhq-treap 和 treap 使用的是随机权值保证复杂度,fhq-treap 则还使用了分裂、合并操作支持区间操作,可这次咱们偏不使用随机权值的方式保证复杂度,咱们使用更加玄学的技巧——伸展操作保证复杂度。具体来说,splay 伸展保证复杂度是基于这样一个思想:每次将查询一个节点就把它搬到根,这样查找频率较高的点就能离根节点较近,进行若干次这样的操作之后树的高度就摊到期望 \(\log n\) 级别了。
这个梦想非常美好,但是要实现这个梦想我们还要支持一些操作,譬如如何实现将一个点搬到根这样的操作。
旋转操作
显然我们如果想要将一个点转到根,首先要学会怎样将一个点转到他父亲的位置,这也正是旋转操作的核心所在,根据上文可知,对于一个有序序列,它的二叉搜索树的形态是不唯一的,因此对于一个 \(5\) 个节点的二叉搜索树(如下图),我们可以通过旋转操作将它由左图变为右图,并且中序遍历不发生变化。
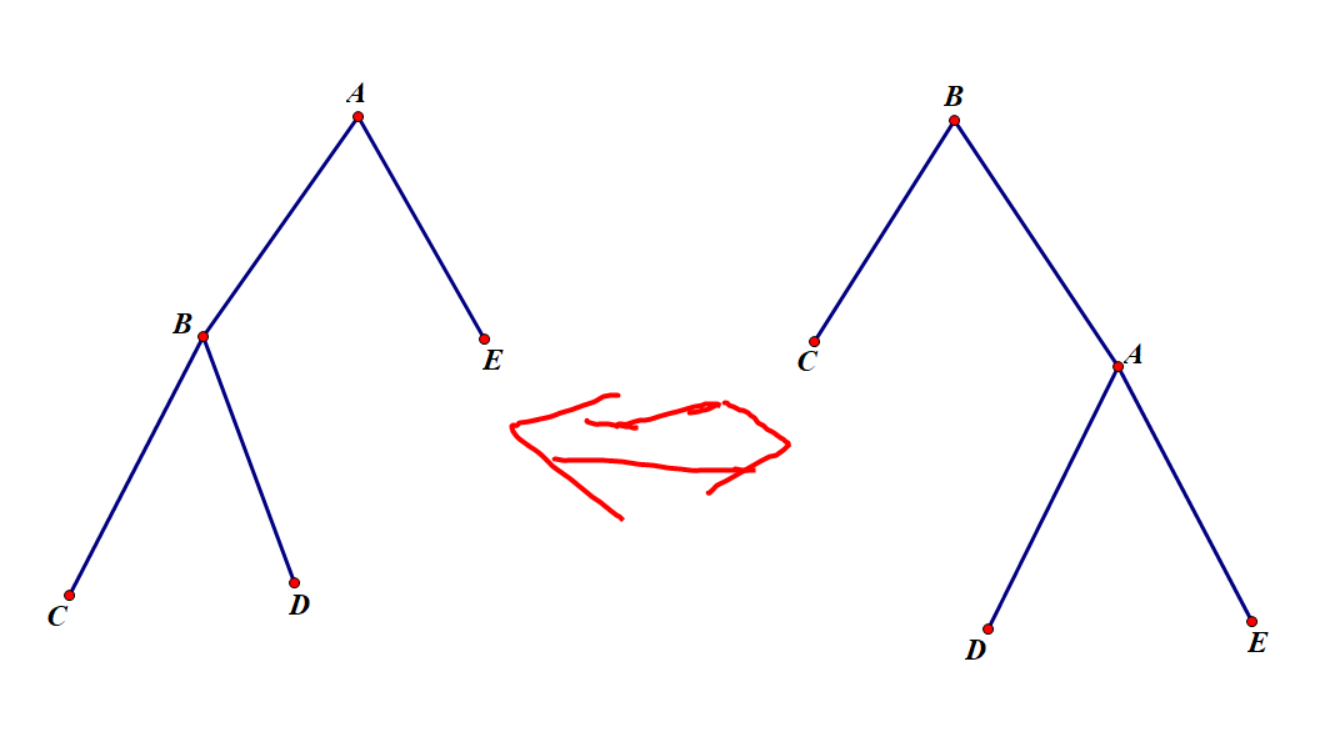
上图中,由左图变为右图的过程中,\(A\) 右子树的大小小于 \(B\) 右子树的大小,因此整个伸展树的重心右移,因此被称为右旋(zig),反过来的操作也就被称为左旋(zag)。
用文字语言来描述右旋的操作,就是:
- 对于伸展树上的一个点 \(B\),我们假设它的父亲为点 \(A\),那么 \(B\) 能通过右旋操作移到点 \(A\) 的位置当且仅当 \(B\) 是 \(A\) 的左儿子。
- \(B\) 的右儿子为点 \(D\),那么有右旋之后:
- \(B\) 的左儿子与 \(A\) 的右儿子都没有发生变化
- \(B\) 的右儿子变为 \(A\)
- \(A\) 的左儿子变为 \(B\) 原来的右儿子即点 \(D\)
显然对于任意一棵伸展树上对任意一个不是根节点的点 \(X\) 进行旋转操作都可以将它简化为上图中五个节点的树的旋转操作,因为记 \(X\) 的父亲为 \(Y\),那么显然旋转操作与 \(Y\) 子树以外的节点没有任何关系,因此我们可以直接忽略 \(Y\) 子树外的节点,而如果我们把 \(X\) 左右子树、\(Y\) 的右子树分别缩成一个点,就会得到上面的图。
旋转操作的基本思想这么多,下面就到了考验我们代码能力的时候了。如何清晰明了而又不用大量分类讨论地实现旋转操作呢?
我们首先定义 \(\text{ident}(x)\) 表示 \(x\) 是其父亲的左儿子还是右儿子,代码如下:
int ident(int k){return (s[s[k].f].ch[0]==k)?0:1;}
那么显然定义了这个函数之后我们就 duck 不必将左旋右旋分开来实现了,可以直接根据 \(x\) 是其父亲的左儿子/右儿子来判断到底应进行左旋还是右旋,同时我们再定义函数 \(\text{connect}(x,f,op)\) 表示将 \(x\) 设为 \(f\) 的 \(op\) 儿子,其中 \(op=0\) 表示左儿子,\(op=1\) 表示右儿子,那么显然 \(\text{connect}(x,f,op)\) 可以这样实现:
void connect(int k,int f,int op){s[k].f=f;return ((!f)?(rt=k):(s[f].ch[op]=k)),void();}
接下来考虑怎样使用 \(\text{connect}\) 和 \(\text{ident}\) 函数实现旋转操作,我们设 \(X\) 的父亲为 \(Y\),\(Y\) 的父亲为 \(Z\),\(dx=\text{ident}(x),dy=\text{ident}(y)\),那么旋转操作用以下三个语句即可实现:
- \(\text{connect}(ch[x][dx\oplus 1],y,dx)\)
- \(\text{connect}(y,x,dx)\)
- \(\text{connect}(x,z,dy)\)
以左旋为例,执行这三个操作后得到的图如下图所示:
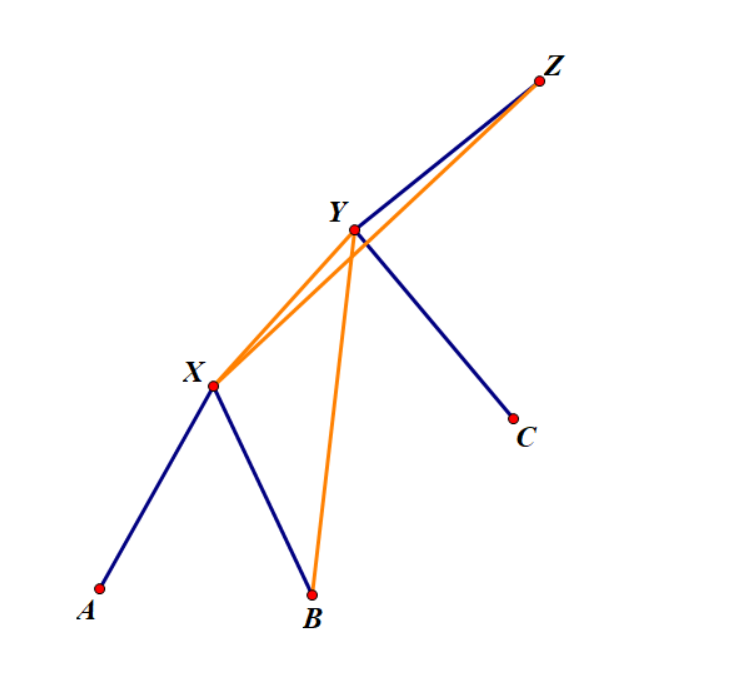
这样即可实现 \(\text{rotate}\) 函数,别忘了每次一个节点的儿子发生改变时都要 pushup!!111
void rotate(int x){
int y=s[x].f,z=s[y].f,dx=ident(x),dy=ident(y);
connect(s[x].ch[dx^1],y,dx);connect(y,x,dx^1);connect(x,z,dy);
return pushup(y),pushup(x),void();
}
伸展操作
通过上文我们已经懂得了如何将一个节点旋到它父亲所在的位置,那么如何将一个点旋转到根呢?
一个很显然的想法是不断上旋直到 \(x\) 的父亲位置,但是很抱歉这样复杂度是错误的,一条长度为 \(100000\) 的链,每次间隔查询 \(1,100000\) 就能把上述做法叉到平方。
那么有什么优化方法呢?其实在上述操作中加一点点小小的优化即可将复杂度降到严格单 \(\log\):
- 如果 \(x\) 的父亲就是根节点,那么直接一边上旋即可
- 否则如果 \(\text{ident}(x\text{的父亲})=\text{ident}(x)\),那么先旋转 \(x\) 的父亲后旋转 \(x\)
- 否则旋转两遍 \(x\)。
可以证明双旋的复杂度是严格 \(n\log n\) 的,较为感性的证明是将一个点 \(x\) 双旋至根会使其到根路径上每个点的深度减半,其余点的深度至多 \(+2\),较为理性的证明可以戳这里,由于此人数学比较菜没有看懂就不在这里重复了。
这一部分的代码如下:
void splay(int k,int to=0){
while(s[k].f!=to){
if(s[s[k].f].f==to) rotate(k);
else if(ident(k)!=ident(s[k].f)) rotate(k),rotate(k);
else rotate(s[k].f),rotate(k);
}
}
其他操作
懂得了 rotate 和 splay 这两个基本操作之后我们就可以用它来搞点事情(bushi,大雾)了
插入一个点:就不断递归加入到对应点的对应位置然后将它转到根即可。
删除一个点:将待删除点转到根,如果根节点没有左儿子就直接将根节点设为根节点的右儿子即可,否则记 \(u\) 为根节点左子树中权值最大的节点,将 \(u\) 转到根节点左儿子的位置,然后依次执行将 \(u\) 点的右子树设为根节点的右儿子、将 \(u\) 点设为根节点,删除原根节点即可,正确性显然。
查排名、前驱后继:都和 fhq-treap 没有区别,只不过最好用非递归的方式实现,因为最后要将查到的点转到根,如果使用递归查询则无法较为简单地处理“转到根”这一操作。
u1s1 其实这些操作熟悉与不熟悉没有区别,反正学 splay 只是因为 LCT 要用到 splay,平时平衡树谁有心思写个码量大+调试难度大的 splay 啊,不是自讨苦吃吗/cy/cy
模板题代码(调了 4h,精神直接崩溃/ll):
const int MAXN=1.1e6;
const int INF=0x3f3f3f3f;
struct node{int ch[2],val,f,siz,cnt;} s[MAXN+5];
int ncnt=0,rt=0;
void pushup(int k){s[k].siz=s[s[k].ch[0]].siz+s[s[k].ch[1]].siz+s[k].cnt;}
int newnode(int v,int f){s[++ncnt].val=v;s[ncnt].f=f;s[ncnt].siz=s[ncnt].cnt=1;return ncnt;}
int ident(int k){return (s[s[k].f].ch[0]==k)?0:1;}
void connect(int k,int f,int op){s[k].f=f;return ((!f)?(rt=k):(s[f].ch[op]=k)),void();}
void rotate(int x){
int y=s[x].f,z=s[y].f,dx=ident(x),dy=ident(y);
connect(s[x].ch[dx^1],y,dx);connect(y,x,dx^1);connect(x,z,dy);
return pushup(y),pushup(x),void();
}
void splay(int k,int to=0){
while(s[k].f!=to){
if(s[s[k].f].f==to) rotate(k);
else if(ident(k)!=ident(s[k].f)) rotate(k),rotate(k);
else rotate(s[k].f),rotate(k);
}
}
int ins(int v){
if(!rt) return rt=newnode(v,0);
int k=rt;while(k){
s[k].siz++;
if(s[k].val==v) return s[k].cnt++,k;
else if(v<s[k].val){
if(!s[k].ch[0]) return s[k].ch[0]=newnode(v,k);
else k=s[k].ch[0];
} else {
if(!s[k].ch[1]) return s[k].ch[1]=newnode(v,k);
else k=s[k].ch[1];
}
} assert(114514^1919810^114514^1919810);
}
void insert(int v){int x=ins(v);splay(x);}
int find(int k,int v){
if(!k) return -1;
if(s[k].val==v) return k;
else if(v<s[k].val) return find(s[k].ch[0],v);
else return find(s[k].ch[1],v);
}
void del(int v){
int x=find(rt,v);assert(~x);splay(x);
if(s[x].cnt>1) return s[x].cnt--,s[x].siz--,void();
if(!s[x].ch[0]) rt=s[x].ch[1],s[rt].f=0;
else{
int y=s[x].ch[0];assert(y);while(y&&s[y].ch[1]) y=s[y].ch[1];
splay(y,x);connect(s[x].ch[1],y,1);connect(y,0,1);pushup(y);
} s[x].ch[0]=s[x].ch[1]=s[x].cnt=s[x].siz=s[x].val=s[x].f=0;
}
int getrnk(int v){
int cur=rt,tot=0;
if(!rt) return 1;//fuck you! my 4 hours! my 4 hours! my whole morning!!!!!!1111
while(cur){
if(v<=s[cur].val){
if(!s[cur].ch[0]){tot++;break;}
else cur=s[cur].ch[0];
} else {
tot+=s[s[cur].ch[0]].siz+s[cur].cnt;
if(!s[cur].ch[1]){tot++;break;}
else cur=s[cur].ch[1];
}
} splay(cur);return tot;
}
int getxth(int x){
int cur=rt;
while(cur){
if(x<=s[s[cur].ch[0]].siz) cur=s[cur].ch[0];
else if(x>s[s[cur].ch[0]].siz+s[cur].cnt)
x-=s[s[cur].ch[0]].siz+s[cur].cnt,cur=s[cur].ch[1];
else break;
} splay(cur);return s[cur].val;
}
int getpre(int v){
int nd=0,cur=rt;
while(cur){
if(v<=s[cur].val) cur=s[cur].ch[0];
else nd=cur,cur=s[cur].ch[1];
} return assert(nd),splay(nd),s[nd].val;
}
int getnxt(int v){
int nd=0,cur=rt;
while(cur){
if(v>=s[cur].val) cur=s[cur].ch[1];
else nd=cur,cur=s[cur].ch[0];
} return assert(nd),splay(nd),s[nd].val;
}
int n,m;
int main(){
// freopen("C:\\Users\\汤\\Downloads\\P6136_6.in","r",stdin);
scanf("%d%d",&n,&m);int pre=0,ans=0;s[0].val=-1;
for(int i=1,x;i<=n;i++) scanf("%d",&x),insert(x);
while(m--){
int opt,x;scanf("%d%d",&opt,&x);x^=pre;
// if(m%1000==0) printf("%d\n",x);
if(opt==1) insert(x);
else if(opt==2) del(x);
else if(opt==3) ans^=(pre=getrnk(x));
else if(opt==4) ans^=(pre=getxth(x));
else if(opt==5) ans^=(pre=getpre(x));
else if(opt==6) ans^=(pre=getnxt(x));
} printf("%d\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号