LOJ 3066 - 「ROI 2016 Day2」快递(线段树合并+set 启发式合并)
人傻常数大,需要狠命卡……/wq/wq
画个图可以发现两条路径相交无非以下两种情况(其中红色部分为两路径的重叠部分,粉色、绿色的部分分别表示两条路径):
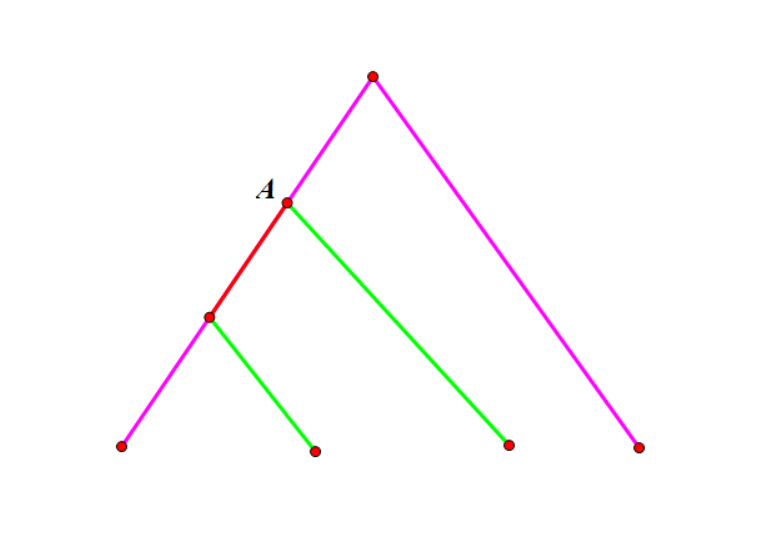
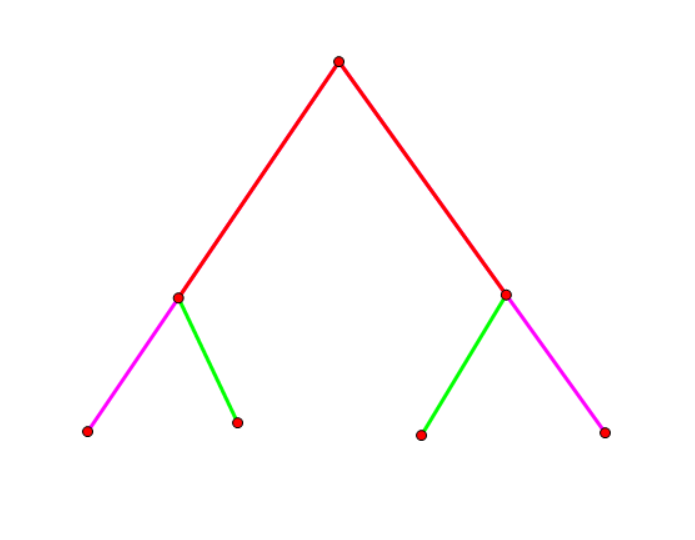
考虑如何计算它们的贡献,对于第一种情况,我们枚举两条路径 LCA 中深度较大者,也就是上图中的 A 点。枚举这个点 \(x\) 以后进而枚举对应的路径,设其为 \(u\to x\to v\),那么我们考虑二分重叠部分的长度 \(len\),那么这个重叠部分要么是 \(u\) 的 \(dep_u-dep_x-len\) 级祖先 \(fu\) 到 \(x\) 的路径,要么是 \(v\) 的 \(dep_v-dep_x-len\) 级祖先 \(fv\) 到 \(x\) 的路径,因此我们需要检验是否存在一条路径经过 \(fu\to x\) 上所有点或者经过 \(fv\to x\) 上所有点。我们考虑用线段树,维护一个端点在 \(x\) 子树内,一个端点不在 \(x\) 子树内的路径。具体来说我们求出每个点的 DFS 序 \(dfn_x\),对于线段树上下标为 \(p\) 的位置,我们存有多少条路径 \((u,v)\),满足 \(dfn_u=x\),且 \(u\) 在 \(x\) 子树内,\(v\) 在 \(x\) 子树外,这样检验时只需做一遍区间求和。那么怎么维护这个线段树呢?我们考虑对于每条路径,在 \(u\) 处的线段树上下标为 \(dfn_u\) 的位置上加一,\(v\) 处的线段树上下标为 \(dfn_v\) 的位置上加一,\(\text{LCA}(u,v)\) 处线段树上 \(dfn_u,dfn_v\) 位置上各减一,然后线段树合并即可。
对于第二种情况,我们考虑在两条路径交界处(也就是上图中粉色、绿色线段的上端点,红色线段的下段点)处统计贡献,我们还是对整棵树进行一遍 DFS 并枚举对应的点 \(x\),那么可以发现,如果我们把一个端点在 \(x\) 子树内,一个端点在子树外的路径拎出来并按照它们在子树外的端点的 DFS 序从小到大排序,最优的一对路径在排好序的序列中肯定是相邻的,因此我们考虑将所有路径压入一个 set,每次加入一棵子树时启发式合并,将大小小的 set 中元素暴力插入大小大的 set 中,插入时在 set 中 lower_bound 中找到 DFS 序与其相邻的点更新答案即可。
时间复杂度 \(n\log^2n\)。
const int MAXN=2e5;
const int LOG_N=19;
int n,k,hd[MAXN+5],nxt[MAXN+5],to[MAXN+5],ec=0,cc[MAXN+5];
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int dfn[MAXN+5],tim,edt[MAXN+5];
int dep[MAXN+5],top[MAXN+5],siz[MAXN+5],wson[MAXN+5];
int fa[LOG_N+2][MAXN+5];
void dfs01(int x){
siz[x]=1;dfn[x]=++tim;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];dep[y]=dep[x]+1;dfs01(y);siz[x]+=siz[y];
if(siz[y]>siz[wson[x]]) wson[x]=y;
} edt[x]=tim;
}
void dfs02(int x,int tp){
top[x]=tp;if(wson[x]) dfs02(wson[x],tp);
for(int e=hd[x];e;e=nxt[e]) if(to[e]^wson[x]) dfs02(to[e],to[e]);
}
int getlca(int x,int y){
while(top[x]^top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[0][top[x]];
} return (dep[x]<dep[y])?x:y;
}
struct dat{int a,b,lc,dis;} c[MAXN+5];
int get_kanc(int x,int k){
for(int i=LOG_N;~i;i--) if(k>>i&1) x=fa[i][x];
return x;
}
namespace segtree{
const int MAXP=MAXN*40;
struct node{int ch[2],val;} s[MAXP+5];
int rt[MAXN+5],ncnt=0;
void pushup(int k){s[k].val=s[s[k].ch[0]].val+s[s[k].ch[1]].val;}
void insert(int &k,int l,int r,int p,int v){
if(!k) k=++ncnt;if(l==r) return s[k].val+=v,void();
int mid=l+r>>1;
if(p<=mid) insert(s[k].ch[0],l,mid,p,v);
else insert(s[k].ch[1],mid+1,r,p,v);
pushup(k);
}
int query(int k,int l,int r,int ql,int qr){
if(!k) return 0;
if(ql<=l&&r<=qr) return s[k].val;
int mid=l+r>>1;
if(qr<=mid) return query(s[k].ch[0],l,mid,ql,qr);
else if(ql>mid) return query(s[k].ch[1],mid+1,r,ql,qr);
else return query(s[k].ch[0],l,mid,ql,mid)+query(s[k].ch[1],mid+1,r,mid+1,qr);
}
int merge(int x,int y,int l,int r){
if(!x||!y) return x+y;int z=++ncnt,mid=l+r>>1;
if(l==r) return s[z].val=s[x].val+s[y].val,z;
s[z].ch[0]=merge(s[x].ch[0],s[y].ch[0],l,mid);
s[z].ch[1]=merge(s[x].ch[1],s[y].ch[1],mid+1,r);
pushup(z);return z;
}
}
using segtree::rt;
using segtree::insert;
using segtree::query;
using segtree::merge;
vector<int> pth[MAXN+5];
vector<pii> add[MAXN+5],del[MAXN+5];
pair<int,int> mx_id1=mp(0,1);
pair<int,pii> mx_id2;
void dfs1(int x){
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];dfs1(y);
rt[x]=merge(rt[x],rt[y],1,n);
}
insert(rt[x],1,n,dfn[x],cc[x]);
for(int id:pth[x]){
insert(rt[x],1,n,dfn[c[id].a],-1);
insert(rt[x],1,n,dfn[c[id].b],-1);
if(c[id].dis<mx_id1.fi) continue;
if(c[id].a!=x){
int len=dep[c[id].a]-dep[x];
int l=1,r=dep[c[id].a]-dep[x],p=0;
while(l<=r){
int mid=l+r>>1,anc=get_kanc(c[id].a,len-mid);
if(query(rt[x],1,n,dfn[anc],edt[anc])) p=mid,l=mid+1;
else r=mid-1;
} chkmax(mx_id1,mp(p,id));
} if(c[id].b!=x){
int len=dep[c[id].b]-dep[x];
int l=1,r=dep[c[id].b]-dep[x],p=0;
while(l<=r){
int mid=l+r>>1,anc=get_kanc(c[id].b,len-mid);
if(query(rt[x],1,n,dfn[anc],edt[anc])) p=mid,l=mid+1;
else r=mid-1;
} chkmax(mx_id1,mp(p,id));
}
}
}
bool has_anc(int x,int y){//whether x and y are ancestor and son
return (getlca(x,y)==x)||(getlca(x,y)==y);
}
int calc_fa_son(int x1,int y1,int x2,int y2){//y1 is the ancestor of x1
int lc=getlca(x1,x2);
return max(dep[lc]-max(dep[y1],dep[y2]),0);
}
int calc(int x,int y){
if(x==y) return -1;
if(c[x].dis<mx_id2.fi) return 0;
if(c[y].dis<mx_id2.fi) return 0;
if(!has_anc(c[x].lc,c[y].lc)) return 0;
return calc_fa_son(c[x].a,c[x].lc,c[y].a,c[y].lc)+
calc_fa_son(c[x].b,c[x].lc,c[y].a,c[y].lc)+
calc_fa_son(c[x].a,c[x].lc,c[y].b,c[y].lc)+
calc_fa_son(c[x].b,c[x].lc,c[y].b,c[y].lc);
}
set<pii> stv[MAXN+5];
bool ban[MAXN+5];
void upd_ans(int x,int y){chkmax(mx_id2,mp(calc(x,y),mp(x,y)));}
void ins_st(set<pii> &st,pii p){
if(c[p.se].dis<mx_id2.fi) return ban[p.se]=1,void();
else{
set<pii>::iterator it=st.upper_bound(p);
if(it!=st.end()) upd_ans(p.se,it->se);
if(it!=st.begin()) upd_ans(p.se,(--it)->se);
st.insert(p);
}
}
void dfs2(int x){
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];dfs2(y);
if(stv[y].size()>stv[x].size()) stv[x].swap(stv[y]);
for(pii p:stv[y]) ins_st(stv[x],p);
}
for(pii p:add[x]) ins_st(stv[x],mp(dfn[p.fi],p.se));
for(pii p:del[x]) if(!ban[p.se])
stv[x].erase(stv[x].find(mp(dfn[p.fi],p.se)));
}
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=2,f;i<=n;i++) scanf("%d",&f),adde(f,i),fa[0][i]=f;
dfs01(1);dfs02(1,1);
for(int i=1;i<=LOG_N;i++) for(int j=1;j<=n;j++) fa[i][j]=fa[i-1][fa[i-1][j]];
for(int i=1;i<=k;i++){
scanf("%d%d",&c[i].a,&c[i].b);
c[i].lc=getlca(c[i].a,c[i].b);
if(c[i].lc!=c[i].a&&c[i].lc!=c[i].b) pth[c[i].lc].pb(i);
cc[c[i].a]++;cc[c[i].b]++;
add[c[i].a].pb(mp(c[i].b,i));
add[c[i].b].pb(mp(c[i].a,i));
del[c[i].lc].pb(mp(c[i].a,i));
del[c[i].lc].pb(mp(c[i].b,i));
c[i].dis=dep[c[i].a]+dep[c[i].b]-(dep[c[i].lc]<<1);
} dfs1(1);
for(int i=1;i<=k;i++) if(i^mx_id1.se)
chkmax(mx_id2,mp(calc(i,mx_id1.se),mp(i,mx_id1.se)));
dfs2(1);
printf("%d\n%d %d\n",mx_id2.fi,mx_id2.se.fi,mx_id2.se.se);
return 0;
}
/*
7 2
1 1 2 2 3 3
4 7
5 6
*/




 浙公网安备 33010602011771号
浙公网安备 33010602011771号