Codeforces 666D - Chain Reaction（分类讨论）

Codeforces 题目传送门 & 洛谷题目传送门

大分类讨论题 /qd

首先我们称左上、右上、右下、左下分别 \(0,1,2,3\) 号点，我们枚举这四个点分别对应输入中的哪个点，这部分 \(4!\)。

接下来我们枚举四个点分别是左右移动还是上下移动，这部分共有 \(16\) 种情况，但是仔细想一下只用分三类：

1. 螺旋状，即下图（还有一种情况没画出来）

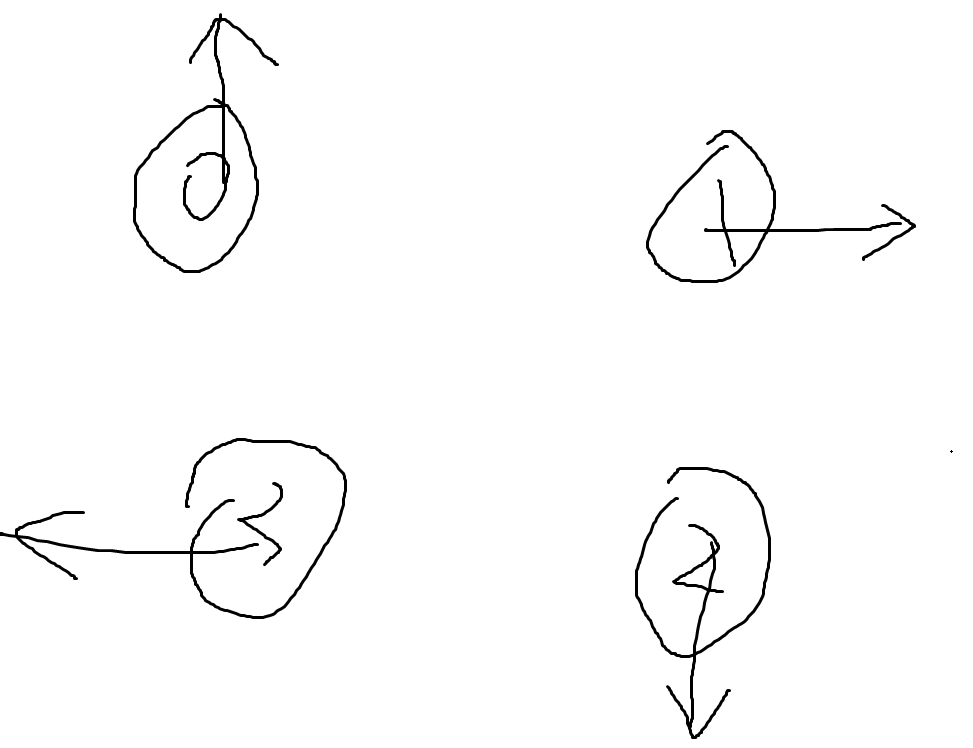
显然，由于 \(1\) 的 \(y\) 轴坐标不变，而 \(0,1\) 最终的 \(y\) 坐标相同，所以我们可以直接得到 \(0\) 的 \(y\) 坐标，同理 \(1,2\) 最终的 \(x\) 坐标相同，因此我们可以得到 \(1\) 的 \(x\) 坐标，这样我们可以还原出四个点最终的坐标，直接判定即可。

2. 直线状（即所有点都在上下方向运动，要么都往左右方向运动）

   这里以都在上下方向运动为例，显然如果 \(1,2\) 横坐标不同，或者 \(0,3\) 横坐标不同就直接 GG 了。否则我们可以求出正方形的边长 \(A=x_1-x_0\)，这样相当于我们要找一个合适的 \(Y\) 使得 \(\max{|y_0-(Y+A)|,|y_1-(Y+A)|,|y_2-Y|,|y_3-Y|}\) 最小，这是经典问题，招待 \(y_0-A,y_1-A,y_2,y_3\) 四者的最大值和最小值，取个平均数即可。

3. 其他

   

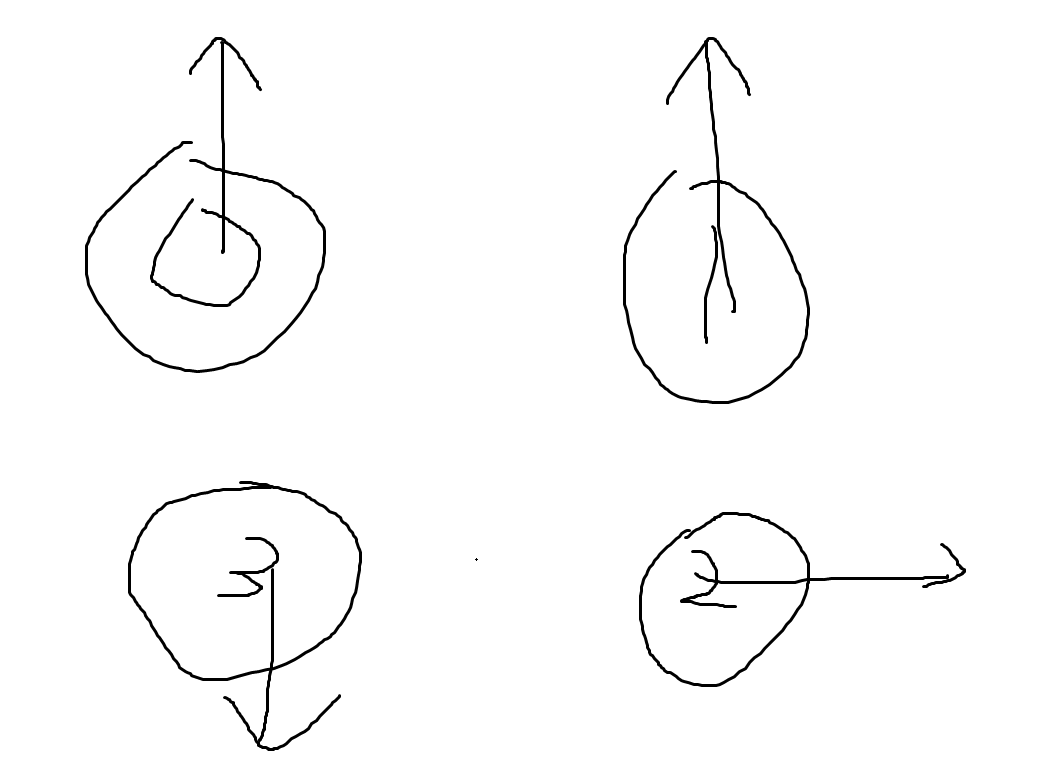
   我们找到一对相邻的点，使得最终它们 \(y\) 坐标相同且都在上下方向运动，或者它们 \(x\) 坐标相同且都在左右方向运动（在上面的例子中为 \(0,1\)，由于我们特判掉了前面的情况所以必然存在这一对点），那么正方形的边长也确定了，就是 \(0,1\) 横坐标之差，我们再在另外两个点中找到一个在左右方向上运动的（也必然能够找得到），比方说是 \(2\)，那么我们可以确定 \(2\) 最终的 \(y\) 坐标（保持不变），又根据正方形边长为 \(x_1-x_0\) 我们可以知道 \(0,1\) 最终的 \(y\) 坐标，而 \(1,2\) 在同一 \(x\) 坐标处又可得出 \(2\) 的 \(x\) 坐标，这样 \(3\) 最终的坐标就直接出来了。

使用旋转坐标系可以减小代码量。

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
template<typename T1, typename T2> void chkmin(T1 &x, T2 y) {if (x > y) x = y;}
template<typename T1, typename T2> void chkmax(T1 &x, T2 y) {if (x < y) x = y;}
int x[5], y[5], p[5], mn = 1e9, resx[5], resy[5];
int calc(int X[4], int Y[4], int P[4]) {
	if (Y[0] != Y[1] || Y[2] != Y[3] || X[1] != X[2] || X[3] != X[0]) return 1e9;
	for (int i = 0; i < 4; i++) if (abs(X[i] - X[(i + 1) & 3]) + abs(Y[i] - Y[(i + 1) & 3]) != abs(X[0] - X[1])) return 1e9;
	if (X[0] == X[1]) return 1e9;
	for (int i = 0; i < 4; i++) {
		int sum = (X[i] == x[P[i]]) + (Y[i] == y[P[i]]);
		if (sum == 0) return 1e9;
	}
	int mx = 0;
	for (int i = 0; i < 4; i++) chkmax(mx, abs(X[i] - x[P[i]]) + abs(Y[i] - y[P[i]]));
	return mx;
}
void solve() {
	memset(resx, 0, sizeof(resx)); memset(resy, 0, sizeof(resy)); mn = 1e9;
	for (int i = 0; i < 4; i++) scanf("%d%d", &x[i], &y[i]);
	for (int rv = 0; rv < 2; rv++) {
		for (int i = 0; i < 4; i++) p[i] = i;
		do {
			for (int msk = 0; msk < 16; msk++) {
				static int nwx[5], nwy[5];
				auto upd = [&](int cst) {
					if (mn > cst) {
						mn = cst;
						for (int i = 0; i < 4; i++) {
							if (!rv) resx[p[i]] = nwx[i], resy[p[i]] = nwy[i];
							else resx[p[i]] = nwy[i], resy[p[i]] = nwx[i];
						}
					}
				};
				for (int i = 0; i < 4; i++) nwx[i] = x[p[i]], nwy[i] = y[p[i]];
				if (msk == 10) {
					nwy[0] = y[p[1]]; nwx[1] = x[p[2]]; nwy[2] = y[p[3]]; nwx[3] = x[p[0]];
					upd(calc(nwx, nwy, p));
				} else if (msk == 0) {
					int A = x[p[1]] - x[p[0]];
					vector<int> vec; vec.pb(y[p[0]] - A); vec.pb(y[p[1]] - A); vec.pb(y[p[2]]); vec.pb(y[p[3]]);
					sort(vec.begin(), vec.end()); int dw = vec[0] + vec[3] >> 1, up = dw + A;
					nwy[0] = nwy[1] = up; nwy[2] = nwy[3] = dw;
					upd(calc(nwx, nwy, p));
				} else {
					if ((~msk & 1) && (~msk >> 1 & 1)) {
						int A = abs(nwx[0] - nwx[1]);
						for (int i = 2; i <= 3; i++) if (msk >> i & 1) {
							nwx[i] = nwx[3 - i]; nwy[i ^ 1] = nwy[i];
							nwy[0] = nwy[1] = nwy[i] + A; nwx[i ^ 1] = nwx[3 - (i ^ 1)];
							break;
						}
						upd(calc(nwx, nwy, p));
					} else if ((~msk >> 2 & 1) && (~msk >> 3 & 1)) {
						int A = abs(nwx[3] - nwx[2]);
						for (int i = 0; i <= 1; i++) if (msk >> i & 1) {
							nwx[i] = nwx[3 - i]; nwy[i ^ 1] = nwy[i];
							nwy[2] = nwy[3] = nwy[i] - A; nwx[i ^ 1] = nwx[3 - (i ^ 1)];
							break;
						}
						upd(calc(nwx, nwy, p));
					}
				}
			}
		} while (next_permutation(p, p + 4));
		for (int i = 0; i < 4; i++) swap(x[i], y[i]);
	}
	if (mn > 200000000) puts("-1");
	else {
		printf("%d\n", mn);
		for (int i = 0; i < 4; i++) printf("%d %d\n", resx[i], resy[i]);
	}
}
int main() {int qu; scanf("%d", &qu); while (qu--) solve(); return 0;}