2021.10.11 模拟赛题解

T1

记 \(S=A_0+B_0,T=B_0+A_0\)，那么不难发现 \(A_{935}\) 是由 \(S,T\) 交替拼接而成的，并且打个表可以发现这东西形如 \(STTSTSSTTSST...\)，稍微敏感的同学可以发现对于第 \(i\) 位（下标从 \(0\) 开始），如果 \(i\) 二进制中 \(1\) 的个数是奇数，那么第 \(i\) 个字符串是 \(T\)，否则第 \(i\) 个字符串是 \(S\)，那么直接调用 C++ 头文件库里的 __builtin_parityll 即可知道 \(x\) 所在的周期究竟是 \(S\) 还是 \(T\)。

事实上这种字符串可以用来卡 u64 哈希哦（

T2

考虑 Kruskal 的过程。对于边权为 \(w\) 的边，如果边权为 \(w\) 的边不在最小生成树中，那么假设最小生成树中边权 \(<w\) 的边有 \(k\) 条，把这 \(k\) 条边连起来后形成的连通块大小分别是 \(s_1,s_2,\cdots,s_m\)，那么显然边权为 \(w\) 的边只能连在这 \(m\) 个连通块中某个连通块的两个点之间并且不能与已经连的边重合，方案数就是 \(\sum\limits_{i=1}^m\dfrac{s_i(s_i-1)}{2}-k\)，把它们乘起来即可，输出方案就用个队列记录一下可行的边集即可。

时间复杂度 \(n^2\)。

T3

完蛋了不会容斥了/dk

题解链接

T4

一个很显然的想法是对于每个障碍组成的线段，求出以其为对角线的正方形，答案就是这些正方形的面积并，但是这个做法连样例一都过不去/qd

观察样例可以发现，如果两条线段对应的正方形相交，并且相交情况形如下面第一张图，那么左右两边的凹陷部分也是 Wave 所不能经过的，但如果两条线段所对应的正方形相交情况如下面第二幅图，那么上下的凹陷部分是不用补的：

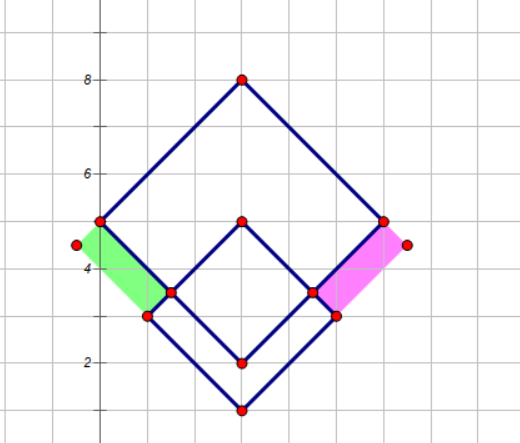
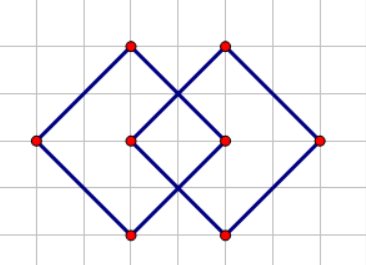
因此我们考虑对于未被计算的部分，新建一些图形使其能够恰好覆盖它们，然后再求一遍矩形面积并即可得到真正的答案。于是问题就转化为如何补全它们，我们考虑将每个正方形从中间一分为二裂成两个等腰直角三角形，这样每次补全一个图形，就等价于伸长某个等腰直角三角形的斜边。这里我们考虑对补全左边的等腰直角三角形和补全右边的等腰直角三角形分别考虑，以左边为例，注意到如果我们将线段按 \(x\) 排序，那么只可能出现右边的线段使左边的等腰直角三角形斜边伸长，并且如果我们关于等腰直角三角形两个非直角顶点做 \(y=x\) 的平行线，设其与 \(y\) 轴两个交点纵坐标分别为 \(l_i,r_i\)，那么一个线段 \(i\) 能够使线段 \(j\) 的斜边（\(x_i\ge x_j\)）伸长，当且仅当 \([l_i,r_i]\) 与 \([l_j,r_j]\) 有交但又不是包含关系，因此我们考虑用一个线段树维护 \(l_j\in[l_i,r_i]\) 的 \(r_j\) 的最大值，以及 \(r_j\in[l_i,r_i]\) 的 \(l_j\) 的最小值，即可知道线段 \(i\) 的斜边会延伸到什么。对于右侧也同理，于是问题转化为求 \(2m\) 个等腰直角三角形的面积并，这个是不好维护的，不过注意到同一线段延伸出去的两个等腰直角三角形，它们斜边肯定是有重合部分的，并且我们能够证明，将它们的斜边都变为它们原来斜边的并不会影响答案，因此我们可以将等腰直角三角形改为斜向的正方形，而斜向的正方形的面积并是好求的，旋转下坐标系即可转化为普通的面积并问题，扫描线+线段树即可解决。由于此题坐标范围不大，因此不用离散化。

时间复杂度 \(m\log m\)。

作为本场比赛最毒瘤的题，就给个代码罢（

const int MAXN=2e5;
const int MAXV=5e5;
int n;
struct dat{
	int x,l,r,id;
	bool operator <(const dat &rhs){
		if(x^rhs.x) return x<rhs.x;
		if(r^rhs.r) return r<rhs.r;
		return l<rhs.l;
	}
} a[MAXN+5];
pii lft[MAXN+5],rit[MAXN+5];
struct S1{
	int op;//0 for min and 1 for max
	struct node{int l,r,val;} s[MAXV*3+5];
	void pushup(int k){
		if(op) s[k].val=max(s[k<<1].val,s[k<<1|1].val);
		else s[k].val=min(s[k<<1].val,s[k<<1|1].val);
	}
	void build(int k,int l,int r){
		s[k].l=l;s[k].r=r;s[k].val=(op)?(-INF):INF;if(l==r) return;
		int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);
	}
	void modify(int k,int p,int x){
		if(s[k].l==s[k].r){
			if(op) chkmax(s[k].val,x);
			else chkmin(s[k].val,x);
			return;
		} int mid=s[k].l+s[k].r>>1;
		(p<=mid)?modify(k<<1,p,x):modify(k<<1|1,p,x);
		pushup(k);
	}
	int query(int k,int l,int r){
		if(l<=s[k].l&&s[k].r<=r) return s[k].val;
		int mid=s[k].l+s[k].r>>1;
		if(r<=mid) return query(k<<1,l,r);
		else if(l>mid) return query(k<<1|1,l,r);
		else{
			if(op) return max(query(k<<1,l,mid),query(k<<1|1,mid+1,r));
			else return min(query(k<<1,l,mid),query(k<<1|1,mid+1,r));
		}
	}
} mn,mx;
vector<pair<pii,int> > op[MAXV*2+10];
bool vis[2005][2005];
void addbar(int x1,int y1,int x2,int y2){
//	printf("add %d %d %d %d\n",x1,y1,x2,y2);
	op[x1+MAXV].pb(mp(mp(y1,y2-1),1));
	op[x2+MAXV].pb(mp(mp(y1,y2-1),-1));
}
struct S2{
	struct node{int l,r,mn,cnt,lz;} s[MAXV*8+10];
	void pushup(int k){
		s[k].mn=min(s[k<<1].mn,s[k<<1|1].mn);s[k].cnt=0;
		if(s[k].mn==s[k<<1].mn) s[k].cnt+=s[k<<1].cnt;
		if(s[k].mn==s[k<<1|1].mn) s[k].cnt+=s[k<<1|1].cnt;
	}
	void build(int k,int l,int r){
		s[k].l=l;s[k].r=r;if(l==r) return s[k].mn=0,s[k].cnt=1,void();
		int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);pushup(k);
	}
	void tag(int k,int v){s[k].mn+=v;s[k].lz+=v;}
	void pushdown(int k){if(s[k].lz) tag(k<<1,s[k].lz),tag(k<<1|1,s[k].lz),s[k].lz=0;}
	void modify(int k,int l,int r,int v){
		if(l>r) return;
//		printf("modify %d %d %d %d\n",k,l,r,v);
		if(l<=s[k].l&&s[k].r<=r) return tag(k,v),void();
		pushdown(k);int mid=s[k].l+s[k].r>>1;
		if(r<=mid) modify(k<<1,l,r,v);
		else if(l>mid) modify(k<<1|1,l,r,v);
		else modify(k<<1,l,mid,v),modify(k<<1|1,mid+1,r,v);
		pushup(k);
	}
	int query(){return (s[1].mn>0)?(MAXV*2+1):(MAXV*2+1-s[1].cnt);}
} st;
int main(){
	freopen("yoshino.in","r",stdin);
	freopen("yoshino.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&a[i].x,&a[i].l,&a[i].r);
		a[i].id=i;lft[i]=rit[i]=mp(a[i].l,a[i].r);
	} sort(a+1,a+n+1);reverse(a+1,a+n+1);mn.op=0;mx.op=1;
	mn.build(1,-100000,200000);mx.build(1,-100000,200000);
	for(int i=1;i<=n;i++){
		chkmax(lft[a[i].id].se,mx.query(1,a[i].l+a[i].x,a[i].r+a[i].x)+a[i].x);
		chkmin(lft[a[i].id].fi,mn.query(1,a[i].l-a[i].x,a[i].r-a[i].x)-a[i].x);
		mx.modify(1,lft[a[i].id].fi+a[i].x,lft[a[i].id].se-a[i].x);
		mn.modify(1,lft[a[i].id].se-a[i].x,lft[a[i].id].fi+a[i].x);
	}
	for(int i=1;i<=n;i++) a[i].x=100000-a[i].x;
	sort(a+1,a+n+1);reverse(a+1,a+n+1);mn.op=0;mx.op=1;
	mn.build(1,-100000,200000);mx.build(1,-100000,200000);
	for(int i=1;i<=n;i++){
		chkmax(rit[a[i].id].se,mx.query(1,a[i].l+a[i].x,a[i].r+a[i].x)+a[i].x);
		chkmin(rit[a[i].id].fi,mn.query(1,a[i].l-a[i].x,a[i].r-a[i].x)-a[i].x);
		mx.modify(1,rit[a[i].id].fi+a[i].x,rit[a[i].id].se-a[i].x);
		mn.modify(1,rit[a[i].id].se-a[i].x,rit[a[i].id].fi+a[i].x);
	}
	for(int i=1;i<=n;i++) a[i].x=100000-a[i].x;
//	for(int i=1;i<=n;i++) printf("%d %d %d %d\n",lft[i].fi,lft[i].se,rit[i].fi,rit[i].se);
	for(int i=1;i<=n;i++){
		int L=min(lft[a[i].id].fi,rit[a[i].id].fi);
		int R=max(lft[a[i].id].se,rit[a[i].id].se);
		addbar(a[i].x-R,a[i].x+L,a[i].x-L,a[i].x+R);
	} st.build(1,-MAXV,MAXV);ll res=0;
	for(int i=-MAXV;i<=MAXV;i++){
		for(pair<pii,int> p:op[i+MAXV]) st.modify(1,p.fi.fi,p.fi.se,p.se);
		res+=st.query();
	}
	printf("%lld.%lld0\n",res>>1,(res&1)*5);
	return 0;
}
/*
3
0 1 2
0 2 3
0 3 4
*/