2-DP_题解
2-DP_题解
A,不要62_前缀和
题目大意
中文题
思路和代码
初始化一个前缀和数组表示[1,i]之间有多少有效车牌即可
ll l , r ;
ll p[N] ;
ll ck(ll x){
ll y = x ;
while(y){
int t = y % 10 ;
if(t == 4) return 0 ;
if(t == 2){
t = y / 10 % 10 * 10 + t ;
if(t == 62) return 0 ;
}
y /= 10 ;
}
return 1 ;
}
int main(){
// freopen("in.in" , "r" , stdin) ;
ios::sync_with_stdio(false) ;
cin.tie(0) ; cout.tie(0) ;
rep(i , 1 , 1e6 + 10){
p[i] = p[i - 1] + ck(i) ;
}
while(1){
cin >> l >> r ;
if(!l && !r) break ;
cout << p[r] - p[l - 1] << "\n" ;
}
}//code_by_tyrii
B,Constanze's Machine
题目大意
给一个串,其中不能出现w或m。w被uu代替,m被nn代替。现在问该串最多有几种含义。
思路和代码
方法一:
以“uuuuuu”举例,下图每个圈都是一个u,画红线表示uu组合成w。设fi为长度为i的全u或全v的种数。
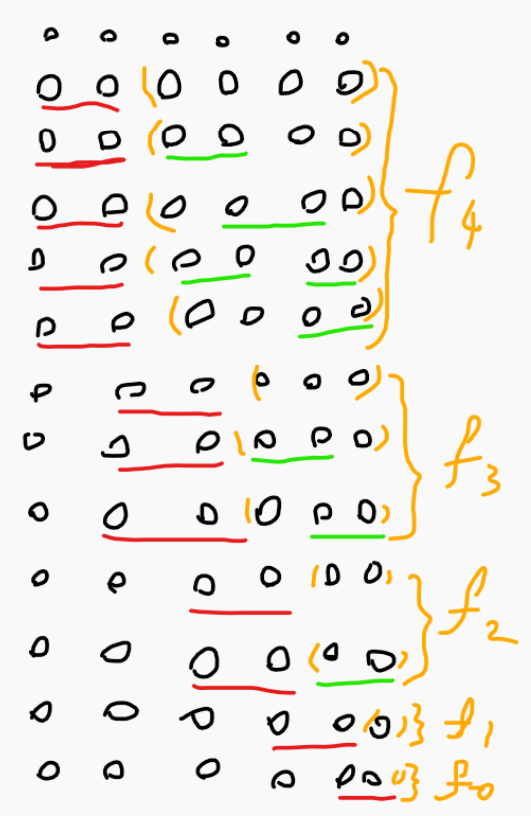
可以发现长度为k的全u或者全v可以由以下式子算出答案:
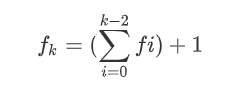
所以双指针找出所有全u或全v的区间,利用fi即可得到答案。
int n , m , k ;
bool ck(ll x , string &s){
if((s[x] != 'u' && s[x] != 'n') || x == n) return 0 ;
if(s[x] != s[x + 1]) return 0 ;
return 1 ;
}
ll f[N] ;
void solve(){
string s ;
cin >> s ;
s = " " + s ;
ll ans = 1 ;
n = s.size() - 1 ;
f[0] = f[1] = 1 ;
f[2] = 2 ;
f[3] = 3 ;
ll sum = 4 ;
rep(i , 4 , n){
sum = (sum + 1) % mod ;
f[i] = sum ;
sum = (sum + f[i - 1]) % mod ;
}
rep(i , 1 , n) cout << f[i] << " \n"[i == n] ;
rep(i , 1 , n)
if(s[i] == 'm' || s[i] == 'w'){
cout << "0\n" ; return ;
}
ll l = 1 , r = 1 ;
while(l <= n && r <= n){
while(l <= n && !ck(l , s)) l ++ ;
// cout << l << "\n" ;
if(l > n) break ;
r = l + 1 ;
while(r <= n && s[r] == s[l]) r ++ ;
// cout << l << " " << r << "\n" ;
ans = (ans * f[r - l]) % mod ;
l = r ;
}
cout << ans << "\n" ;
}//code_by_tyrii
法二:
对于长度为L的全u或全v串来说,如果再加上一个一样的字符,则会变成以下情况:
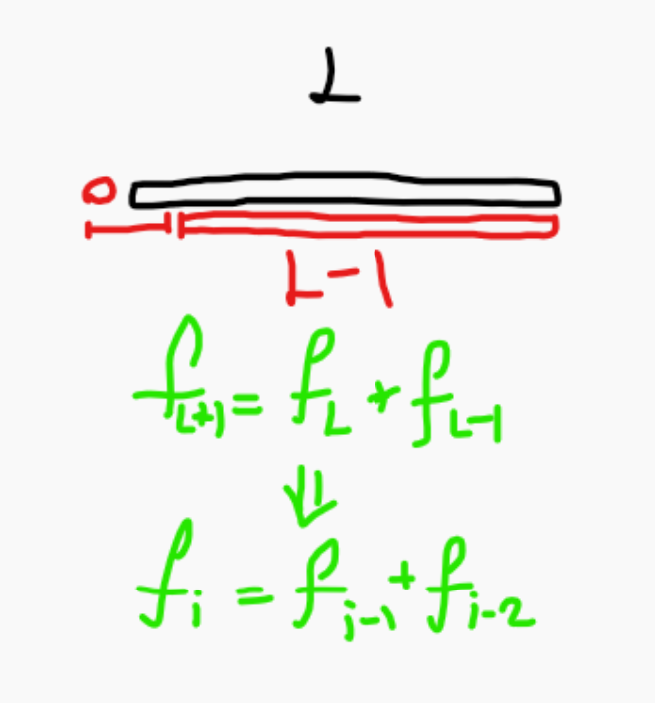
所以之前代码的f初始化就可以直接改为fibonacci数列。(代码略)
C,Bellovin_LIS
题目大意
给一个数列a,F(a)i 表示以ai结尾的LIS(最长上升子序列)的长度。现在要找到字典序最小的数列b,使得F(a)=F(b)
思路和代码
这题是LIS模板,代码建议保存。
设置ans数组,ansi表示以ai结尾的LIS长度。
可以发现最优的数列b就是ans数组。因为ans1一定是1,整个数列的字典序一定是最小的。所以题目就转化为以O(nlogn)复杂度求LIS。
下面给出模板。
void solve(){
cin >> n ;
vct<ll> dp(n + 1 , INF) ;
vct<ll> ans(n + 1 , 0) ;
rep(i , 1 , n){
ll t ; cin >> t ;
ll idx = lower_bound(all(dp) , t) - dp.begin() ;
dp[idx] = t ;
ans[i] = idx + 1 ;
}
rep(i , 1 , n) cout << ans[i] << " \n"[i == n] ;
}//code_by_tyrii
D,最长公共子序列_LIS
题目大意
中文
思路和代码
正常做LCS问题,需要n2的dp完成,但是这题数据范围1e5,就不能用n2的方法。题中给了一个条件,n个数字是n的排列。这一限制就可以用另外一种思路。
我们只要设置idx数组,表示x在a数组中的位置,然后对idx[bi]求LIS即可。这道题目比较巧妙的将LCS问题转化成了LIS问题。
void solve(){
cin >> n ;
vct<ll> idx(n + 1 , 0 ) ;
rep(i , 1 , n){
ll t ; cin >> t ;
idx[t] = i ;
}
vct<ll> dp(n + 1 , INF) ;
vct<ll> ans(n + 1 , 0) ;
rep(i , 1 , n){
ll t ; cin >> t ;
ll j = lower_bound(all(dp) , idx[t]) - dp.begin() ;
dp[j] = idx[t] ;
ans[i] = j + 1 ;
}
// rep(i , 1 , n) cout << ans[i] << " \n"[i == n] ;
cout << *max_element(all(ans)) << "\n" ;
}//code_by_tyrii
D,导弹拦截_贪心
题目大意
中文题
思路和代码
这道题就是要把所有的导弹分成两堆,一堆用第一个装置来拦截,另一堆用第二个装置来拦截。而拦截导弹具有单调性,拦截了远的导弹就可以把近的也一起拦截掉。所以用到第一个装置的距离降序排序,[i,n]部分由装置1拦截,[1,i-1]部分由装置2拦截即可。
void solve(){
ll x1 , x2 , y1 , y2 , n ;
cin >> x1 >> y1 >> x2 >> y2 >> n ;
vct<missile> a(n + 1) ;
rep(i , 1 , n){
ll tx , ty ;
cin >> tx >> ty ;
a[i].to1 = getdis(x1 , y1 , tx , ty) ;
a[i].to2 = getdis(x2 , y2 , tx , ty) ;
}
sort(a.begin() + 1 , a.end() , cmp) ;
ll ans = INF ;
ll m = -INF ;
ans = a[1].to1 ;
rep(i , 1 , n - 1){
m = max(a[i].to2 , m) ;
ans = min(ans , a[i+1].to1+m ) ;
}
cout << ans << "\n" ;
}//code_by_tyrii
G,石子合并
题目大意
中文
思路和代码
入门区间dp,不过是在一个环上进行的。把环断开成链即可,这里不多赘述。
ll n , m , k ;
ll a[N] ;
ll p[N] ;
ll ansmin = INF ;
ll ansmax = -INF ;
void DP(ll a[]){
ll dpmax[N][N] = {} ;
ll dpmin[N][N] = {} ;
rep(i , 1 , n)
rep(j , i , n) dpmin[i][j] = INF ;
rep(i , 1 , n) dpmin[i][i] = 0 ;
rep(i , 1 , n) p[i] = p[i - 1] + a[i] ;
rep(L , 1 , n)
for(int i = 1 ; i + L - 1 <= n ; i ++ ){
int j = i + L - 1 ;
rep(k , i , j - 1){
dpmax[i][j] = max(dpmax[i][j] , dpmax[i][k] + dpmax[k + 1][j] + p[j] - p[i - 1]) ;
dpmin[i][j] = min(dpmin[i][j] , dpmin[i][k] + dpmin[k + 1][j] + p[j] - p[i - 1]) ;
}
}
ansmax = max(ansmax , dpmax[1][n]) ;
ansmin = min(ansmin , dpmin[1][n]) ;
}
void solve(){
cin >> n ;
rep(i , 1 , n) cin >> a[i] ;
rep(j , n + 1 , 2 * n) a[j] = a[j - n] ;
rep(i , 1 , n){
ll b[N] = {} ;
rep(j , i , i + n - 1) b[j - i + 1] = a[j] ;
DP(b) ;
}
cout << ansmin << "\n" << ansmax << "\n" ;
}//code_by_tyrii




 浙公网安备 33010602011771号
浙公网安备 33010602011771号