通过数字三角形理解dp和搜索
数字三角形
题目大意:
给定一个数字三角形,从顶部出发,在每一结点可以移动至其左下方或右下方,一直走到底层,求最大的和。
思路:
一拿到题目就会想到贪心去做,就跟着题目去模拟一遍:
void dfs(int i , int j ){
ans += a[i][j] ;
if(i == n)return ;
if(a[i + 1][j + 1] > a[i + 1][j])dfs(i + 1 , j + 1 ) ;
else dfs(i + 1 , j ) ;//下和左下哪里大走哪里
}
但是这样做是错误的,因为这样模拟只考虑了当前节点的下一步节点的大小。而正确的做法是要在当前节点考虑以下一步节点为起点,走到第n行的整条路径之和的大小。这再次证明了贪心很多时候不是最优解,只是较优解。贪心虽好想,但特别容易WA
我们在面对岔路的时候,不可能不走一遍而是预见未来一样地知道走哪条路更优。我们需要两条路都走一遍。搜索就是这样的思想。给出朴素做法搜索代码:
int dfs(int i , int j ){
if(i == n)return a[i][j] ;
return a[i][j] + max(dfs(i + 1 , j) , dfs(i + 1 , j + 1)) ;
}//遇到岔路不知道怎么办,先走一遍再比较
以上两种代码的区别就是,第一个比较的是节点,第二个比较的是整条路径。这很关键。
我们的朴素做法在走到每一个节点都要去两次走到底,以此来判断更优的走法。但是这样,时间复杂度会达到n^3。是很不理想的。比如说,以同一个节点为起点会被两次访问到。如下图绿色和红色区域重叠发部分:
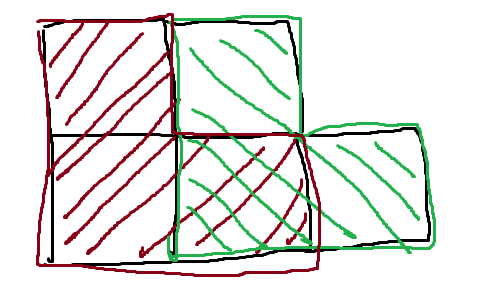
那如何解决重复访问的问题呢?下面给出两种方法:
记忆化搜索
记忆化搜索就是,在走到岔路的时候,依旧先向底层走一遍,走完的时候也是跟朴素做法一样返回。只不过在返回的过程中,将以每一个点为起点最后一层为终点的所有路径中的最优值记录下来,下次再遇到这个点就可以直接访问数据而不用重复走一遍。给出代码:
int dfs(int i , int j){
if(dp[i][j])return dp[i][j] ;//走过了就直接返回最优数据
if(i == n)return dp[i][j] = a[i][j] ;//走到最底层
return dp[i][j] = a[i][j] + max(dfs(i + 1 , j) , dfs(i + 1 , j + 1)) ;
}
这样时间复杂度就会大大降低。
动态规划
不论是朴素搜索还是记忆化搜索,都是在遇到岔路的时候先把两种方向都走一遍再判断谁更优秀。也就是说,是从上往下再由下往上的过程。而这里的底层状态是已知的,即只有一个点的话,最大路径和就是自己。我们可以定义dp数组dp[i][j]为从第i层的第j个走到第n层的路径最大和。那么一个点所对应的最大路径和就是他下一步走到的点作为起点走到n层作为终点的两种路径最大和的较优那种。于是有状态转移方程:
dp[j] = a[i][j] + max(dp[j] , dp[j + 1]) ;
所以有完整代码:
for(int i = n ; i > 0 ; i -- )//从底层往上
for(int j = 1 ; j <= i ; j ++ )
dp[j] = a[i][j] + max(dp[j] , dp[j + 1]) ;
小结
比较记忆化搜索和动态规划两个过程,我们可以发现dp数组的含义是一模一样的。只是求解的方式不同,下面给出一张图帮助理解:
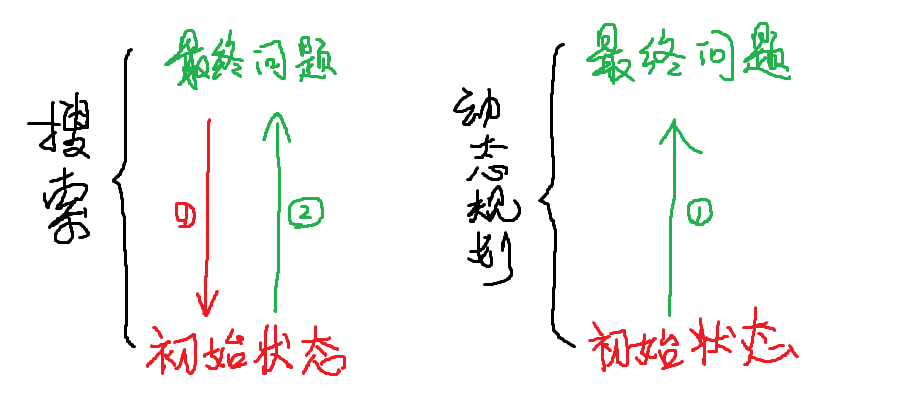


 浙公网安备 33010602011771号
浙公网安备 33010602011771号