单调队列专题1
单调队列专题1
题目来源:洛谷
写在前面:
学习单调队列一周了,许多概念还是似懂非懂。这导致了后面的题目越来越难以进行,对我的态度产生了比较大的消极影响。所以有必要将之前的题目仔细进行剖析,整理,分类。我题目做多了很容易陷入“划水”的状态,就是潜意识里抗拒仔细琢磨题解,潜意识里不想去看正确代码。这导致了我花费更多的时间,但是获得的收益反而比别人更低。接下来的总结分析我会从以下方面开展:
1、问题剖析分类
2、代码实现
3、实现过程的具体数据模拟(包括一般样例和边界样例)
4、和其他问题类型的解法比较
1.P2952 Cow Line S
0、题目大意:
有N头牛要排入一开始为空的队伍。AL是左边排入一头,AR是右边排入一头,DLK是左边离开K头,DRK是右边离开K头。问最后排队情况。
1、问题类型:
简单双端队列模拟
2、代码实现:
#include<bits/stdc++.h>
using namespace std;
int n , k , num ;
char op , x ;
deque<int>q ;
int main(){
cin>>n ;
for(int i = 1 ; i <= n ; i ++ ){//n次询问
cin>>op>>x ;
if(op == 'A'){
if(x == 'R'){
q.push_back(++num) ;//右插入
}else q.push_front(++num) ;//左插入
}else{
cin>>k ;
while(q.size() && k -- ){
if(x == 'R')q.pop_back() ;//右出队
else q.pop_front() ;//左出队
}
}
}
for(auto x : q)cout<<x<<"\n" ;
}
3、数据模拟和其他问题比较
这题就是单调队列的基本操作,没什么好说单调。
2、P1886 滑动窗口
0、题目大意:
n个数和一个长度为k的窗口,窗口的左端从1开始一位一位向右边滑动,问每一次滑动窗口中最大值和最小值。
1、问题类型:
滑动固定区间最值
2、代码实现:
#include<queue>
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6+500 ;
int n , k ;
int a[N] ;
deque<int >q ;
int main(){
cin>>n>>k ;
for(int i = 1 ; i <= n ; i ++ )cin>>a[i] ;
for(int i = 1 ; i <= n ; i ++ ){
while(q.size() && a[q.back()] >= a[i])q.pop_back() ;
q.push_back(i) ;//自己也可能是闭区间内最小值
while(q.size() && i - q.front() >= k)q.pop_front() ;
if(i >= k)cout<<a[q.front()]<<" ";
}//最小值,维护队头到队尾升序的单调队列
cout<<"\n" ;
q.clear() ;
for(int i = 1 ; i <= n ; i ++ ){
while(q.size() && a[q.back()] <= a[i])q.pop_back() ;
q.push_back(i) ;//自己也可能是闭区间内最大值
while(q.size() && i - q.front() >= k)q.pop_front() ;//过滤
if(i >= k)cout<<a[q.front()]<<" ";
}//最小值,维护队头到队尾降序的单调队列
}
3、数据模拟:
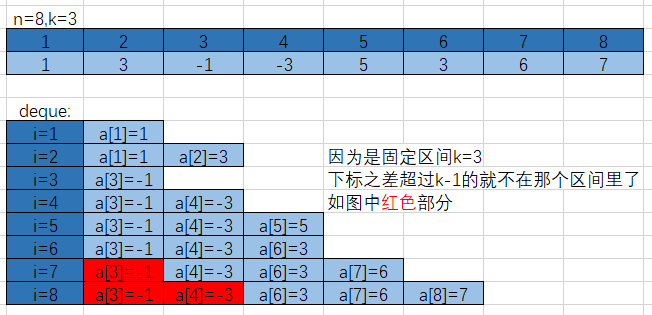
4、小结:
构造单调队列的时候可以无脑构造,我们取用最值的时候可以根据条件过滤一下(看代码注释)
3、P1638 逛画展
0、题目大意:
有n幅由m个大师画的图画,要找到一个最小的区间,区间中包含所有大师的画。
1、问题类型:
根据条件找区间问题
因为这个区间是有条件的,所以区间长度和该条件可以通过某种关系联系起来,这样就可以用尺取(双指针)的方法解题了。
2、代码实现:
以下是错误代码:
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6+500 ;
int n , m , num , ansl , ansr = 0x3f3f3f3f;
int a[N] ;
int b[N] ;//一个画家一个桶
int main(){
cin>>n>>m ;
for(int i = 1 ; i<= n ; i ++ )cin>>a[i] ;
int i = 1 , j = 2 ;
num = 1 ;
b[a[1]] = 1 ;
while(i <= n && j <= n ){//该while错误
if(!b[a[j]])num++ ;
b[a[j]]++ ;
if(num == m){
if(ansr - ansl > j - i){
ansr = j ;
ansl = i ;
}
b[a[i]]-- ;
if(!b[a[i]])num-- ;
i++ ;
}
j ++ ;
}
cout<<ansl<<" "<<ansr ;
}
错在内循环,每一次循环都将j指针右移。画家数量刚刚好是m时,i指针右移一位之后紧接着下一个循环中j指针就动了。而正解是,在j指针移到画家数量达到m时,i指针不断右移,一直移到画家数量等于m-1为止。然后j指针接着右移去找。正解如下:
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6+500 ;
int n , m , num , ansl , ansr = 0x3f3f3f3f;
int a[N] ;
int b[N] ;//一个画家一个桶
int main(){
cin>>n>>m ;
for(int i = 1 ; i<= n ; i ++ )cin>>a[i] ;
//限制区间长度的是画家数量m
//也就是说,只要画家数量到了m就是极限,根据这个来设计双指针程序
//画家未到m,j右移;画家到m,i右移
int i = 1 , j = 1 ;
while(i <= n && j <= n + 1){
if(num == m){
while(num == m){
if(ansr - ansl > (j - 1) - i){
ansr = j - 1;
ansl = i ;
}
b[a[i]] -- ;
if(!b[a[i]])num -- ;
i ++ ;
}
}else{
if(!b[a[j]])num ++ ;
b[a[j]] ++ ;
j ++ ;//这里j++,就是说如果此时num==m,那j是真正右边界的后一个
}
}
cout<<ansl<<" "<<ansr ;
}
那看到这里,聪明的同学就会问了,这双指针的东西和我们单调队列有什么关系啊?
我们这样想,双指针的左右指针i和j就相当于一个双端队列的front和back。 j不断右移就是队列不断从右入队,i不断右移就是队列不断从左出队。代码如下:
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6+500 ;
int n , m , num , ansl , ansr = 0x3f3f3f3f;
int a[N] ;
int b[N] ;//一个画家一个桶
deque<int>q ;
int main(){
cin>>n>>m ;
for(int i = 1 ; i<= n ; i ++ )cin>>a[i] ;
//限制区间长度的是画家数量m
//也就是说,只要画家数量到了m就是极限,根据这个来设计双指针程序
//画家未到m,j右移;画家到m,i右移
int i = 1 ;
while(i <= n + 1){
if(num == m){
while(num == m){
int idx = q.front() ;
q.pop_front() ;
if((i - 1) - idx < ansr - ansl){
ansr = i - 1 ;
ansl = idx ;
}
b[a[idx]]-- ;
if(!b[a[idx]])num -- ;
}
}else{
if(!b[a[i]])num ++ ;
b[a[i]] ++ ;
q.push_back(i ++ ) ;
}
}
cout<<ansl<<" "<<ansr ;
}
P2947 Look Up S
0、题目大意:
每头牛向右边看,输出第一个比他自己高的位置,若没有则出0 。
1、问题类型:
比他大的第一个数
2、代码实现
#include<bits/stdc++.h>
using namespace std ;
const int N = 1e6 + 50 ;
const int INF = 0x3f3f3f3f ;
int n ;
int a[N] , ans[N];
deque<int>q ;
int main(){
cin>>n ;
for(int i = 1 ; i <= n ; i ++ )cin>>a[i] ;
a[0] = INF ;
q.push_back(0) ;
for(int i = n ; i > 0 ; i -- ){//向右看倒序遍历
while(q.size() && a[i] >= a[q.front()])q.pop_front() ;
ans[i] = q.front() ;//构造一个栈顶到栈底升序单调栈
q.push_front(i) ;
}
for(int i = 1 ; i <= n ; i ++ )cout<<ans[i]<<"\n";
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号