洛谷P1725 琪露诺

洛谷P1725 琪露诺

题目大意：

​ 跳格子，假设当前所在格子是x，每次只能跳到[x+l,x+r]中的一个，跳到一格就能加那一格的冰冻值，问跳出后最高冰冻值是多少。

思路：

​ 打眼一看是一道dp。i位置是由[i - r ,i - l]跳过来的。状态转移方程是：f[i] = max(f[i] , a[i] + f[j]) f属于[i - r,i - l]。所以产生了一个很自然的想法：遍历从l开始到n+r，做动态规划。最后答案在[n,n+r]中找f的最大值 。如下图：

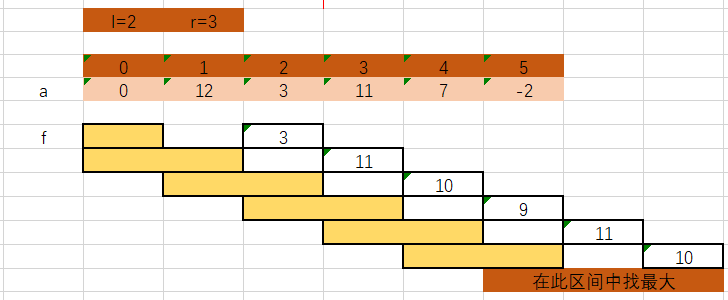
但是会存在一个问题：最大值不一定是从0转移过来的。题目中要求从0开始往右边跳。

​ 于是，在一番苦思冥想之后，我想出了一个蛮巧妙的办法：从后往前跳。因为总有点是跳不到0的，但是我们不用管他，我们最后的答案是f[0] 。

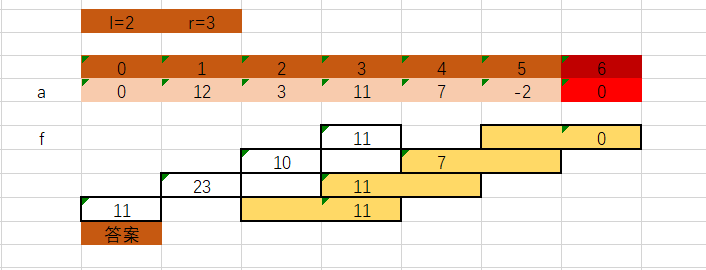
​ 做这个方法的时候，要注意最后在n+1的位置要补r-l个0（代码实现的话，就是dequeue初始压入一个0），至于为什么，可以看以上这个样例，若队列一开始是空的，就会把-2往前转移，而这是不应该发生的。

这是动态规划题，而动态规划的“老三步”是：

1、明确数组定义

2、初始化

3、转移方程

这一题的初始化就是要在n-l到n将f[i]的初值赋成a[i]。然后开始向前转移 。

​ 看到这里有人就要问了，找最大值，那整个方法的复杂度不就成n^2了吗？

但观察上图，这不是单纯的区间最大值，而是滑动区间最大值，那就是可以用到双端队列进行优化：

​ 维护一个单调递减的双端单调队列，每次访问最大值的时候把不在区间内的（不在图中黄色区域的）过滤掉就可以了。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll ;
const ll N = 2 * 1e6 +5000 ;

ll n , ans , l , r ;
ll a[N] , f[N] ; 
deque<ll> q ;

int main(){
	cin>>n>>l>>r ;
	for(ll i = 0 ; i <= n ; i ++ )cin>>a[i] ;
		
	for(ll i = n ; i >= n - l ; i -- )f[i] = a[i] ;
	
	q.push_back(n + 1) ;//初始化，0入队
	
	for(ll i = n ; i >= l ; i -- ){//从i-l跳到[i,i-l+r]
		while(q.size() && f[q.back()] <= f[i])q.pop_back() ;
		q.push_back(i) ;
		while(q.size() && q.front() > i - l + r)q.pop_front() ;
		
		f[i - l] = f[q.front()] + a[i - l] ;
		
	}
	
	cout<<f[0] ;
}