Codeforces Round #738 (Div. 2)
Codeforces Round #738 (Div. 2)
题目大意:
有一个数列,可以选择无限次区间,把区间[l,r]里的第i个数替换成 a[l+i] & a[r-i]
要求这个序列最后可能的最大值里的最小值。
思路:
有关位运算的题目就用二进制来看,有n个数,就把他当成是一个n*k的二维数组,其中k是最大数的二进制位数,本题k取30就可以(a[i]<=1e9)。这种想法在二进制位运算里很常见,可以康一康这个Moamen and XOR。
因为可以执行无数次题中所描述的操作,而我们要找n个数里最大值的最小值,所以对于每一个二进制位,可以变0就尽量变0 。那只要n个数里有一个二进制位i是0,就让它变0就可以了。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int n,m,T;
inline ll read(){
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c)){
ans = ans * 10 + c - '0';
c = getchar();
}return ans;
}
int main(){
T = read();
while(T--){
n = read();
bitset<30> a[200];//bitset是位运算里很常用的
ll b = 1,ans = 0;
for(int i = 1;i <= n; i++){
ll t = read();
a[i] = (t);
}
for(int j = 0;j <= 30; j++){
int f = 1;
for(int i = 1;i <= n; i++)
if(a[i][j] != a[1][j]){
f = 0;break;
}
if(f && a[1][j])ans += b;
b <<= 1;
}
printf("%lld\n",ans);
}
}
写完以上代码a掉后我一想,好像我在做的事情就是把n个数字与起来啊,淦!然后我又打了一个直接全部与起来的,a掉了。不知道应该是什么心情,人麻了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 2*1e8+10;
inline int read(){
int ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c)){
ans = ans * 10 + c - '0';
c = getchar();
}return ans;
}
int T,n,tmp,ans;
int main(){
T = read();
while(T--){
n = read();
ans = read();
for(int i = 2;i <= n; i++){
tmp = read();
ans &= tmp;
}
printf("%d\n",ans);
}
}
===================================================================
题目大意:
有蓝红两种颜色,如果相邻两格是一样的颜色就要加分数,请你再?处涂色,使分数最小。
思路:
分两种情况考虑:
1.开头?,找后面第一个颜色,交替往前涂色。
2.中间?,找前面第一个颜色,交替往后涂色。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 2*1e8+10;
int T;
ll n,m,ans;
inline ll read(){
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c)){
ans = ans * 10 + c - '0';
c = getchar();
}return ans;
}
ll find(string s,char x,ll st){
for(ll i = st;i < s.length(); i++)
if(s[i] == x)return i;
return n;
}
int main(){
T = read();
while(T--){
n = read();
string s;
s.clear();
cin>>s;
ll poschr=1,pos = find(s,'?',0);
while(1){
if(pos == -1)break;
ll B = find(s,'B',pos);
ll R = find(s,'R',pos);
poschr = (B < R)?B:R;
if(poschr == n)break;
if(!pos){
for(int i = poschr-1;i >= 0; i--){
s[i] = (s[i+1] == 'B')?'R':'B';
}
}else{
for(int i = pos;i < poschr ; i++){
s[i] = (s[i-1] == 'B')?'R':'B';
}
}
pos = find(s,'?',poschr+1);
if(pos == n)break;
}
if(poschr == n){//末尾?单独考虑
for(int i = find(s,'?',0);i <= n; i++){
s[i] = (s[i - 1] == 'B')?'R':'B';
}
}
cout<<s<<"\n";
}
}
害,这么简单的题wa了好几次,所以说小数据别想得太多,直接暴力就好。
===================================================================
题目大意:
有n+1个点,前n-1个点都和后一个点相通(1到2,2到3,...,n-2到n-1),然后给n个0或1,0代表i连n+1,1代表n+1连i。问能不能每个点不重复地遍历到一遍。
思路:
首先,分析一下是不会有-1的情况的。全0,全1,首0尾1中间1,首0尾1中间0,都是可以走得通的。所以走通分成了一下两种情况:
case1:
若n+1直接能走到1,不论后面怎么样直接n+1,1,2,3,4,……;
若n能直接走到n+1,直接1,2,3,……,n,n+1。如下图:
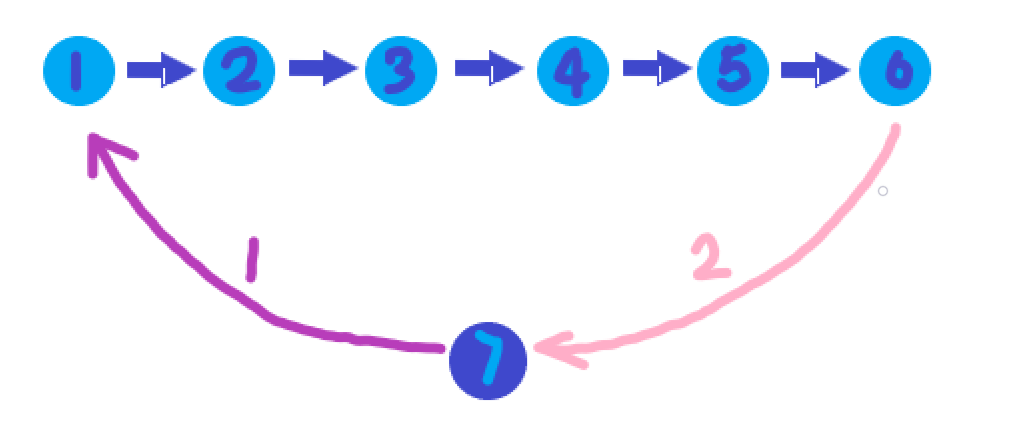
case2:
n+1在中间,要通过某个数x到n+1,再从n+1到x+1 。这种情况体现在输入数据上就是有“01”。如下图:
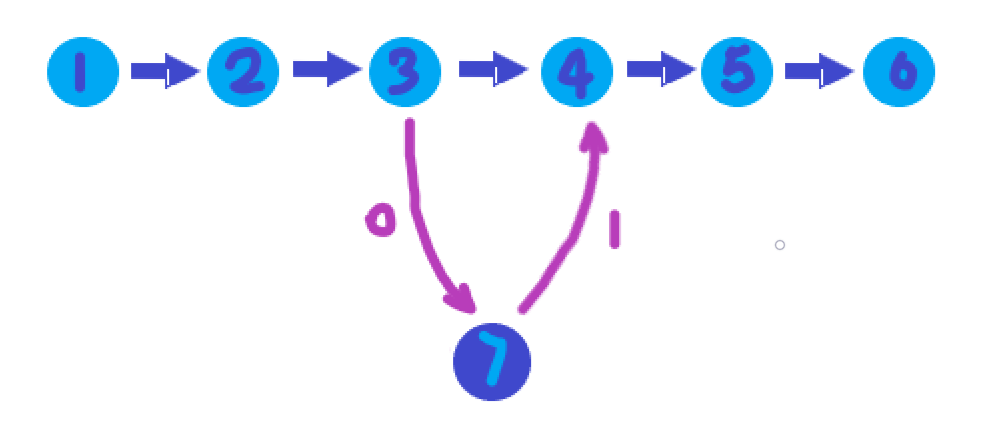
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 1e4+50;
int T,n;
int a[N];
inline ll read(){
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c)){
ans = ans * 10 + c - '0';
c = getchar();
}return ans;
}
int main(){
scanf("%d",&T);
while(T -- ){
scanf("%d",&n);
memset(a,0,sizeof a);
for(int i = 1;i <= n; i++)
scanf("%d",&a[i]);
if(!a[n]){
for(int i = 1;i <= n+1; i++)
printf("%d ",i);printf("\n");
continue;
}
if(a[1]){
printf("%d ",n+1);
for(int i = 1;i <= n; i++)
printf("%d ",i);printf("\n");
continue;
}
int f = 1;
for(int i = 1;i < n; i++){
printf("%d ",i);
if(!a[i] && a[i+1] && f){
printf("%d ",n+1);
f = 0;
}
}printf("%d\n",n);
}
}
D1.Mocha and Diana (Easy Version)
D2.Mocha and Diana (Hard Version)
这两题本质上是一样的,只是数据范围的区别。用o(n)的方法都能解决。
题目大意:
有两个森林,若在两个森林里的对应两点都不在同一颗树上,那么在可以在他们之间加一条边。问最多可以加多少条边。
思路:
将所有在两个森林里的点都和1连起来。这样之后森林1里不和点1连通的就必在森林2里和点1连通 。同理,森林2里不和点1连通的就必在森林1里和点1连通。(这里可以想一想)
最后只要找到两个森林里的“孤儿”连起来就行了。
判断是否相连用一下并查集就行,注意要路径优化。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 1e5+500;
int n,m1,m2,u,v;
int sup[3][N];
vector<pair<int,int> >ans;
inline ll read(){
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c)){
ans = ans * 10 + c - '0';
c = getchar();
}return ans;
}
int find(int x,int num){
return sup[num][x] == x? x : sup[num][x] = find(sup[num][x],num);
}
void join(int x,int y,int num){
int supx = find(x,num);
int supy = find(y,num);
if(supx < supy)sup[num][supy] = supx;
if(supx > supy)sup[num][supx] = supy;
}
int main(){
n = read();
m1 = read();
m2 = read();
for(int i = 1;i <= n; i++)
sup[1][i] = sup[2][i] = i;
for(int i = 1;i <= m1; i++){
u = read();
v = read();
join(u,v,1);
}
for(int i = 1;i <= m2; i++){
u = read();
v = read();
join(u,v,2);
}
for(int i = 2;i <= n; i++){
if(find(i,1) != 1 && find(i,2) != 1){
join(1,i,1);
join(1,i,2);
ans.push_back(make_pair(1,i));
}
}
for(int i = 2,j = 2 ;i <= n; i++){
if(find(i,1) != 1){
while(j <= n && find(j,2) == 1)j++;
if(j > n)break;
join(i,1,1);
join(j,1,2);
ans.push_back(make_pair(i,j));
}
}
printf("%d\n",ans.size());
for(int i = 0;i < ans.size(); i++)
printf("%d %d\n",ans[i].first,ans[i].second);
}
===================================================================
写不动了最后一题下次再更 886




 浙公网安备 33010602011771号
浙公网安备 33010602011771号