SUM-HDU4705

SUM-HDU4704

题目链接：[](Problem - 4704 (hdu.edu.cn))

题目大意：

给定一个n,n<10⁽¹⁰5),求满足
$$
\Sigma s(k) ==n
$$
的数列数量。

思路：

n的范围太大了，o(n)的算法都够呛，可以考虑先打表试着找规律。找不到就别做了。

Step1：

先写个暴力dfs算法试试。

暴力思路：i从0开始到n，若n-i==0，ans++

这个思路还是比较巧妙的8

#include<bits/stdc++.h>
using namespace std;
long long n,ans;

void dfs(int x){
	
	for(int i=1;i<=x;i++)
	if(x>i)dfs(x-i);
	else if(x==i)ans++;
	
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		ans=0;
		dfs(i);
		cout<<"x="<<i<<" "<<"ans="<<ans<<"\n";
	}
} 

以上代码输入n=12，得出的答案如下，很容易能看出ans和x的关系：ans=2**(x-1)

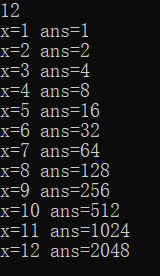
最大的n是10**100000，现在只要解决 2**（10**1e5）%(1e9+7)怎么算就好...

---

Step2:

有欧拉公式和欧拉降幂：

phi(n) =n*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)...

a**(phi(p))%p==1 (a和p互质)

有以上两个公式就可以将式子化简：

p = 1e9+7

2**(10**1e5)%p = 2**((10**1e5)%p)%p

可以看到2的指数为(10**1e5)%p,进入了int范围，就可以算了。

---

Step3：

用string读入，高精度模算出(2**1e5)%p。

高精度模运算就是一个模拟除法的过程。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M = 1e9+7;
const ll fi = 1e9+6;
string s;

ll getp(){
	ll ans=0;
	for(ll i=0;i<s.length();i++){
		ans=(ans*10+s[i]-'0'+fi)%fi;
	}
	return ans;
}

ll fp(ll b,ll p){
	ll ans=1;
	while(p){
		if(p&1)ans=ans*b%M;
		p>>=1;
		b=b*b%M;
	}
	return ans;
}

int main(){
	while(cin>>s){
		cout<<fp(2,getp()-1)<<"\n";
		s.clear();
	}
	
}