一道数学题

【题目】

 P4881 hby与tkw的基情 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

【题目描述】

　

 

 

【输入格式】

　　

【输出格式】

　　

【样例】

【样例输入1】

2
1
3

【样例输出1】

26
2054

【数据范围与提示】

---

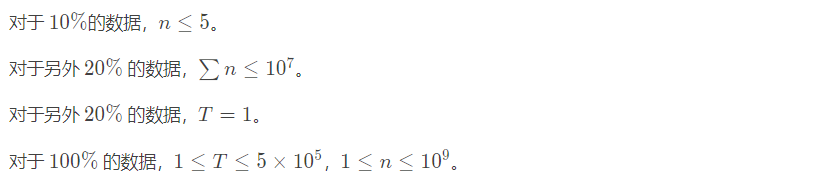
【解题思路】

　　首先，先想到的是暴力做法。

20分代码

#include<cstdio>
using namespace std;
const int MOD = 1e9+7;
const int MAXN = 5000005;
 
int t,n,a[MAXN],last,lm;
  
int main()
{
    scanf("%d",&t);
    int i;
    a[1]=26,a[2]=2054,a[3]=89934;
    last=6,lm=17576;
    while(t--)
    {
        scanf("%d",&n);
        for(i=last+1;i<=n;++i)
        {
            if(i>n) break;
            if(~i&1) continue;
            lm=lm*26%MOD;
            a[(i+1)/2]=(a[i/2]+lm*i%MOD)%MOD;
        }
        printf("%d\n",a[(n+1)/2]);
        last=n;
    }
    return 0;
}

　　

　　明显数据过大，数组存不下，而且会超时。

　　而数据过大就要想压缩中间的运算过程。然后我们就可以发现这是一道数学题。我怎么没有发现（bushi

【正确思路】

　　我们将运算过程浅浅列出来：

• s数组的变化：

  26^1,26^1,26^2,26^2,26^3,26^3......26^(n+1)/2，26^(n+1)/2由于公式中有布尔数组，n为偶数的时候就不会算入答案，我们就列式为：

   

  Ans=1*26^1+(1*26^1+3*26^2)+(1*26^1+3*26^2+5*26^3)+......+(1*26^1+3*26^2+......+n*26^(n+1)/2)
• 这不是高一学的数列求和吗，然后我们就可以用错位相减法来求通项公式：
• 令x=(n+1)/2,Tx为第x项的和
• Tx=1*26^1+3*26^2+5*26^3+......+(2x-1)*26^x
• -25*Tx=2*(26^2+26^3+26^4+......+26^x)+26-(2x-1)*26^(x+1)
• Tx=[(2x-1)*26^(x+1)-x-2*26^2(26^(x-1)-1)/25]/25
• 公式就推导出啦（以上都省略了模数），接着就用代码实现，首先n会很大则26的幂次运算会花费很多时间要引入快速幂，其次是在模1000000007意义下除25，要求逆元，可以在程序里预处理，也可以先求出来直接赋值，这里我直接赋值。

　　AC代码 

#include<cstdio>
using namespace std;
const long long MOD = 1e9+7;
const int MAXN = 5000005;
const long long ni = 280000002; //25在mod1000000007意义下的逆元


long long t,n;

inline long long mi(long long a,long long b,long long p)
{
	long long ans=1;
	while(b)
	{
		if(b&1)
			ans=ans*a%p;
		b=b>>1;
		a=a*a%p;
	}
	return ans;
}//快速幂

int main()
{
	scanf("%lld",&t);
	int i;
	long long ans;
	while(t--)
	{
		scanf("%lld",&n);
		if(n==1||n==2)
		{
			printf("26\n");
			continue;
		}
		n++,n>>=1ll;
		ans=((2*(26*26*(mi(26,n-1,MOD)-1)%MOD*ni%MOD)%MOD)+26)%MOD;
		ans=((n*2-1)*mi(26,n+1,MOD)%MOD-ans+MOD)%MOD;
		ans=(ans*ni%MOD)%MOD;
		printf("%lld\n",ans);
	}
	return 0;
}

　　完结撒花