梯度下降算法(Gradient Descent)：模型训练中最常用的一种算法

梯度下降算法(Gradient Descent)：模型训练中最常用的一种算法
一.算法产生背景

1.穷举法：提前设定好参数的准确值在某个区间并以某个步长进行穷举

穷举法的思想在参数比较多，即维度比较大的情况下会产生唯独诅咒，在一个N维曲面中找一个最低点，使得原问题不可解，基于这样的情况需要进行改进

2.分治法：大化小，小化无，先对整体进行分割采样，在相对最低点进行进一步采样，直到其步长与误差符合条件

两个缺点：a.容易只找到局部最优解，而不易找到全局最优解

                  b.如果需要分的更加细致，则计算量仍巨大

由于存在以上问题，提出了参数优化，即求解使loss最小时的参数的值
二.梯度下降算法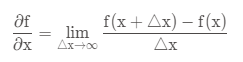

 

 

梯度：梯度即导数变化最大的值，其方向为导数变化最大的方向

如果令\Delta x＞0，则对于增函数，梯度的方向为函数上升的方向，对于减函数，梯度的方向为函数下降的方向。这些方向都不是离极值点渐进的方向，因此需要取梯度下降的方向即梯度的反方向作为变化方向。

梯度下降算法：以凸函数为例，对于当前所选择的w值，显然并不是最低点，而对于将要到达的全局最低点，当前点只能向下取值，即向梯度下降的方向变化。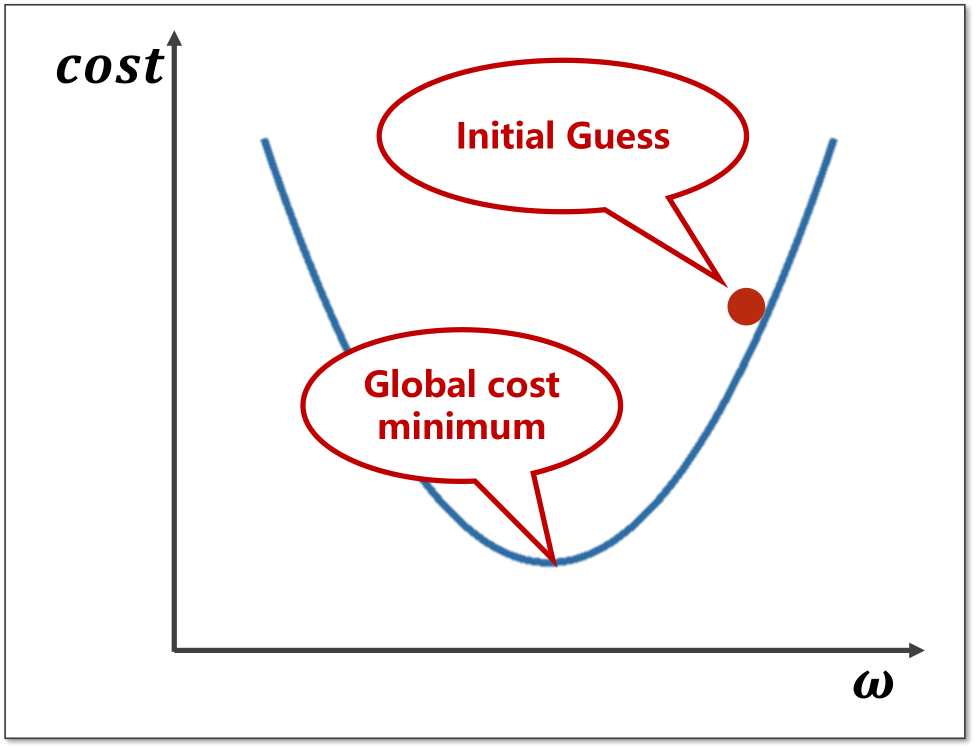

 

 

则取值点需要向下更新，所取的梯度即为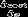，更新的公式为：

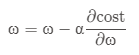
其中α为学习率，即所下降的步长，步长不宜取太大

                                                     

 

 

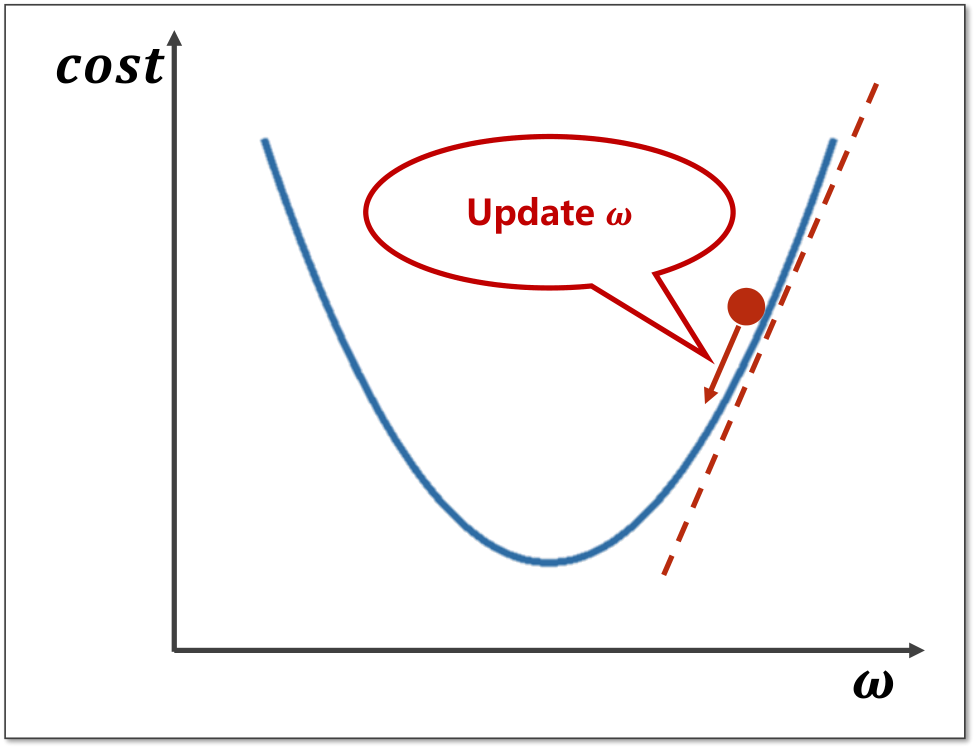
局限性：

a. 梯度下降算法容易进入局部最优解(非凸函数)

b. 梯度下降算法容易进入鞍点

公式：

由上一篇可知：

 

 

 

 

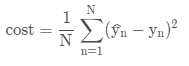
其中：

 

 

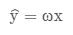
则：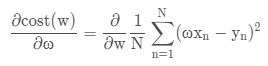

 

 

 

 

 

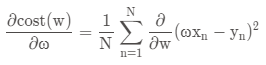
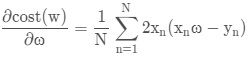
即：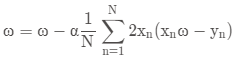

 

 
原文链接：https://blog.csdn.net/jackydyy/article/details/117233000