2025-2026-1 20231301 《信息安全设计》第四周学习总结
2025-2026-1 20231301 《信息安全设计》第四周学习总结
目录
作业信息
| 作业 | 链接 |
|---|---|
| 作业课程 | <班级>(2025-2026-1 信息安全设计) |
| 作业要求 | <作业>(2025-2026-1 信息安全设计 预习作业要求) |
| 作业目标 | 《Head First C 嗨翻C语⾔》 第五章 《Windows C/C++ 加密解密实战》> 预习第六、八、十三、十四章 |
| 作业正文 | <博客>(第四周学习总结) |
学习内容总结
第5章:结构体、联合体和位域
结构体
- 结构体的定义与使用
结构体允许将不同类型的数据组合成一个自定义的复合数据类型,用于表示现实世界中的复杂实体。
cstruct fish {
const char *name; // 字符串指针
const char *species; // 字符串指针
int teeth; // 整型
int age; // 整型
};
- 结构体初始化与访问
// 初始化结构体
struct fish snappy = {"Snappy", "Piranha", 69, 4};
// 访问结构体成员
printf("Name: %s\n", snappy.name);
snappy.teeth = 68; // 修改成员值
- 结构体嵌套
结构体可以包含其他结构体,构建更复杂的数据结构:
cstruct preferences {
struct meal food;
struct exercise exercise;
};
struct fish {
// ...其他成员
struct preferences care;
};
- typedef简化
使用typedef可以创建结构体类型的别名:
ctypedef struct {
const char *name;
int age;
} person;
person p = {"Alice", 25};
联合体
- 联合体的特性
联合体允许在同一内存位置存储不同的数据类型,但同一时间只能存储其中一个成员。
ctypedef union {
short count; // 短整型
float weight; // 浮点数
float volume; // 浮点数
} quantity;
- 联合体初始化方式
quantity q = {4};
// 指定初始化器
quantity q = {.weight=1.5};
// 分步初始化
quantity q;
q.volume = 3.7;
- 联合体与结构体结合
ctypedef struct {
const char *name;
quantity amount;
} fruit_order;
fruit_order apples = {"apples", .amount.weight=4.2};
枚举(Enums)与类型安全
- 枚举的基本用法
枚举用于定义一组命名的整数常量,提高代码可读性:
cenum colors { RED, GREEN, BLUE };
enum colors favorite = BLUE;
- 联合体类型标记
使用枚举标记联合体中当前存储的数据类型:
ctypedef enum { COUNT, POUNDS, PINTS } unit_of_measure;
typedef struct {
quantity amount;
unit_of_measure units;
} order;
位域(Bitfields)
- 位域定义
位域允许指定结构体成员占用的位数,节省内存空间:
ctypedef struct {
unsigned int low_pass_vcf : 1; // 1位存储
unsigned int filter_coupler : 1;
unsigned int reverb : 1;
unsigned int month_no : 4; // 4位存储(0-15)
} synth;
- 位域设计原则
1位字段:存储布尔值(true/false)
3位字段:存储0-7的值
4位字段:存储0-15的值
ctypedef struct {
unsigned int first_visit : 1;
unsigned int come_again : 1;
unsigned int fingers_lost : 4;
unsigned int shark_attack : 1;
unsigned int days_a_week : 3;
} survey;
对比表
| 特性 | 结构体(struct) | 联合体(union) | 位域(bitfield) |
|---|---|---|---|
| 存储方式 | 所有成员独立存储 | 共享同一内存空间 | 精确控制位数 |
| 内存占用 | 各成员大小之和 | 最大成员的大小 | 自定义位数 |
| 用途 | 描述复杂对象 | 存储不同类型数据 | 节省空间存储小范围值 |
| 访问 | 同时访问所有成员 | 同一时间只能访问一个成员 | 按位访问 |
| 示例 | struct | union | struct |
第6章 非对称算法RSA的加解密
1.数学基础
- 素数/质数、互质数、模运算、欧拉函数
- 扩展欧几里得算法(图6-1)
python# 扩展欧几里得算法示例
def extended_gcd(a, b):
if b == 0:
return (a, 1, 0)
else:
g, x, y = extended_gcd(b, a % b)
return (g, y, x - (a // b) * y)
2.RSA算法流程
- 密钥生成:选择大素数p,q → 计算n=pq → 选择e → 计算d ≡ e⁻¹ mod φ(n)
- 加密:c ≡ mᵉ mod n
- 解密:m ≡ cᵈ mod n
3.OpenSSL实战
生成密钥对:
bashopenssl genrsa -out private.key 2048
openssl rsa -in private.key -pubout -out public.key
思维导图
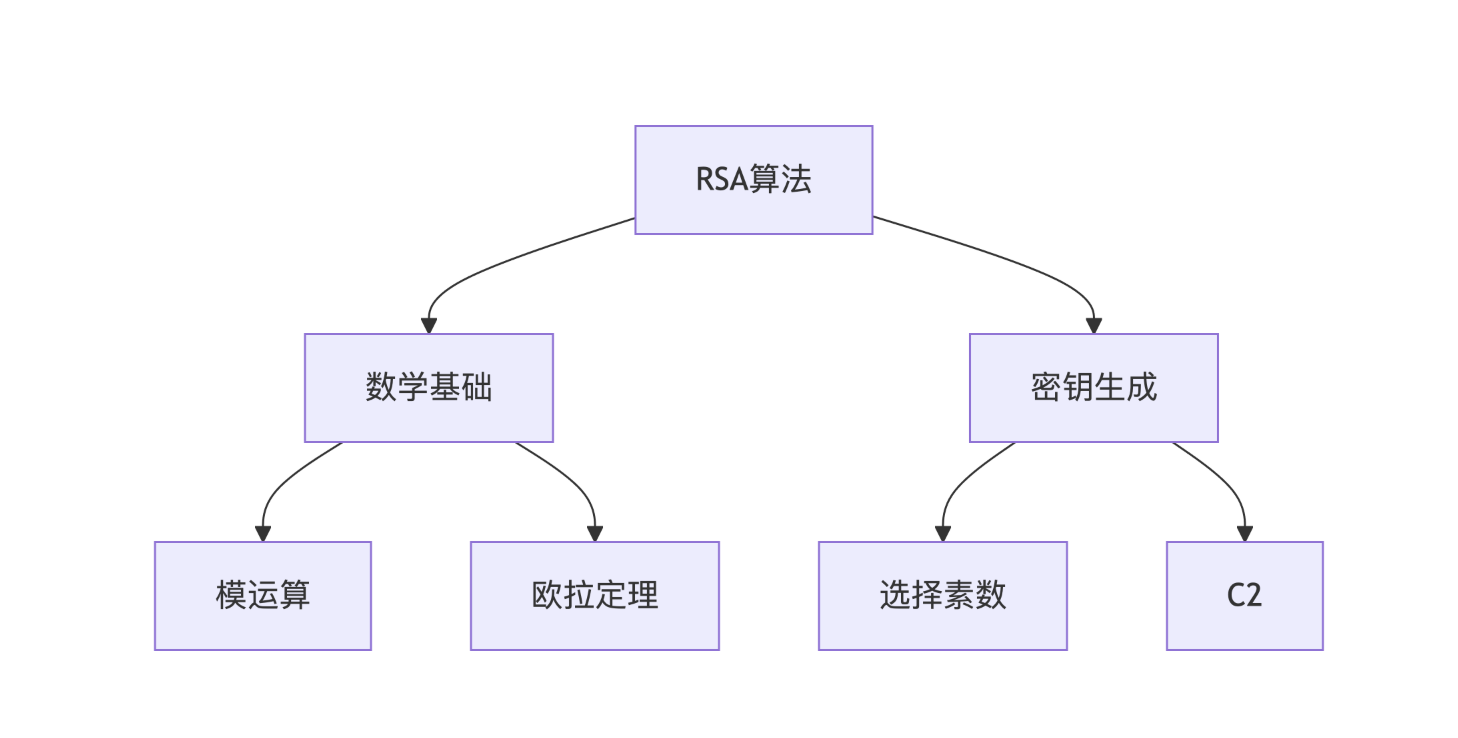
第8章 椭圆曲线密码体制
1.ECC核心概念
- 椭圆曲线方程:y² = x³ + ax + b
- 有限域运算(Fp和F₂ᵐ)
- 点加/倍点运算规则(图8-1)
2.ECC优势
相同安全强度下密钥更短(256位ECC ≈ 3072位RSA)
计算效率更高
3.OpenSSL实现
cEC_KEY *key = EC_KEY_new_by_curve_name(NID_secp256k1);
EC_KEY_generate_key(key);
思维导图
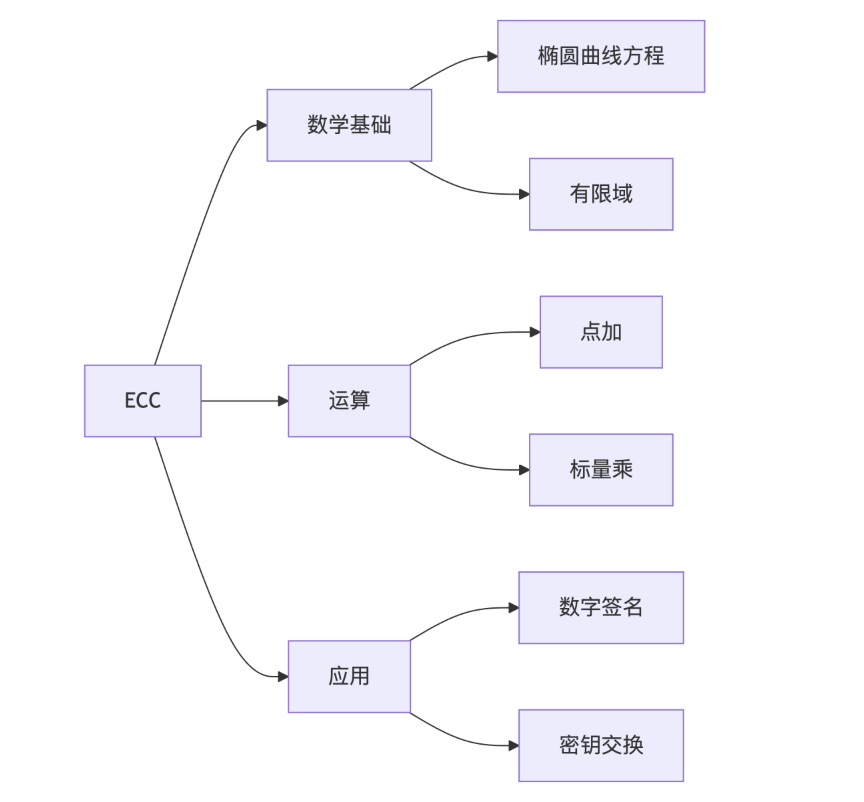
第13章 SM2算法的数学基础
1.素域与二元扩域
素域Fp:y² = x³ + ax + b
二元扩域F₂ᵐ:y² + xy = x³ + ax² + b
2.核心运算
点压缩/解压缩
椭圆曲线离散对数问题(ECDLP)
3.参数验证
判别式Δ = -16(4a³ + 27b²) ≠ 0
基点G的阶验证
思维导图
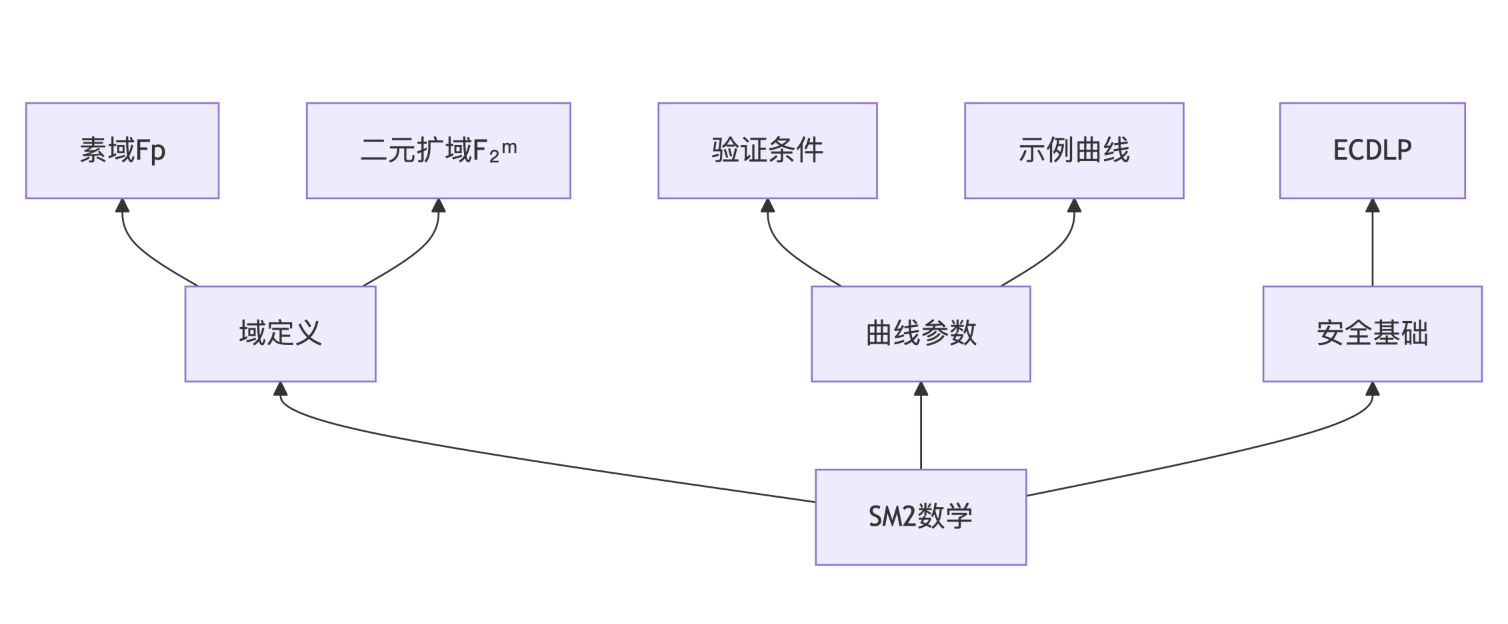
第14章 SM2算法的实现
1.算法参数
推荐曲线:sm2p256v1
哈希算法:SM3
密钥长度:256位
代码实现
// 使用MIRACL库实现
big a,b,p,Gx,Gy,n;
ecurve_init(p,a,b,MR_PROJECTIVE);
epoint *G = epoint_init();
epoint_set(Gx,Gy,0,G);
国密优势:
自主可控
满足《密码行业标准》
思维导图
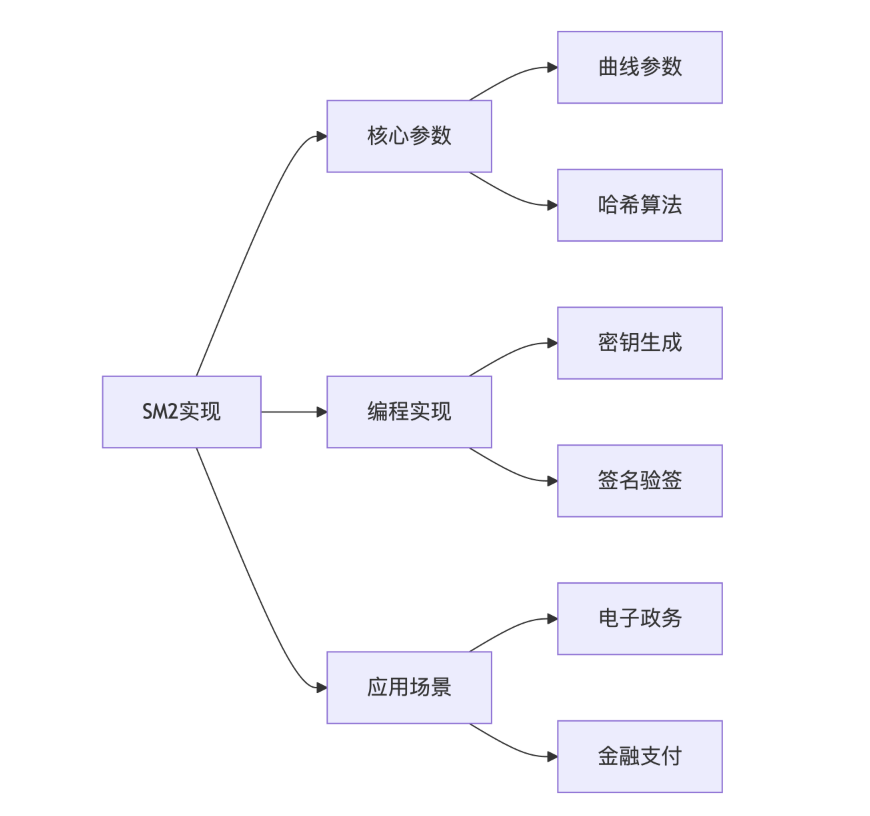
posted on 2025-09-30 10:00 20231301周子昂 阅读(9) 评论(0) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号