2025.03 做题记录

*：瞄了一眼题解就会了

**：看了题解

1. P5283 [十二省联考 2019] 异或粽子 **

首先用处理出前缀异或和，开一个Trie全部存下。对于 \(\text{xor}[l,r]\) ， \(\text{xor}[r,l]\) 是相等的。所以考虑让 \(k\gets 2k\)，这样就不用让 \(l<r\)。

对于 \(w\)，我们可以在 \(O(\log V)\) 求出与 \(w\) 异或后第 \(k\) 大的值。类似线段树二分。

所以对于 \(i\in[0,n]\)，先求出与其最大的异或和，存入堆内。

每一次从堆顶取出元素，如果这是 \(w\) 的第 \(k\) 大值，就计算 \(w\) 的第 \(k+1\) 大值存入堆。这样取 \(2k\) 次的和就是答案。

时间复杂度 \(O(n\log n\log V)\)。

提交记录

2. P4559 [JSOI2018] 列队 *

首先对于区间 \([l,r]\) 的学生，我们将其的位置排序后存入数组 \(a_{l\sim r}\)，一定存在一个 \(x\)，使得 \([a_l,x]\) 的学生都往右跑，\([x,a_r]\) 的学生往左跑。

所以考虑用主席树+二分的方式，设区间 \([a_l,x]\) 有 \(k\) 个学生，则需找到 \(x\le X+k-1\) 最大的 \(x\)。其中 \(X\) 为集合位置。

这样做是 \(O(n\log n\log V)\)，常数很大。只能拿 70pts。

考虑将主席树外二分改为主席树内二分。可以优化到 \(O(n\log n)\)。可以通过。

提交记录

3. P7518 [省选联考 2021 A/B 卷] 宝石

把有向路径 \((u,v)\) 拆成 \((u,lca)\) 和 \((lca,v)\)。

对于每一个点，对它祖先内最近的 前一个宝石和后一个宝石连边，构成两种不同的树。用于倍增。

先由 \(u\) 开始，向上并向后（宝石顺序）倍增。找到 \((u,lca)\) 的填入宝石个数 \(x\)。

再考虑 \((lca,v)\)。如果从 \(lca\) 开始跳很不方便，路径很难被限制。所以考虑从 \(v\) 向上跳。

开一棵主席树记录每一个节点的祖先中各个宝石的最近祖先节点。

然后在主席树上二分，如果从该宝石的最近祖先节点开始，向上并往前跳，是否能跳到宝石顺序 \(\le x\) 的点。

时间复杂度 \(O(n\log m\log n)\)。

提交记录

4. P4587 [FJOI2016] 神秘数 **

首先要先搞懂如何查询答案。

设当前可以表示 \([1,x]\) 的所有数，设下一个没用过的最小的数为 \(u\)。

• 当 \(u\le x+1\)，则可以表示 \([1,x+u]\)。
• 否则不能表示 \(x+1\)。

所以考虑用可持久化值域线段树维护区间的每个数的出现次数。动态维护 \(x\)，如果值在 \([1,x]\) 的数的和 \(sum\) 满足 \(sum>x\)，则让 \(x\gets sum\)。否则输出 \(x+1\)。

根据打表可知每一次 \(x'\ge 2x\)。所以在 \(O(\log V)\) 次就会结束。

时间复杂度 \(O(n\log n+q\log n\log V)\)。

提交记录

5. P6071 『MdOI R1』Treequery *

首先，需要维护出 \(\operatorname{lca}[l,r]\)。用线段树维护。这里求LCA考虑用ST表+欧拉序列维护，以减小时间复杂度。

现在考虑 \((root,p)\) 这条路径。\(\operatorname{lca}[l,r]\) 以下简记为 \(lca\)。

进行分类讨论：

• 如果 \(lca\) 在 \(p\) 的子树内，则答案为 \(dis(lca,p)\)。

• 如果 \(lca\) 不在 \(p\) 的子树内 且 \(p\) 的子树内有 \([l,r]\) 的点，则答案为 \(0\)。

• 如果 \(lca\) 不在 \((p,root)\) 路径上，则答案为 \(dis(p,lca)\)。

  判定办法：如果 \(\operatorname{lca}(lca,p)\neq lca\)，则 \(lca\) 不在 \((p,root)\) 路径上。

• 否则，则需找到 \((p,root)\) 上最深的点 \(x\) 使得该点的子树内有 \([l,r]\) 的点。

  这个 \(x\) 可以用 主席树+倍增 找到。则答案为 \(dis(x,p)\)

那么如何判定 \(p\) 内是否有 \([l,r]\) 的点？

如果用启发式合并+主席树，需要 \(O(n\log ^2n)\) 的时空复杂度。但是如果用dfs序，就只用 \(O(n\log n)\) 的时空复杂度。

所以总时间复杂度 \(O(n\log n+q\log ^2n)\)。

提交记录

6. P3567 [POI 2014] KUR-Couriers *

这么简单的题怎么没想到呢？

可持久化值域线段树维护区间数的出现次数。

然后进行递归处理。如果左子树的出现总数 \(\ge \frac{r-l+1}2\) 就递归左子树，否则递归右子树。

只会递归一个子树，所以时间复杂度是对的。

时间复杂度 \(O(n\log n+q\log n)\)。

提交记录

7. P5795 [THUSC 2015] 异或运算 *

怎么把 可持久化01Trie+二分 转化为 可持久化01Trie内二分 这么简单的优化方法都想不到呢？

首先发现 \(m\le 3\times 10^5\)，但是 \(n\le 1000,q\le 500\)。

感觉时间复杂度是个 \(O(nq\log V(\log V))\) 啥的玩意儿。

于是对 \(b\) 数组建一棵可持久化01Trie。然后对于每一次询问，去二分最终答案，然后枚举 \(a_i\) 去计算 \(b_j\ \text{xor}\ a_i\ge ans,j\in[l,r]\) 的个数。

然后就是 \(O(nq\log^2 V)\)。在可持久化01Trie的常数加持下，我们成功获得 TLE 10pts 的好成绩。

怎么优化？转为可持久化01Trie内二分呗。维护 \(d-u+1\) 个指针，判断答案这一位如果为 \(1\) 时的个数是否 \(\ge k\)，如果满足则为 \(1\)，所有指针同时跳 \(1\)。否则为 \(0\)，所有指针同时跳 \(0\)。

时间复杂度 \(O(m\log m+nq\log V)\)。

提交记录

8. 【0306 B组】 D. 种植 **

题目链接

题意：

一个 \(n\times m\) 的网格。网格上有障碍，有障碍的地方不能通过。现在要从 \((1,1)\) 走到 \((n,m)\)，每一次只能向下或向右走一个。

你需要在网格中选一些不是障碍的点，使得任意一条从 \((1,1)\) 到 \((n,m)\) 的路径上恰好有一个点被选中。求方案数，对 \(10^9+7\) 取模。

\(n,m\le 5000\)。

本质上是一个割的问题，割掉点使得 \((1,1)\) 与 \((n,m)\) 不连通。

先将所有不能到达 \((n,m)\) 或者由 \((1,1)\) 不可达的点抛开不看，因为他们是否被选中不重要。设有 \(x\) 个这样的点，则方案数需 \(\times 2^{x}\)。

现在有一个条件，就是每条路径恰好有一个点被选中。翻译一下，就是被选中的点之间互相不可达。

所以考虑平面图转对偶图，参考平面图最小割转对偶图最短路。

对于一条点，如果我们把它割掉了，就相当于将他的出边都给割掉了。那么我们会建出一个图来。

现在有以下样例：

输入：

5 8
......##
.##..#..
...#....
.....##.
#.......

输出：

432

我们把障碍与 \(3\) 个不可达的点给删去，就得到以下的图：

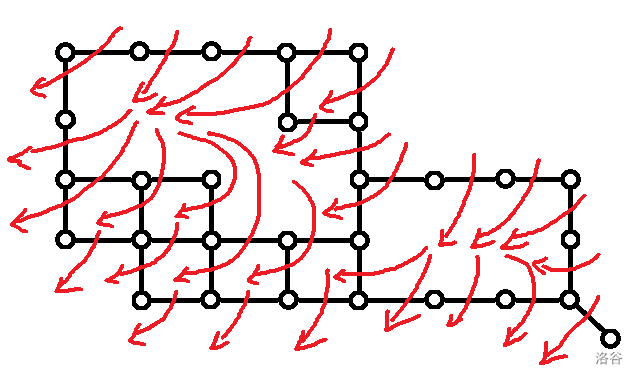
一个空白的格子为一个点。

因为 \((n,m)\) 也可以割掉的，所以还需加一条边。

那么方案数就是从右上走到左下的方案数。也就是图中 \(2^3\times (6\times 6+4\times 4+2)=432\)。

直接模拟即可。时间复杂度 \(O(nm)\)。

提交记录

9. P5298 [PKUWC2018] Minimax *

这个题感觉很线段树合并啊。因为 \(n\le 3\times 10^5\)，而且每一个叶子的值都不相等。

所以直接对于叶子的值离散化，然后考虑用值域线段树存下来。对每一个儿子用动态开点值域线段树存下。

线段树 \(u\) 中下标为 \(i\) 的位置存的是节点 \(u\) 权值为 \(i\) 的概率，记为 \(p_{u,i}\)。同时我们还要维护概率的区间和。

因为保证儿子个数不超过 \(2\) 个，所以当只有一个儿子时，就可以直接继承。否则就需要合并两个儿子的线段树。

如何合并呢？为了保证时间复杂度，我们需要对每一个线段树上每一个节点进行合并。

我们考虑对于节点 \(u\) 的儿子 \(x,y\) 线段树的区间 \([l,r]\) 进行合并。

设 \(xpre=\sum_{i=1}^{l-1} p_{x,i}，xsuf=\sum_{i=r+1}^{n} p_{x,i}，ypre=\sum_{i=1}^{l-1} p_{y,i}，ysuf=\sum_{i=r+1}^{n} p_{y,i}\)。

同时设 \(xsum=\sum_{i=l}^r p_{x,i}，ysum=\sum_{i=l}^r p_{y,i}\)。

则有：

\[\sum_{i=l}^r p_{\text{merge(x,y),i}}=(xsum\times ysum)+(1-p_u)(ysuf\times xsum+xsuf\times ysum)+p_u(xpre\times ysum+ypre\times xsum) \]

其它的都好说，就是关于 \(xpre,xsuf,ypre,ysuf\) 怎么求？如果用 \(O(\log n)\) 查询，那么在动开线段树的加持下肯定TLE。

其实我们可以在往下递归时顺带求出来。就如在递归左子树时，就让 \(xsuf\gets xsuf+右子树 xsum，ysuf\gets ysuf+右子树 ysum\)。

那么就可以直接求出来了。

但是还有一个问题。正常来说，合并 \(x,y\) ，当其中 \(y\) （\(x\) 同理）为空时，正常来说应该直接返回\(x\)。但是此题 \(x\) 的子孙的值应该被更改。因此此处不能直接返回 \(x\)。

那该怎么办？直接递归下去会导致时间复杂度假了，变成 \(O(n^2)\)，我们如何使得可以不用递归下去？

我们先来研究一下这些应该被更改的点会被更改成什么。因为 \(y\) 节点是空节点。所以 \(ysum=0\)。

那么此时

\[\sum_{i=l}^r p_{\text{merge(x,y),i}}=(xsum\times ysum)+(1-p_u)(ysuf\times xsum+xsuf\times ysum)+p_u(xpre\times ysum+ypre\times xsum) \\=(1-p_u)(ysuf\times xsum)+p_u(ypre\times xsum) \\= xsum\times ((1-p_u)\times ysuf+p_u\times ypre)\]

发现其实是同时乘上了一个数。所以可以直接打lazy tag。打一个乘法懒标记就行了。

所以对于 \(x,y\) 中有一个是空节点的情况，直接在另一个节点上打一个乘法懒标记即可。

时间复杂度 \(O(n\log n)\)。

提交记录

10. P4284 [SHOI2014] 概率充电器

考虑期望的线性性。对于元件 \(i\)，设其通电的概率为 \(p_i\)，则答案为 \(\sum_{i=1}^n p_i\times 1=\sum_{i=1}^n p_i\)。=

先考虑 \(O(n^2)\) 做法。

对于一个点，我们设其为树根。然后尝试一下跑dp。

\(dp_{u}\) 表示 \(u\) 不通电的概率，则有转移：

\[dp_{u}=(1-q_u)\prod_{v\in son_u}[1-P(u,v)+P(u,v)dp_v] \]

则 \(i\) 的答案需要以 \(i\) 为根跑一遍dp，让 \(ans\gets ans+dp_{i}\)。

然后就可以 \(O(n^2)\) 进行dp了。

如何优化到 \(O(n)\)？

考虑用换根dp进行加速。通过 \(f_u\) 推出 \(f_v\)。

你会发现，因为 \(dp_u\) 是若干个值乘起来，所以撤销/更改就会比较方便。

因为 \(dp_u=(1-q_u)\prod_{v\in son_u}[1-P(u,v)+P(u,v)dp_v]\)，更改后 \(v\) 不再是 \(u\) 的儿子，所以需要让 \(dp_u\gets dp_u\times [1-P(u,v)+P(u,v)dp_v]^{-1}\)。

同时，\(u\) 会成为 \(v\) 的新儿子，所以让 \(dp_v\gets dp_v\times [1-P(u,v)+P(u,v)dp_u]\) 即可。

但是 \([1-P(u,v)+P(u,v)dp_v]\) 可能会等于 \(0\)，此时让 \(dp_{u}=1\) 即可。

提交记录

11. P10764 [BalticOI 2024] Wall **

设 \(p_i=\max_{j=1}^i h_j，s_i=\max_{j=i}^n h_j\)。

所以答案就是 \(\sum_{i=1}^n \min(p_i,s_i)-h_i\)。

因为 \(p_i,s_i\) 都跟 \(\max\) 有关，而式子里却有 \(\min\)，所以转化一下：

\[\sum_{i=1}^n \min(p_i,s_i)=\sum_{i=1}^n p_i+s_i-\max(p_i,s_i)-h_i\\=-n\times p_n+\sum_{i=1}^n p_i+\sum_{i=1}^ns_i-\sum_{i=1}^nh_i \]

这里面 \(\sum_{i=1}^n h_i=2^{n-1}(a_i+b_i)\)。

接下来就要求 \(\sum_{i=1}^n p_i\) 。

考虑设 \((i,j,h_i)\) 为 \(p_j=h_i\) 的权值和。因为可能出现 \(p_j=h_i\) 的 \(i\) 有多个的情况，所以我们钦定为最小的那个 \(i\) 为最大值所在位置，也就是只计算最小的 \(i\) 与 \(j\) 的在 \(h_i\) 的贡献。

首先先把式子列出来：

\[(i,j,h_i)=h_i\times \prod_{k=1}^{i-1}([a_k<h_i]+[b_k<h_i])\times \prod_{k=i+1}^j ([a_k\le h_i]+[b_k\le h_i])\times 2^{n-j} \]

可以暴力求，就有 \(O(n^2)\) 。

如何优化？

考虑对于一个 \(i\)，将所有 \(j\) 一起处理。为了方便，我们设 \(w(i,h_i)=\prod_{k=1}^{i-1} ([a_k< h_i]+[b_k< h_i])\)。 \(w(i,h_i)\) 可以通过从小到大加入 \(a_i,b_i\)，用单点修改、区间乘积线段树预处理出。

所以有：

\[(i,h_i)=h_i\times w(i,h_i)\times \sum_{j=i}^n 2^{n-j} \prod_{k=i+1}^{j}([a_k\le h_i]+[b_k\le h_i]) \]

此时我们维护 \(f(j,h_i)=\sum_{i=1}^j 2^{n-j} \prod_{k=1}^{j}([a_k\le h_i]+[b_k\le h_i])\)，则有：

\[(i,h_i)=h_i\times w(i,h_i)\times f(n,h_i)\times f(i,h_i)^{-1} \]

而 \(f(j,h_i)\) 相当于对于每一个位置，有一个 \(2^{n-j}\) 的权值，然后求权值乘上一个前缀乘积之和。可以用线段树维护。

所以综上，二者都可以用线段树求得。时间复杂度 \(O(n\log n)\)。

然后 \(\sum_{i=1}^n s_i\) 可以通过左右翻转 \(a,b\) 序列，再跑一遍上述算法得到。

然后 \(p_n=\sum_{i=1}^n (i,n,h_i)\)，可以在上述算法中顺便求出。

时间复杂度 \(O(n\log n)\)。

提交记录

12. CF2077C Binary Subsequence Value Sum

告诫后人：*2300 的题我做了2h，原因是把子序列看成子段了！！！而且考试的时候也看错了，不长记性！！！

\(F(v)\) 本质上是求该序列 \(1\) 的个数 \(-\) 该序列 \(0\) 的个数。

现在我们要将 \(v\) 分成两个部分，然后将 \(F\) 值乘起来。我们发现，当往一个序列后面加入一个数字时，它的 \(F\) 会 \(+1\) 或 \(-1\)。所以对于我们 \(v\) 一定可以拆出一个部分的 \(F\) 值在 \([0,F(v)]\) 之间。

所以

• 当 \(|v|\) 为偶数时，一定可以将 \(F(v)\) 拆成 \(\frac{F(v)}2+ \frac{F(v)}2\)

  此时 \(v\) 的价值为 \(\frac{F(v)}2\times \frac{F(v)}2\)；

• 而当 \(|v|\) 为奇数时，一定可以将 \(F(v)\) 拆成 \(\frac{F(v)+1}2+ \frac{F(v)-1}2=\frac{[F(v)]^2}4\)

  此时 \(v\) 的价值为 \(\frac{F(v)+1}2\times \frac{F(v)-1}2=\frac{[F(v)]^2-1}4\)；

为了让两式一样，我们将 \(\frac 14\) 提出来，然后将 \(|v|\) 为奇数时分子的 \(-1\) 给提出来单独计算，也就是长度为奇数的子序列的个数，即 \(\sum_{i=0}^{\lfloor\frac{n-1}2\rfloor} c_n^{2i+1}\)。

现在问题就转化为对所有子序列 \(v\) ，求 \([F(v)]^2\)。

所以我们设 \(c0\) 和 \(c1\) 为整个序列 \(0\) 的个数和 \(1\) 的个数。

则有

\[\sum_{v}[F(v)]^2=\sum_{i=0}^{c0}\sum_{j=0}^{c1}C_{c0}^iC_{c1}^j(i-j)^2 \\= \sum_{i=0}^{c0}C_{c0}^ii^2+\sum_{j=0}^{c1}C_{c1}^jj^2-2\sum_{i=0}^{c0}\sum_{j=0}^{c1}C_{c0}^iC_{c1}^jij \]

设 \(w_n=\sum_{i=0}^nC_n^ii^2\)。

则有转移 \(w_i=2w_{i-1}+i\times 2^{i-1}\)。

于是式子就是

\[\sum_{v}[F(v)]^2= w_{c0}+w_{c1}-2\sum_{i=0}^{c0}C_{c0}^ii\sum_{j=0}^{c1}C_{c1}^jj \\= w_{c0}+w_{c1}-2\times 2^{c0-1}\times c0\times 2^{c1-1}\times c1 \\= w_{c0}+w_{c1}-2^{n-1}\times c0\times c1 \]

于是每一次修改，只要知道 \(c0\) 和 \(c1\) 就可以 \(O(1)\) 求解。

设 \(l=\sum_{i=0}^{\lfloor\frac{n-1}2\rfloor} c_n^{2i+1}\)。所以答案就是

\[\frac14( w_{c0}+w_{c1}-2^{n-1}\times c0\times c1-l)\]

时间复杂度 \(O(n+q)\)。

提交记录