2024.09 2024.10做题记录

1. CF1925D Good Trip

这题虽然是我自己做出来的，但我真没觉得它只有*1900。

根据期望的线性，则最终答案为各对朋友的期望贡献之和。

对于每一对朋友，\(u\)和\(v\)并不重要，都是等概率事件。

枚举每一对朋友的出现次数\(l\)，则它的贡献是一定的，权值是一个等差数列的和，为\((2w+l-1)\times l\div 2\)。我们设\(d\)为所有可能抽到的一对小同学的情况数，则\(d=\frac{n\times(n-1)}{2}\)，则这对朋友出现的概率为\(\frac{C_{k}^{l}\times (d-1)^{k-l}}{2\times d^k}\)（用组合数求出它可能出现的位置，剩下的都是其它的一对小同学再除以总方案数）。

不难写出答案为 \(\sum_{i=1}^{m}\sum_{l=1}^{k}(\frac{C_{k}^{l}\times (d-1)^{k-l}\times (2w+l-1)\times l}{2\times d^k})\)。

然后直接求是\(O(n^2)\)，过不了，考虑预处理。

发现对于不同的朋友，只有\(w\)会变，所以把式子拆成\(\sum_{i=1}^{m}(w\times \sum_{l=1}^{k}\frac{C_{k}^{l}\times (d-1)^{k-l}\times l}{d^k}+\sum_{l=1}^{k}\frac{C_{k}^{l}\times (d-1)^{k-l}\times (l-1)\times l}{2\times d^k})\)，然后后面这两个带\(\sum\)的式子都可以预处理。

时间复杂度\(O(k\log V+m)\)，实现的好可以到\(O(k+m)\)。

提交记录

2. P3935 Calculating

\(f(x)\)实际上就是 \(x\)的因数个数。

所\(\sum_{i=1}^{x} f(x)=\sum_{i=1}^{x}\lfloor \frac{x}{i}\rfloor\)，用数论分块做，答案为\(f(r)-f(l-1)\)。

时间复杂度\(O(\sqrt V)\)。

提交记录

3. P2260 模积和

这个式子可以转化一下：

\[\sum_{i=1}^{n} \sum_{j=1}^{m} (n \bmod i) \times (m \bmod j), i \neq j\\=(\sum_{i=1}^{n}(n \bmod i) )\times (\sum_{j=1}^{m} (m \bmod j)), i \neq j\\=(\sum_{i=1}^{n}(n \bmod i) )\times (\sum_{j=1}^{m} (m \bmod j))-\sum_{i=1}^{\min(n,m)}(n\bmod i)\times (m\bmod i) \]

前者可以用数论分块求出，但是如何求后者？

后者可以进行进一步转化：

\[\sum_{i=1}^{\min(n,m)}(n\bmod i)\times (m\bmod i)\\=\sum_{i=1}^{\min(n,m)}n\times m-i\times\lfloor\frac{n}{i}\rfloor\times m-i\times\lfloor\frac{m}{i}\rfloor\times n+i^2\times\lfloor\frac{n}{i}\rfloor\times \lfloor\frac{m}{i}\rfloor\\=n\times m\times\min(n,m)+(\sum_{i=1}^{\min(n,m)}-i\times\lfloor\frac{n}{i}\rfloor\times m-i\times\lfloor\frac{m}{i}\rfloor\times n+i^2\times\lfloor\frac{n}{i}\rfloor\times \lfloor\frac{m}{i}\rfloor) \]

数论分块本质上是快速求出最大的\([l,r]\)需满足 \(\lfloor\frac{n}{l}\rfloor=\lfloor\frac{n}{r}\rfloor\) ，而这里需要同时满足\(\lfloor\frac{n}{l}\rfloor=\lfloor\frac{n}{r}\rfloor\)和\(\lfloor\frac{m}{l}\rfloor=\lfloor\frac{m}{r}\rfloor\)，所以每一次r跳的时候，先跳\(\min(\lfloor\frac{m}{\lfloor\frac{m}{l}\rfloor}\rfloor,\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor)\)，再跳\(\max(\lfloor\frac{m}{\lfloor\frac{m}{l}\rfloor}\rfloor,\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor)\)，以保证相等。

时间复杂度 \(O(\sqrt V)\)。

提交记录

4. P4139 上帝与集合的正确用法

求\(2^{2^{2^{2^{...}}}}\bmod p\)，固有\(2^{2^{2^{2^{...}}}}>\varphi(p)\)，设\(b=2^{2^{2^{2^{...}}}}\)，根据扩展欧拉定理有\(2^b\equiv 2^{b\bmod \varphi(p)+\varphi(p)}(\bmod \ p)\)。

而当 \(\varphi(p)=1\)时又有 \(2^b\equiv 2(\bmod \ p)\)，所以考虑递归下去，则有 $2^{2b}\equiv 2^{2b\bmod \varphi(p)+\varphi(p)}(\bmod\ p) $，而 \(2^b\bmod \varphi(p)\)从递归中算出，递归出口为$ 当\varphi(p)=1时，返回2$。

\(\varphi\) 函数用线性筛预处理出。

因为每一次会让 \(p\to \varphi(p)\)，那么这个时间复杂度是多少呢？

会发现有\(\varphi(n)=n\times \Pi\frac{p_i-1}{p_i}\)。

1. 当 $ n $ 为偶数时，一定存在 $ p_i=2 $ ，则 \(\varphi(n)\le \frac{n}{2}\)。
2. 当 \(n\) 为奇数时，若 $ n $ 为质数，则 $ \varphi(n) $ 为偶数，否则则一定存在至少 $ 1 $ 个质因子，所以\(\varphi(n)\le \frac{n}{p}\)。

所以这东西一定是 $ \log $ 级别的。

时间复杂度 \(O(V+T\log^2 V)\)。

提交记录

5. CF1957F1/F2 Frequency Mismatch

这题看起来十分迷糊。

发现 \(k\) 很小，可以考虑值域线段树，然后线段树二分判断两棵线段树该区间内是否有出现次数不一样的值。如果有就往下递归，否则跳过。

如何判断出现次数相同？考虑哈希，需要满足可减性，所以用和哈希，对每一种颜色赋一个随机值，则该区间的值为所有颜色出现次数乘上他的随机值。如果该区间的值不同，就往下递归。

然后怎么得出这条路径上的值域线段树呢？如果用树剖就太难弄了，所以考虑主席树。

哈希写自然溢出吧。

时间复杂度\(O(n\log n+(q+\sum k)\log n)\)。

提交记录

7. CF1982F Sorting Problem Again

我写了几个\(O(q\log^2 n)\)的算法，然后被卡了。。。

考虑怎么搞到\(O(q\log n)\)。

其实用线段树维护出该区间的最长不降前、后缀。如果都为\(n\)则输出-1 -1。否则分别设为\(l,r\)，则区间\([l,n-r+1]\)必须被重排。

但肯定不止这个区间被重排。如\(\{1,4,5,2,3,1,5,6,7\}\)，那么有\(l=3,r=4\)，区间\([3,6]\)被重排，后变成\(\{1,4,1,2,3,5,5,6,7\}\)。但你会发现该结果并不是有序的。我们让\(a_2\)也跟着重排才行。

具体而言，设\(maxn=\max_{i=l}^{r-n+1} a_i,minn=\min_{i=1}^{r-n+1}a_i\)，则所有\(minn \le a_i\le maxn\)的数可能会被重排。

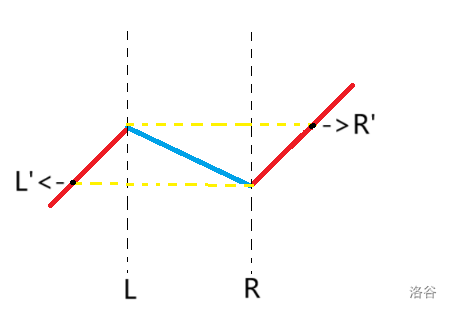
因为\([1,l-1],[n-r+2,n]\)是单调不降的。所以可以直接二分查找。

但是有些数可能不会被重排。就如刚才那个序列，\(minn=1\)，虽然\(a_1\ge minn\)，但无论是否将\(a_1\)加入重排的区间，最终得到的序列都为\(\{1,1,2,3,4,5,5,6,7\}\)，而我们想让重排的区间尽可能小，所以就不把\(a_1\)加入重排区间，这样更优。

所以二分时，找到 \([1,l-1]\) 中第一个大于 \(minn\) 的数和 \([n-r+2,n]\) 中最后一个小于 \(maxn\) 的数即可。

时间复杂度\(O(n+q\log n)\)。

提交记录

8. AT_arc103_d Distance Sums

构造题。

可以发现\(d\)最大的点一定是叶子且\(d\)最小的点一定是重心。

考虑\(u\to v\)时\(d\)值的变化，记\(sz_u\)为删去\((u,v)\)后\(u\)所在连通块的大小，\(sz_v\)同理。

所以有\(d_v=d_u+sz_u-sz_v\)，因为\(sz_v+sz_u=n\)，所以\(d_v=d_u+2\times sz_u-n\)。所以当\(sz_u\)一定时，\(d_v\)一定。所以说我们从叶子向根节点构造树时，当这棵子树一定时，它的父亲节点是一定的。

所以从叶子开始构造。设\(to_u\)为\(u\)节点现在对应的父亲节点的值。而发现\(to_{重心}<to_u\)，所以不妨设重心为根。

开一个大根堆，初始存入所有节点。对于每一个节点，根据当前的子树大小，推算出它的父亲节点的值，然后判断是否有这个值对应的点，如果有就连边，否则判无解。

因为重心为根，所以以根为起点的一条链上的\(d\)值一定时单调递增的，我们通过这个节点找出的父亲节点一定还在堆内。所以当我们用一个节点去找他的父亲节点时，以它为根的这棵子树形态已定，所以直接找。

最后把所有边输出。

但是发现过不了。

最后建成的树可能不连通或不合法，所以要跑一边换根dp验证。

时间复杂度\(O(n\log n)\)

提交记录