P4768 [NOI2018] 归程 题解

题目传送门

前置知识

1. Kruskal重构树

2. 单源最短路Dijkstra $ + $ 堆优化

3. 倍增

题意

一个 \(n\) 个节点、\(m\) 条边的无向连通图（节点的编号从 \(1\) 至 \(n\)）。我们依次用 \(l,a\) 描述一条边的长度、海拔。

我们用水位线来描述降雨的程度，它的意义是：所有海拔不超过水位线的边都是有积水的。

终点在 \(1\) 号节点。接下来 \(Q\) 个询问，每一个询问会告诉你出发点 \(v\) ，以及当天的水位线 $p $ 。

每一次询问在起点处出发时可以沿着任意多条没有积水的边走，并不计算长度。并可以选择在任意时候切换状态，可以走任意边，但是需要加上这条边的长度。切换状态后不能再切换回来。你需要让长度和最小化。

询问之间互相独立，有些测试点强制在线，单个测试点包含 $ t $ 组数据。

思路

我们需要选一个点，使得这个点到一号节点的距离最小且从起点到这个点存在一条路，这条路上的所有边的第二个权值都大于 $ p $ 。

暴力的做法就是搜索出每一个从起点坐车（就是没有切换状态）能到达的所有节点，再对这些点到一号节点的最小距离的和求最小值。

后者可以通过单源最短路解决，通过建反向图（其实不用建，本来就是无向图），从一号节点跑一遍单源最短路，这样到所有点的最短路就等价于这个点到一号节点的最短路。

这里建议使用 Dijkstra $ + $ 堆优化，时间复杂度较为稳定，为 $ O(m\log n) $ 。用spfa会被卡，它死了。

但这样肯定不可能过的，不然怎么是NOI的题呢 ，这样暴力地做时间复杂度最坏为 $ O(t(m\log n+Qn)) $ 。

接下来就是怎么去快速地求起点坐车能到达的点到一号节点距离的最小值了。

这里需要引入一个新的知识点——Kruskal重构树。

具体来说就是有一个无向连通图，在上面用Kruskal跑一遍最小生成树，这颗树有 $ n $ 个节点。但我们想把这棵树扩展一下，让它变成一颗有 $ 2\times n-1 $ 个节点的树，把它用并查集合并的过程用树表示出来。

举个例子，我们有一个无向带权连通图（从日报上抠的图）。

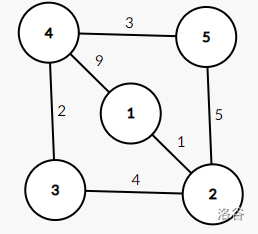
而这是它的最小生成树。

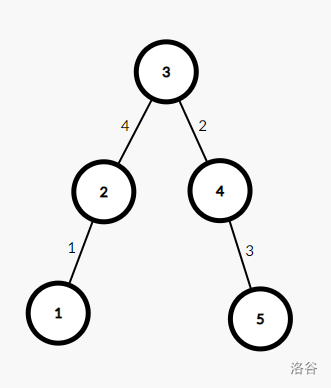
再模拟一下跑最小生成树的过程。先把所有的边从小到大排一个序，再一条一条地加进去。

每加一次就重新创一个点，并连向这条边通向地两个点的 $ fa $ 值，并把这两个点的 $ fa $ 值更新为这个新创建的节点，把这个新创建的点的点权赋值为这条边的边权。

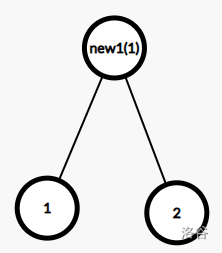
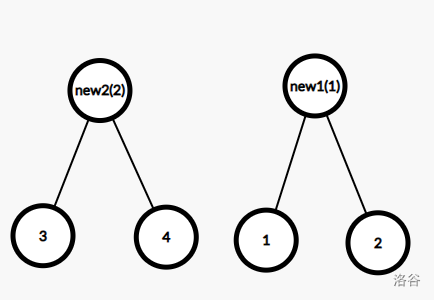
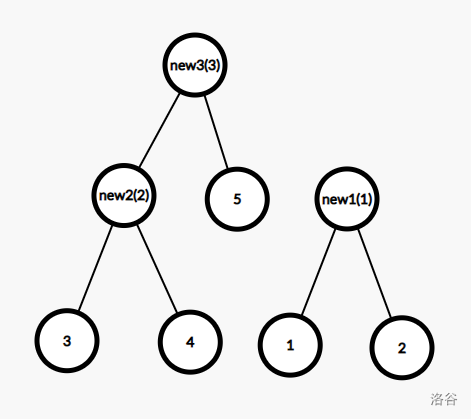
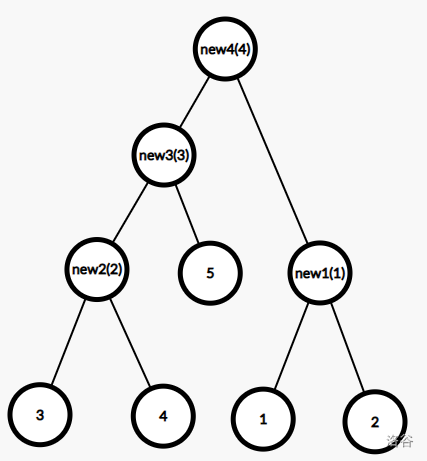
最后我们会得到一个有 $ 2\times n-1 $ 个节点的二叉树。

这颗树有几个性质：

1. 是一棵二叉树。

2. 如果是按最小生成树建立的话是一个大根堆。

3. 主要性质：原图中两个点间所有路径上的边最大权值的最小值 $ = $ 最小生成树上两点简单路径的边最大权值 $ = $ Kruskal 重构树上两点 LCA 的点权。

这里我们发现，从上往下走，越往下，这个点的点权就越小，并且这个点的点权是以它为根的子树中所有点点权最大的。这道题会用到这个性质。

回到本题，我们这里需要以海拔为关键字建一棵最大生成树，所以这里的结论部分与上面的相反。总的来说就是每一个节点的祖先的权值都大于等于它的权值。

所以我们搜一个节点为起点时，我们就不断地往它的祖先走，知道点权小于等于水位线为止，再在这个节点的子树中的叶子节点中找距离一号节点最近的值。

这里可以先跑Dijkstra，再预处理出每一个节点的子树中的叶子节点中找距离一号节点最近的值。不然单次查询就是 $ O(n) $ 的。

但是这样还是过不了，时间复杂度还是 $ O(t(m\log n+Qn)) $ ，只不过常数小了很多，但仍不足以过这道题。

这里还能优化的就是在每个节点往上找祖先时，一层一层地找太慢，这里单次查找用倍增可以优化到 $ O(\log n) $ ，就先 $ O(n) $ 预处理。那么这样的时间复杂度是 $ O(t(m\log n+Q\log n)) $ ，足以通过此题。

代码

#include<bits/stdc++.h>
#include<cstring>
using namespace std;
#define int long long
#define pll pair<int,int>
const int N=4e5+5,M=8e5+5;
int head[M],head2[M],cnt,cnt2;//存图用 
int idx,S,k,Q,n,m,lans;
int p[N][25],dis[N];//分别为倍增数组和最短路距离 
int w[N],fa[N],dep[N];//分别是重构树点权、并查集数组和重构树的深度 
priority_queue<pll,vector<pll>,greater<pll> >q;//小根堆用来跑Dijkstra 
struct node//用链式前向星存图 
{
	int v,u,w,h,nxt;
}d[M],e[M];//d用来跑最短路，e用来跑Kruskal 
struct edge
{
	int v,nxt;
}a[M];//存Kruskal重构树 
int find(int x)//并查集 
{
	if(fa[x]!=x) fa[x]=find(fa[x]);//路径压缩 
	return fa[x];
}
void add1(int u,int v,int w,int h)//加边 
{
	d[++cnt].v=v;
	d[cnt].w=w;
	d[cnt].h=h;
	d[cnt].u=u;
	d[cnt].nxt=head2[u];
	head2[u]=cnt;
}
void add2(int u,int v)
{
	a[++cnt2].v=v;
	a[cnt2].nxt=head[u];
	head[u]=cnt2;
}
int read()//快读 
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool cmp(node aa,node bb){return aa.h>bb.h;}//排序 
void dijkstra(int s)//最短路 
{
	for(int i=1;i<=2*n;i++) dis[i]=2e18;//初始化 
	dis[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty())
	{
		int u=q.top().second,p=q.top().first;
		q.pop();
		if(p!=dis[u]) continue;
		for(int i=head2[u];i!=0;i=d[i].nxt)
		{
			int v=d[i].v,w=d[i].w;
			if(dis[v]>dis[u]+w) dis[v]=dis[u]+w,q.push(make_pair(dis[v],v));
		}
	}
}
void kruskal()//Kruskal重构树 
{
	idx=n;
	for(int i=1;i<=2*n;i++) fa[i]=i;//初始化并查集数组 
	for(int i=1;i<=m;i++)
	{
		int u=find(e[i].u),v=find(e[i].v),h=e[i].h;
		if(u==v) continue;
		idx++;//新节点编号 
		fa[u]=fa[v]=idx;//并查集连边 
		w[idx]=h;//更新点权 
		add2(idx,u),add2(idx,v);//建新边 
		if(idx==2*n-1) return;//退出 
	}
}
void dfs(int u,int fa)//预处理倍增 
{
	p[u][0]=fa,dep[u]=dep[fa]+1;//深度和倍增数组 
	for(int i=1;(1<<i)<=dep[u];i++) p[u][i]=p[p[u][i-1]][i-1];//倍增初始化 
	for(int i=head[u];i!=0;i=a[i].nxt)dfs(a[i].v,u),dis[u]=min(dis[u],dis[a[i].v]);//更新重构树上子树中离一号节点距离的最小值 
}
int get(int u,int s)//倍增往上跳祖先 
{
	for(int i=18;i>=0;i--) if(w[p[u][i]]>s&&(1<<i)<=dep[u]) u=p[u][i];//没有低于水位线就往上跳 
	return dis[u];//返回最小值 
}
signed main()
{
	int t=read();
	while(t--)
	{
		n=read(),m=read();
		cnt=0,cnt2=0,lans=0;//多测要清空 
		memset(head,0,sizeof(head));
		memset(head2,0,sizeof(head2));
		for(int i=1;i<=m;i++) 
		{
			e[i].u=read(),e[i].v=read(),e[i].w=read(),e[i].h=read();
			add1(e[i].u,e[i].v,e[i].w,e[i].h),add1(e[i].v,e[i].u,e[i].w,e[i].h);//连边跑最短路 
		}
		dijkstra(1);//最短路 
		sort(e+1,e+m+1,cmp);//按海拔从大到小排序 
		kruskal(); //Kruskal重构树 
		dfs(idx,0);//预处理倍增 
		Q=read(),k=read(),S=read();
		while(Q--)
		{
			int st=read(),s=read();
			st=(st+k*lans-1)%n+1;
			s=(s+k*lans)%(S+1);//强制在线求出真正的值 
			lans=get(st,s);//查询值 
			printf("%lld\n",lans);
		}
	}
	return 0;
}