51nod1298圆与三角形——(二分法)
给出圆的圆心和半径,以及三角形的三个顶点,问圆同三角形是否相交。相交输出"Yes",否则输出"No"。(三角形的面积大于0)。




Input
第1行:一个数T,表示输入的测试数量(1 <= T <= 10000),之后每4行用来描述一组测试数据。 4-1:三个数,前两个数为圆心的坐标xc, yc,第3个数为圆的半径R。(-3000 <= xc, yc <= 3000, 1 <= R <= 3000) 4-2:2个数,三角形第1个点的坐标。 4-3:2个数,三角形第2个点的坐标。 4-4:2个数,三角形第3个点的坐标。(-3000 <= xi, yi <= 3000)
Output
共T行,对于每组输入数据,相交输出"Yes",否则输出"No"。
Input示例
2 0 0 10 10 0 15 0 15 5 0 0 10 0 0 5 0 5 5
Output示例
Yes No
题意:给出一个圆的圆心坐标以及圆的半径,三角形三个顶点的坐标,问你这个三角形和圆是否有交点。
思路:这一题刚看好像挺简单,在51nod上也是0分基础题,一开始觉得三个点都在圆外或都在圆内就不相交,否则就相交,但仔细一想却并没有那么简单。顶点是否在圆内只需要判断顶点到圆心的距离是否小于半径即可。这道题要分三种情况考虑:
第一种:三角形三个点到圆心的距离均小于半径(三个点都在圆内),如下图:
由上图可知,三个点在圆内可以确定没有相交。
第二种:有至少一个点在圆上或一部分在圆内一部分在圆外,如下图:
可以确定这一种情况一定相交;
第三种:三个顶点全在圆外,这种情况比较复杂,见下图:
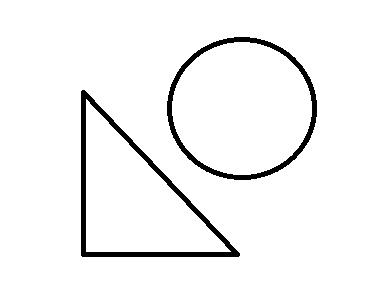
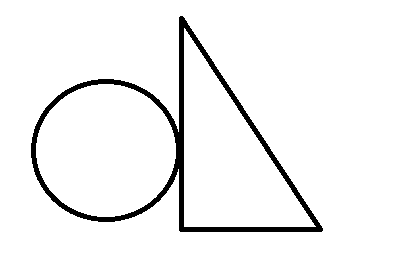
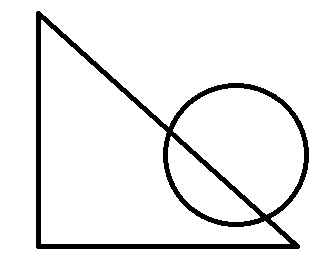
三个点都在外的主要分为这三种情况,那如何来进行判断呢?
这里可以用二分法来判断:分别用二分判断三条边,lowx,lowy,highx,highy表示边的两个端点,midx,midy表示边的中点,如果中点在圈内,那说明这条边肯定和圆有交点,因为边的端点都在圈外;如果中点在圈外,那就取线段其中的一半继续判断,取哪一半呢?我们可以想一下,如果相交,那在线段在圈内的那一段更靠近线段的哪一半,当然是端点更靠近圆心的那一半啊,就像上面的最后一张图,与左上角的端点相比,三角形右下角的端点更靠近圆心,所以相交的那一段更靠近右下角。正因为这样,我们二分时范围的改变就有了依据。二分的终止条件是什么?就是当中点与端点非常靠近时,这时可以等同于已经在端点处,无法再分了(貌似不是很严谨,但可以AC)。还有一点,当线段的两个端点的横坐标或纵坐标相等时,需要进行特判,因为横坐标相等时,中点的横坐标一直都等于端点横坐标的,这样二分可能会出现问题。下面看代码:
1 #include<iostream> 2 #include<cstdlib> 3 #include<cstring> 4 #include<cstdio> 5 #include<string> 6 #include<cmath> 7 #include<algorithm> 8 #include<stack> 9 #include<queue> 10 #define ll long long 11 #define inf 0x3f3f3f3f 12 using namespace std; 13 14 int dir[3][2] = {{1,2},{1,3},{2,3}}; //用来表示三条边,分别以(1,2)(1,3) (2,3)为边的端点 15 16 int main() 17 { 18 int t; 19 double xc,yc,r,x[5],y[5],farnode[5]; 20 cin>>t; 21 while(t--) 22 { 23 scanf("%lf%lf%lf",&xc,&yc,&r);//输入圆的坐标及半径 24 int sum1 = 0,sum2 = 0;//sum1记录三角形在圆外的端点个数,sum2记录在圆内的端点个数 25 for(int i=1; i<=3; ++i) 26 { 27 scanf("%lf%lf",&x[i],&y[i]);//输入三个端点 28 farnode[i] = (x[i]-xc)*(x[i]-xc) + (y[i] - yc)*(y[i] - yc);//记录每个端点与圆心的距离 29 if(farnode[i] > r*r) //到圆心的距离大于半径 30 sum1++; 31 else if(farnode[i] < r*r) // 到圆心的距离小于半径 32 sum2++; 33 } 34 35 if(sum2 == 3) //如果都在圆内 36 printf("No\n"); 37 else if(sum1 == 3) //如果都在圆外 38 { 39 int flag = 0; 40 double lowx,lowy,highx,highy; 41 for(int i=0; i<3; ++i) //遍历三条边 42 { 43 lowx = x[dir[i][0]]; 44 lowy = y[dir[i][0]]; 45 highx = x[dir[i][1]]; 46 highy = y[dir[i][1]]; 47 48 49 50 if(lowx == highx) //特判端点横坐标相等的情况 51 { 52 if(fabs(lowx-xc) <= r) 53 { 54 if((lowy >= yc && highy <= yc) || (lowy<= yc && highy>= yc)) 55 flag = 1; 56 } 57 } 58 59 else if(lowy == highy) //特判端点纵坐标相等的情况 60 { 61 if(fabs(lowy-yc) <= r) 62 { 63 if((lowx >=xc && highx <= xc)|| (lowx<= xc && highx>= xc)) 64 flag = 1; 65 } 66 } 67 68 else//否则二分判断 69 { 70 double midx,midy,lon,lonl,lonr; 71 midx = (lowx + highx)/2; 72 midy = (lowy + highy)/2; 73 while(midx - lowx > 0.1 || midx - lowx < -0.1) //当中点非常接近端点时结束循环 74 { 75 lon = (midx - xc)*(midx - xc) + (midy - yc)*(midy - yc);//求出中点在与圆心的距离 76 if(lon <= r*r) //如果在圆内则表示相交 77 { 78 flag = 1; 79 break; 80 } 81 lonl = (lowx - xc)*(lowx - xc) + (lowy - yc)*(lowy - yc); // 计算两个端点到圆心的距离 82 lonr = (highx - xc)*(highx - xc) + (highy - yc)*(highy - yc); 83 if(lonl > lonr) //如果右端点靠近圆心,那就继续查找线段的右边一半 84 { 85 lowx = midx; 86 lowy = midy; 87 } 88 else if(lonl < lonr) //否则查找左边一半 89 { 90 highx = midx; 91 highy = midy; 92 } 93 else break; 94 midx = (lowx + highx)/2; //继续取中点 95 midy = (lowy + highy)/2; 96 } 97 } 98 if(flag) break; 99 } 100 if(flag) printf("Yes\n"); 101 else printf("No\n"); 102 } 103 else 104 printf("Yes\n"); 105 } 106 return 0; 107 } 108 109 /* 110 3 111 -7 3 1 112 -8 -7 113 -3 9 114 -8 7 115 */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号