算法效率的度量
在对于一个算法的度量中,我们通常会使用两种方法对算法进行度量,分别是时间复杂度与空间复杂度这两个维度。
今天对于这两种度量方式做一下总结:
时间复杂度(时间维度):
对于一个程序时间复杂度我们有两种方式进行分析
事后统计法,是直接将程序在计算机上进行测试,直接得出该程序的实际跑测的时间。
事前统计分析法,是利用某些分析的框架对算法的运行时间进行估计。
对于事前估计法,现在主要的分析框架有
按照输入规模度量:
(1)时间频度:一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
(2)时间复杂度:在刚才提到的时间频度中,n称为问题的规模,当n不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。我们利用某一个辅助函数最大程度的模拟T(n)在n变化后的变化情况。
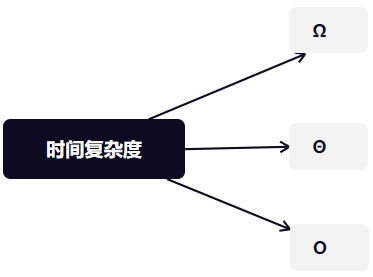
我们利用三种方式(负号)来表示或模拟时间复杂度:
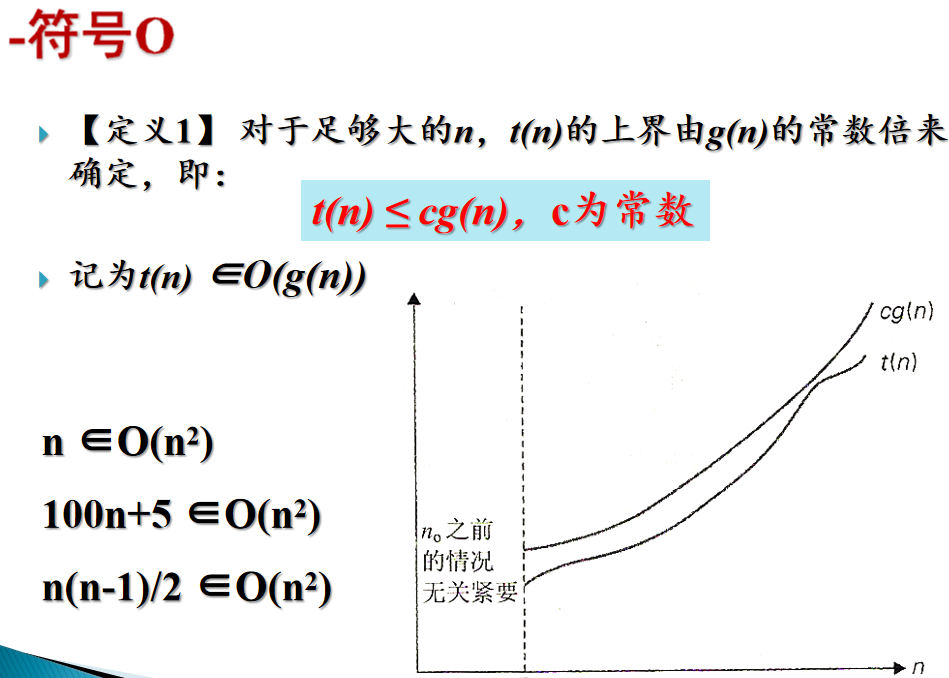
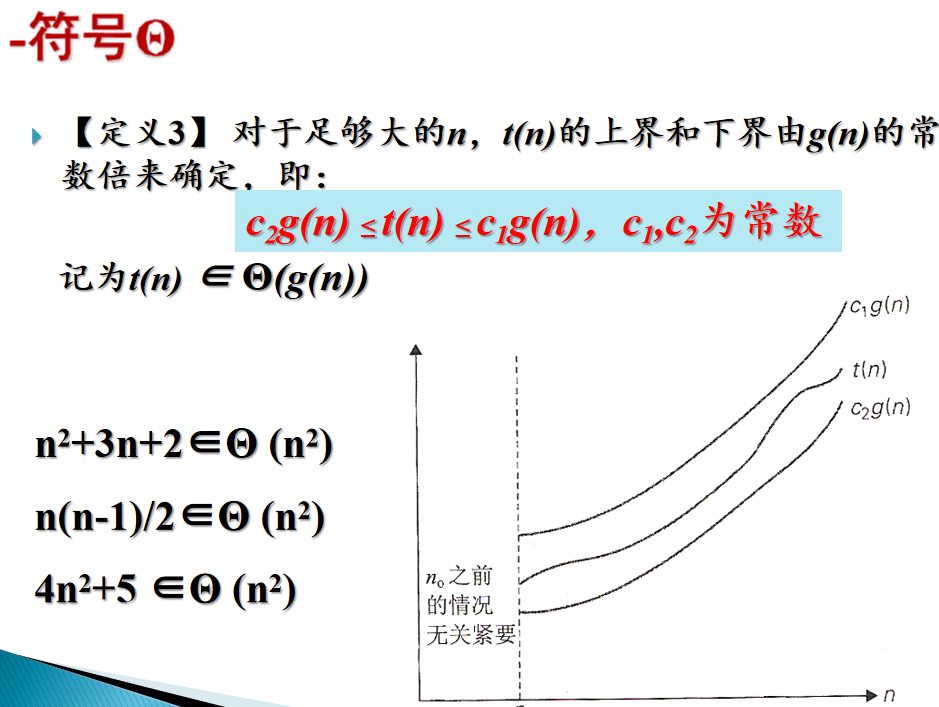

渐近时间复杂度:
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度,又称大O表示法,实际上这种表示法并不是O,而是Θ,但是在实际的引用中我们却是用O表示的渐进时间复杂度(大O表示法)而不是Θ



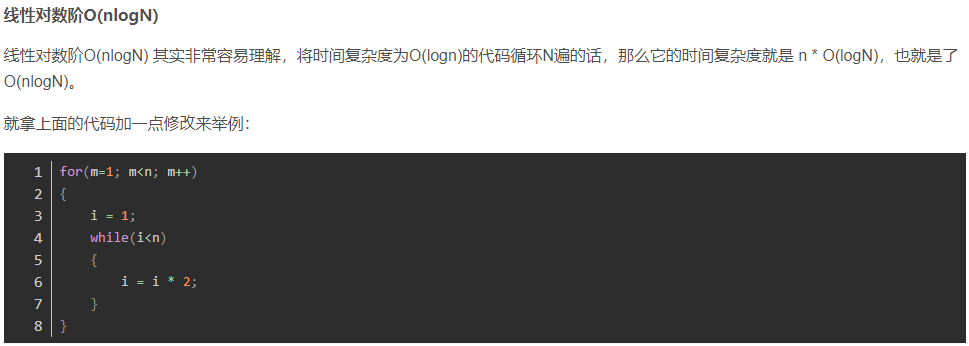

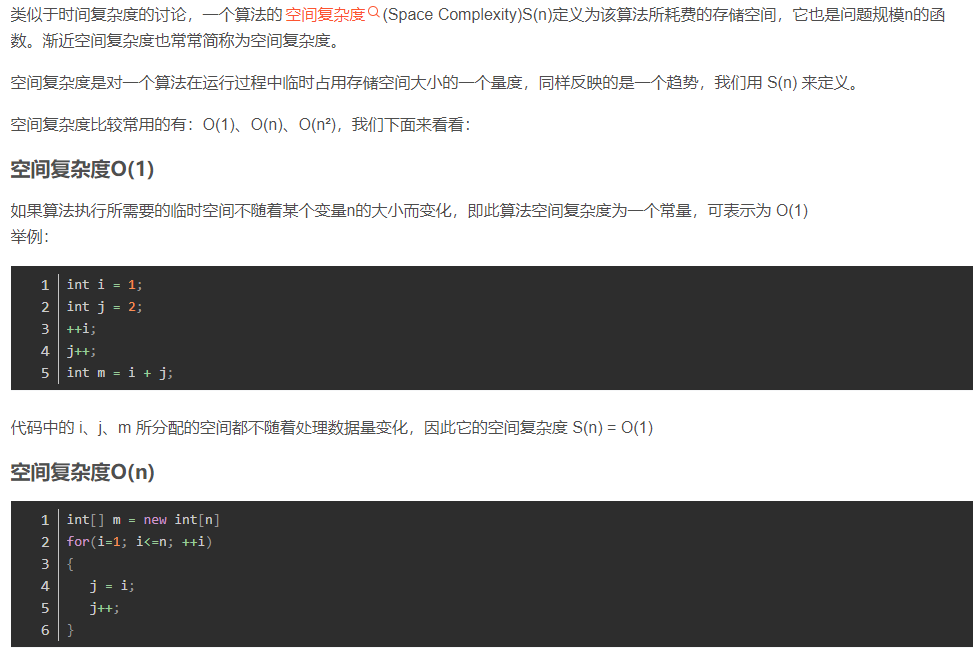
空间复杂度:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号