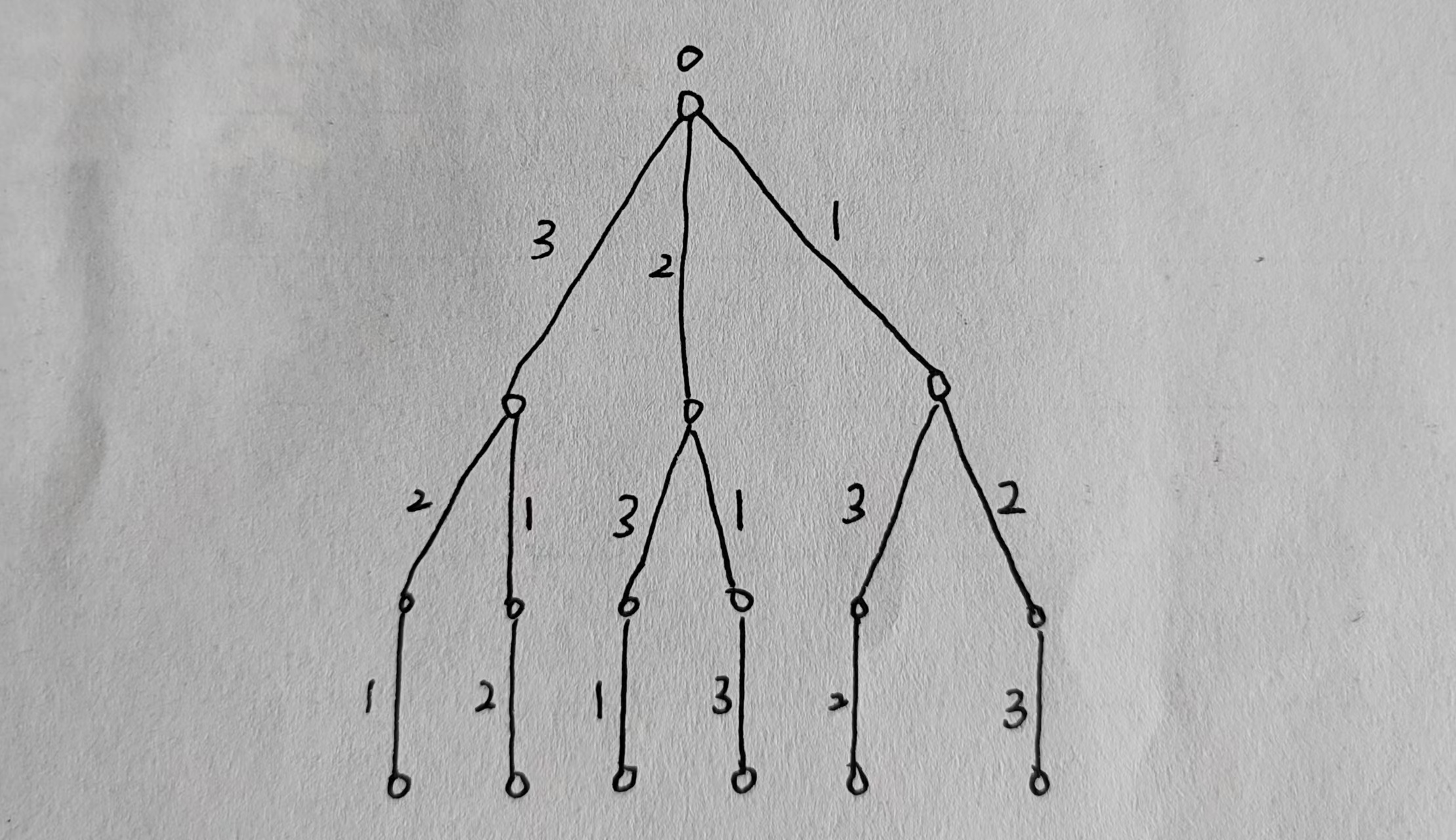
回溯法求解TSP问题

1.readme

<1>python
<2>代码基于具体的实例，如有需要可自行修改问题规模为n，不再赘述

2.code

# 代价矩阵 999表示无穷
arc = [[999, 3, 6, 7],
       [5, 999, 2, 3],
       [6, 4, 999, 2],
       [3, 7, 5, 999]]
# city 存放除出发点0外的城市
city = [1, 2, 3]
# 访问标志数组 0-未访问 1-已访问
visit = [0, 0, 0]
# 存放最短路径，首元素与尾元素为出发点0
way = [0, 0, 0, 0, 0]
# 记录当前距离
CurDistance = 0
# 记录最短路径距离，初始值999表示无穷大，找到更优解则替换
BestDistance = 999
# 标志位 判断是否走完全程
flag = 0


# 判断是否访问完所有城市
def is_empty():
    for i in visit:
        if i == 0:
            return 0
    return 1


# 更新最短路径
def way_add(x):
    for i in range(1, 4):
        if way[i] == 0:
            way[i] = x
            break


# 回溯，恢复路径
def way_out():
    for i in range(3, 0, -1):
        if way[i] != 0:
            way[i] = 0
            break


# 回溯算法函数
def back_track(n):
    if is_empty():  # 如果访问完全部城市
        global CurDistance
        global BestDistance
        if CurDistance < BestDistance:  # 判断是否是更优解，是则记录下来
            BestDistance = CurDistance
            print("最短距离:", end='')
            print(BestDistance, end=' ')
            print("BestWay:", end='')
            for i in range(0, len(way)):
                print(way[i], end='')
                if i != len(way) - 1:
                    print("-->", end='')
                if i == len(way) - 1:
                    print()
    else:
        for i in city:
            if visit[i - 1] == 0:
                visit[i - 1] = 1
                way_add(i)
                CurDistance += arc[n][i]
                if is_empty():  # 如果此时走完所有城市，还需加上回到出发点的距离，同时设置标志位
                    global flag
                    flag = 1
                    CurDistance += arc[i][0]
                if CurDistance > BestDistance:  # 剪枝函数，CurDistance>BestDistance,回溯
                    visit[i-1] = 0
                    CurDistance -= arc[n][i]
                    if flag == 1: # 如果走完所有城市，还需减去回到出发点的距离
                        flag = 0
                        CurDistance -= arc[i][0]
                    way_out()
                    return
                back_track(i)   # 向下递归
                visit[i-1] = 0  # 回溯，恢复访问标志位
                CurDistance -= arc[n][i]
                if flag == 1:
                    flag = 0
                    CurDistance -= arc[i][0]    # 回溯，恢复CurDistance
                way_out()   # 回溯，恢复路径


# 调用回溯算法函数
back_track(0)

3.result
<1>将city设置为[1,2,3]


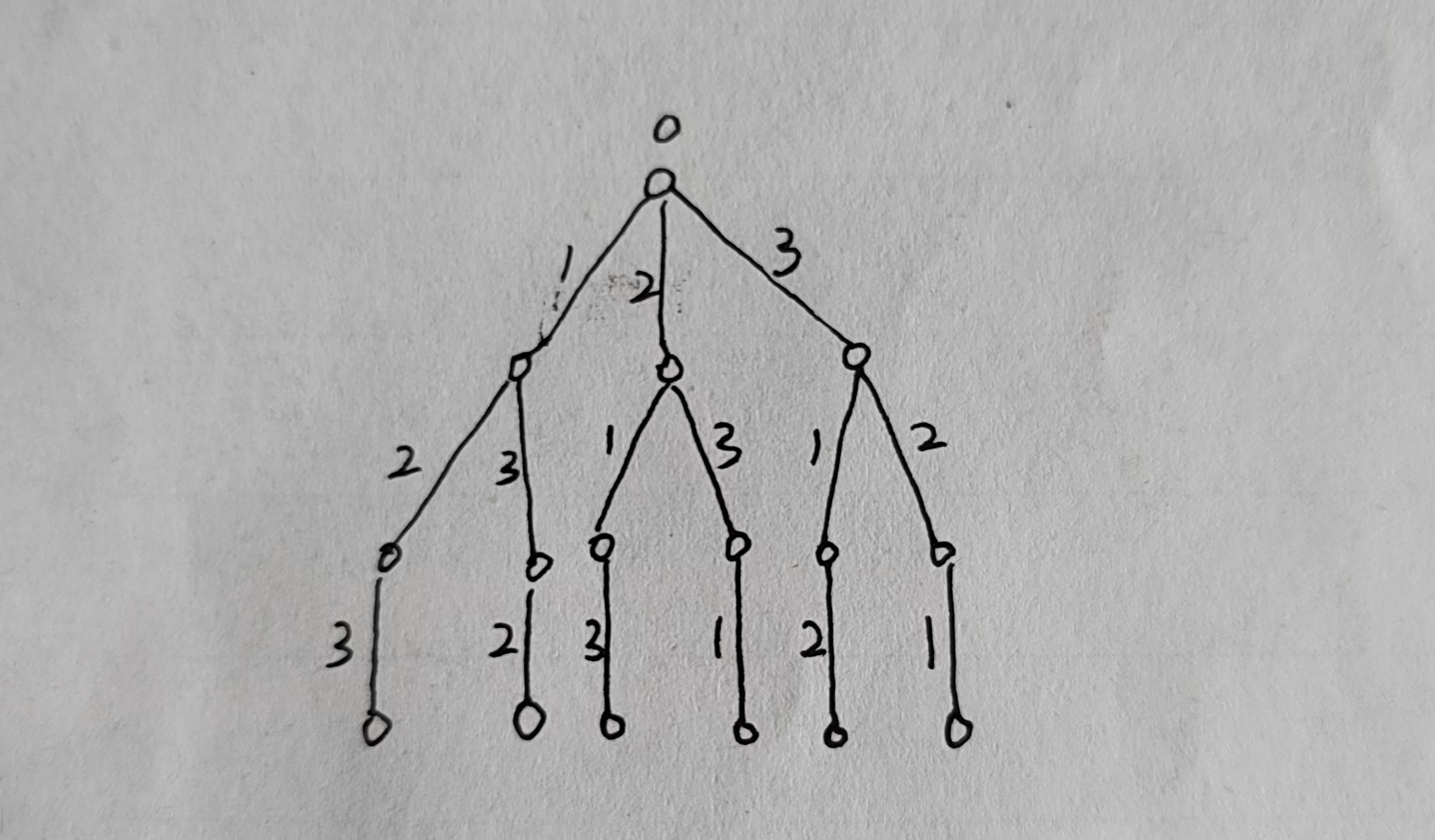
<2>将city设置为[3,2,1]