Accurate Respiration Monitoring for Mobile Users with Commercial RFID Devices

商用RFID设备用于移动用户的精确呼吸监测

• https://ieeexplore.ieee.org/document/9184900
• IEEE Journal on Selected Areas in Communications ( Volume: 39, Issue: 2, February 2021)

摘要

在本文中，我们提出了RF-RMM，一种基于rfid的方法来精确和连续的呼吸监测移动用户。移动人群呼吸监测的主要挑战是，由用户的呼吸引起的微小身体位移被用户的整个身体运动所压倒。为了解决这个问题，我们提出了一种新的方法，使用一对标签来消除用户的身体运动的影响。我们融合来自配对标签的数据，以消除用户整个身体运动的影响，只保留用户呼吸引起的位移。在实现RF-RMM时，另一个具有挑战性的问题是如何解决目标用户移动时的相位模糊问题，这个问题比静态情况下更加严重。我们提出了一种距离跟踪算法来跟踪用户运动过程中的相位变化，从而很好地解决了相位模糊问题。我们将RF-RMM应用于商用RFID设备，并进行了广泛的真实世界实验来评估其性能。结果表明，RF-RMM对不同用户呼吸速率的平均估计误差为0.54 BPM，对用户个体呼吸长度的平均相对误差小于13%，实现了对呼吸速率的准确监测。

主要贡献

• 我们提出了一种新的成对标签的方法来消除用户全身移动时对标签后向散射信号的影响。该方法可以从混合体运动中提取出仅由用户呼吸引起的位移，从而准确估计目标用户的呼吸速率。该方法还考虑了用户的方位，即使用户在随机移动时也能获得准确的呼吸监测。
• 设计了一种有效处理由用户移动引起的相位模糊问题的算法。RF-RMM需要跟踪标签和读取器天线之间的距离变化，以获得准确的呼吸监测。相位模糊可能会降低距离估计的精度，进而降低呼吸监测的精度。该算法对天线与标签之间的距离变化的跟踪精度达到厘米级，保证了对用户呼吸状态的高精度监测。
• 我们将上述想法放在一起，并在商用Impinj R420阅读器和被动标签上实现了一个RF-RMM原型。结果表明，RF-RMM的呼吸速率估计误差小于0.54 BPM，优于现有的方法。此外，RF-RMM还可以测量用户的个体呼吸持续时间，相对误差小于13%。

主要内容

射频识别呼吸监测:初步

射频识别背景

无源标签从连续的波信号中获取能量，并通过将波信号与想要传输的数据进行调制后向阅读器散射。当阅读器询问标签时，在不考虑多径效应的情况下，接收到的后向散射信号可以表示为

\(A(t)\) 信号的幅值
\(\phi(t)\) 信号的相位值

\[S(t)=A(t) e^{-j \phi(t)}\tag{1} \]

在阅读器天线接收到的信号的RSS和相位都受到标签和天线之间距离的影响。用\(d\)表示阅读器天线与标签之间的距离。\(\phi\)与\(d\)的关系可以描述为

\(\lambda\) 信号的波长
\(\theta\) 由于阅读器和标签的硬件缺陷而引起的分集项

\[\phi=\left(2 \pi \frac{2 d}{\lambda}+\theta\right) \bmod 2 \pi,\tag{2} \]

---

基于rfid的呼吸监测:基本理念

使用RFID监测用户呼吸有两种方法。在第一种方法中，被动标记被粘贴到用户的腹部或胸部。用户的呼吸会引起贴在腹部/胸部的标签与天线之间的周期性距离变化，这可以通过跟踪标签后向散射信号的相位或RSS来检测。在这种类型的方法中，可以通过使用附加到用户的标记的ID来区分多个用户。在第二种方法中，标签没有附加到用户身上，而是预先部署在用户周围的某些位置。用户的呼吸会影响标签和天线之间的信号传输。通过提取用户呼吸引起的信号变化，得到用户的呼吸量。然而，在第二种方法中，很难区分多个用户。
我们的方法采用了第一种方法，利用RFID同时监视多个用户的能力。其原理如下。如图所示，当使用者呼吸时，腹部会发生移位。当使用者吸气时，他/她的腹部和胸部会向阅读器天线移动，因此标签和天线之间的距离会缩短。相反，当用户呼气时，标签和天线之间的距离增加。根据式\((2)\)，这导致用户标签的相位读数周期性变化。通过追踪相位变化，我们可以估计使用者的呼吸速率。

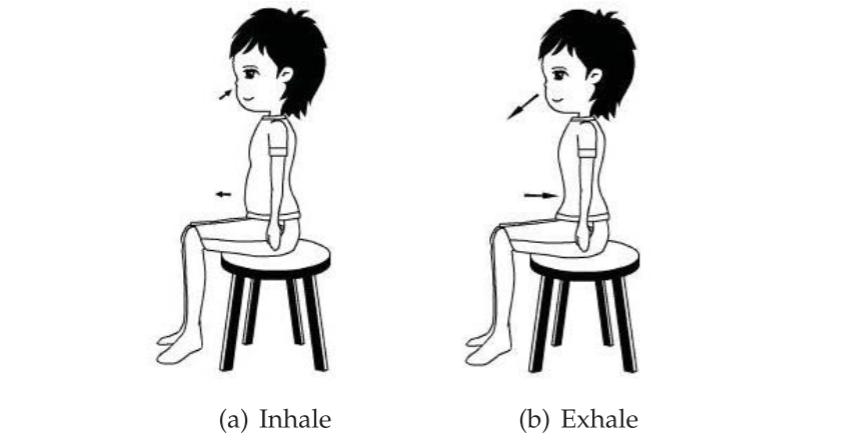
我们进行了一个实验来评估在监视过程中用户是静态的情况下这种方法的性能。在实验中，我们将一个异形AZ9654被动标签贴在用户的腹部，让他站在1.5米远的天线前面。

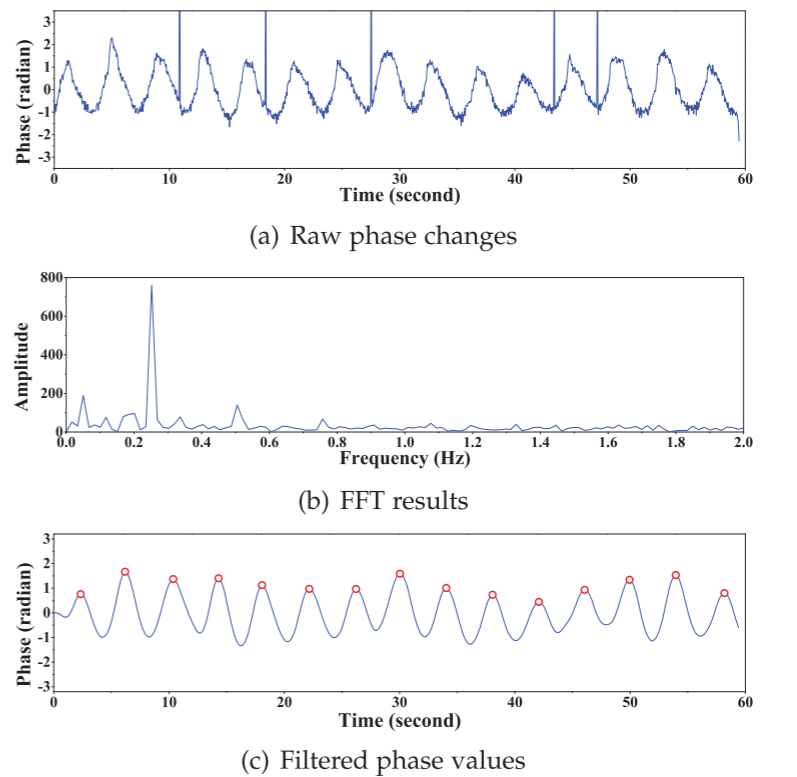
采集到的相位读数具有明显的周期性，如图(a)所示。图(b)为应用快速傅里叶变换(FFT)后相位读数的频谱。我们对[5]中提出的切割频率为0.67Hz的频谱进行Butterworth滤波，并利用快速傅里叶反变换(IFFT)将其变换回时域，得到平滑后的相位值，结果如图(c)所示。在图(c)中，我们标记了过滤后的相位值的峰值，对应于用户在呼出和吸气之间切换时的转换时间。

---

当用户移动时

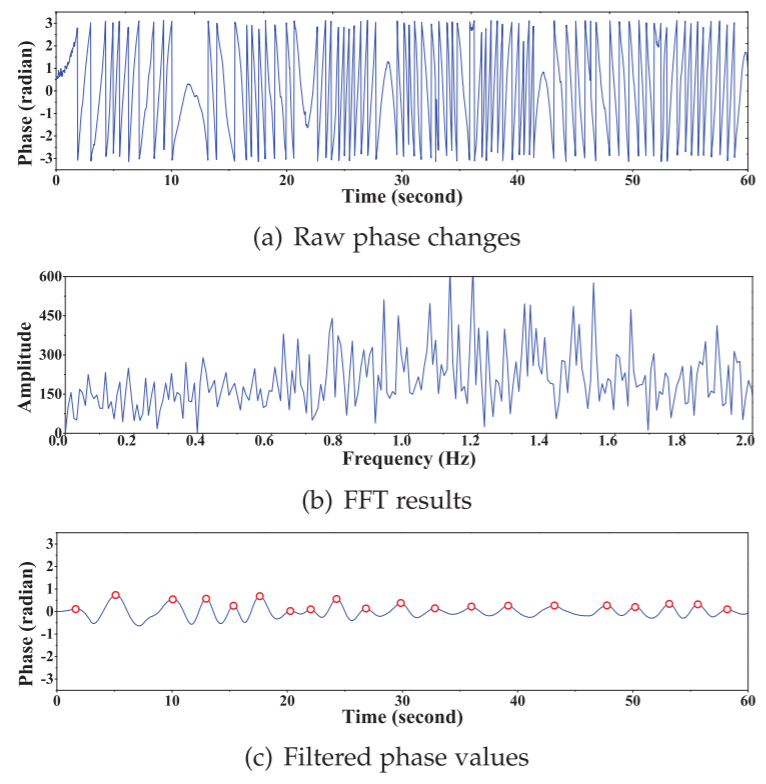
我们进行了一个实验，以显示如何移动的用户影响呼吸监测的准确性。在本实验中，我们让用户在天线前来回移动。结果如图4所示。图(a)显示了用户移动时的原始阶段读数。可以看出，相位主要受用户全身运动的影响，由用户呼吸引起的相位变化在信号中被压制。图(b)绘制了对图(a)所示相位进行FFT后的频谱。可以看出，频谱是随机分布的，没有静态情况下的主导频率(图(b)))。考虑到用户整个身体的运动在频域引起不同的频率分量，我们在频谱上采用Butterworth带通滤波器，切割频率为[0.2Hz, 0.4Hz]，结果如图(c)所示。

---

RF-RMM的设计细节

配对标签:消除移动性的影响

我们提出了一种双标签的方法来减轻用户身体运动的影响。原理如图所示。

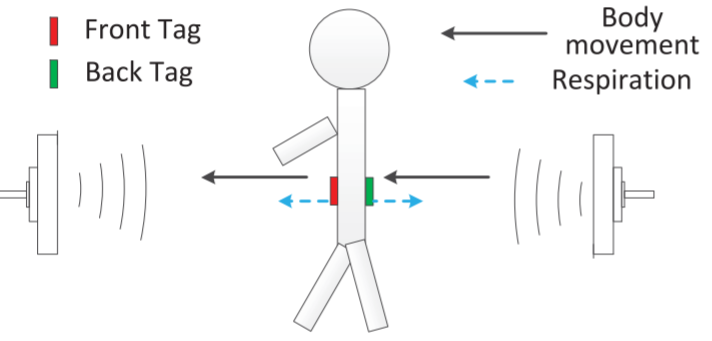
我们不是将单个标记附加到用户，而是将一对标记分别附加到用户的腹部和背部，即一个前面标记和一个后面标记。如果没有用户呼吸的影响，两个标签之间的距离不应该改变。当用户移动时，他/她的整个身体的移动会以完全相反的方式影响两个标签和相应天线之间的距离(因此影响相位)。如图6所示，d1为天线A1到前标签的距离，d2为天线A2到后标签的距离。根据式\((2)\)，我们有

\[\phi_{1}=\left(\frac{4 \pi d_{1}}{\lambda}+\theta_{1}\right)\bmod 2 \pi\tag{3} \]

和

\[\phi_{2}=\left(\frac{4 \pi d_{2}}{\lambda}+\theta_{2}\right) \bmod 2 \pi\tag{4} \]

其中\(\phi_{1}\)、\(\phi_{2}\)分别为前标签和后标签的相位读数。因此，我们有

\[d_{1}=\frac{\left(\phi_{1}+k_{1} * 2 \pi-\theta_{1}\right)}{4 \pi} \lambda, d_{2}=\frac{\left(\phi_{2}+k_{2} * 2 \pi-\theta_{2}\right)}{4 \pi} \lambda,\tag{5} \]

其中\(k_{1}\)和\(k_{2}\)是由相位模糊引起的两个整数。
如图所示，如果将用户体视为刚体，\(d_{1} + d_{1}\)应为常数。现在假设用户向\(A_{1}\)移动了一段短距离\(\Delta d\)，
然后我们有(这里我们假设\(k_{1}\)和\(k_{2}\)在\(\Delta d\)很小的时候不改变)

\[d_{1}^{\prime}=\frac{\left(\phi_{1}^{\prime}+k_{1} * 2 \pi-\theta_{1}\right)}{4 \pi} \lambda, d_{2}^{\prime}=\frac{\left(\phi_{2}^{\prime}+k_{2} * 2 \pi-\theta_{2}\right)}{4 \pi} \lambda.\tag{6} \]

我们可以将用户呼吸引起的身体位移计算为

\[\begin{aligned} \Delta r & =\left(d_{1}^{\prime}+d_{2}^{\prime}\right)-\left(d_{1}-\Delta d+d_{2}+\Delta d\right) \\ & =\lambda \frac{\left(\phi_{1}^{\prime}-\phi_{1}\right)+\left(\phi_{2}^{\prime}-\phi_{2}\right)}{4 \pi}=\frac{\lambda\left(\Delta \phi_{1}+\Delta \phi_{2}\right)}{4 \pi} . \end{aligned} \tag{7} \]

公式\((7)\)表明，通过添加两个标签阶段的相位变化，可以消除用户整个身体运动的影响。实际上，两个标签相值的总和反映了用户呼吸引起的身体位移，可以用来准确监测用户的呼吸。

然而，以上提出的方法要求用户在连接两根天线的直线上移动。在本文中，我们放松了这个约束，并提出了RF-RMM，它可以在用户随机移动的情况下精确跟踪用户呼吸引起的位移。

当用户在平行线上移动时

我们首先考虑一个简单的情况，当用户在与连接两根天线的线平行的线上移动，如图所示。

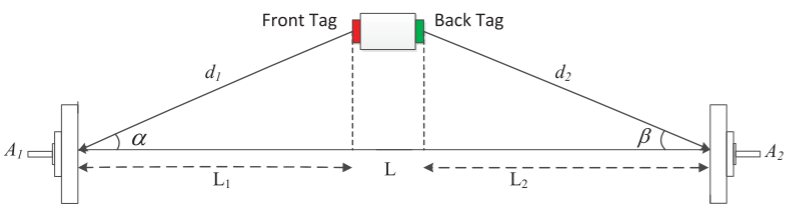
由图可知

\[L_{1}=d_{1} * \cos \alpha, L_{2}=d_{2} * \cos \beta,\tag{8} \]

其中\(d_{1}\)和\(d_{2}\)是根据式\((5)\)计算的，那么两个标签之间的距离可以计算为

\[W=L-L_{1}-L_{2} \text {. }\tag{9} \]

\(W\)的变化反映了用户呼吸引起的位移。

当用户随机移动

当用户随机移动时如图所示，

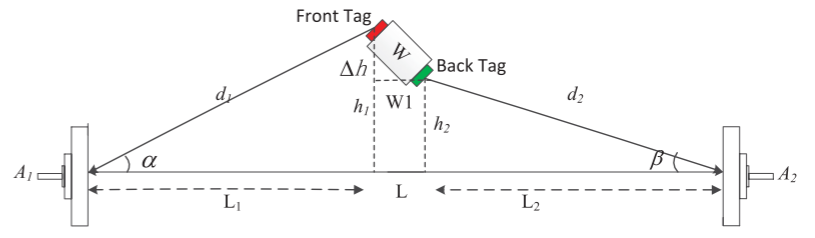
我们应该考虑用户的朝向，以准确估计呼吸引起的身体位移。我们有

\[W_{1}=L-d_{1} \cos \alpha-d_{2} \cos \beta \text {. }\tag{10} \]

用\(h_{1}\)表示前标签到连接两根天线的线之间的距离，则有

\[h_{1}=d_{1} * \sin \alpha .\tag{11} \]

类似地，后面标签到线之间的距离，在图中表示为\(h_{2}\)，可以计算为

\[h_{2}=d_{2} * \sin \beta .\tag{12} \]

这样我们可以将两个标签之间的距离修正为

\[W=\sqrt{\left(W_{1}\right)^{2}+\Delta h^{2}},\tag{13} \]

其中

\[\Delta h=\left|h_{1}-h_{2}\right|\tag{14} \]

然后通过跟踪\(W\)的变化，我们可以得到用户呼吸引起的位移。

船首方向计算

在RF-RMM中，我们需要知道标签和天线之间的角度来计算\(W\)(式\((9)\)和式\((13)\))。在本节中，我们将讨论如何计算所需的角度。
为了计算角度，我们为每个标签使用两个天线。如图所示，

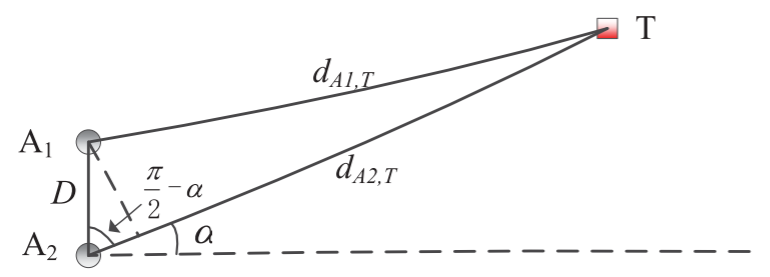
标签放置在\(T\)位置，两根天线分别放置在\(A_{1}\)和\(A_{2}\)位置。用d表示两根天线之间的距离，设\(d_{A_{1}, T}\)分别为\(A_{1}\)到\(T\)的距离，\(d_{A_{2}, T}\)分别为\(A_{2}\)到\(T\)的距离。当标签与两个天线之间的距离远远大于\(D\)(\(\left(d_{A_{1}, T} \gg D\right.\)和\(\left.d_{A_{2}, T} \gg D\right)\))时，我们有

\[\Delta d=d_{A_{1}, T}-d_{A_{2}, T} \approx D \cos (\pi / 2-\alpha)=D \sin \alpha .\tag{15} \]

因此，角\(\alpha\)可以计算为

\[\alpha=\arcsin \frac{\Delta d}{D}\tag{16} \]

但是，由于阅读器只能报告标签的相位值，所以我们还需要知道系数\(k\)才能计算标签与天线的距离，如式\((5)\)所示。其中\(\phi_{A 1, T}\)表示天线\(A_{1}\)报告的相位值，\(\phi_{A 2, T}\)表示天线\(A_{2}\)报告的相位值。根据式\((5)\)，我们有

\[d_{A_{1}, T}=\frac{\left(\phi_{A 1, T}+k_{A 1, T} * 2 \pi-\theta_{T}\right)}{4 \pi} \lambda \tag{17} \]

\[d_{A_{2}, T}=\frac{\left(\phi_{A 2, T}+k_{A 2, T} * 2 \pi-\theta_{T}\right)}{4 \pi} \lambda,\tag{18} \]

其中\(k_{A 1, T}\)和\(k_{A 2, T}\)是由相位模糊引起的两个整数。可以计算出

\[\Delta d=\frac{\lambda}{4 \pi}\left(\left(\phi_{A 1, T}-\phi_{A 2, T}\right)+2 \pi\left(k_{A 1, T}-k_{A 2, T}\right)\right) .\tag{19} \]

上式中，\(\phi_{A 1, T}\)和\(\phi_{A 2, T}\)是我们可以从阅读器的报告中直接得到的相位读数。而\(k_{A 1, T}\)和\(k_{A 1, T}\)是两个未知整数，分别对应于标签到天线的距离。我们需要知道它们来计算角度。

距离跟踪

RF-RMM不需要获取标签的准确位置;它只需要知道标签和天线之间的距离。在本节中，我们提出了一种距离跟踪算法来跟踪标签和天线之间的距离变化。根据式\((5)\)，如果知道相应的系数\(k\)(我们忽略分集项\(\theta\)，因为它的影响可以消除)，就可以计算出距离。因此，我们首先获取每个标签的k的初始值，然后使用算法跟踪\(k\)在用户移动时的变化。

获取\(k\)的初始值

方法是让用户从一个固定的位置开始。由于位置是固定的，所以可以计算出它到天线的距离，\(k\)的值可以根据式\((5)\)来计算。

跟踪\(k\)的变化

在知道\(k\)的初始值后，我们可以利用相位读数跟踪k的变化来跟踪距离的变化。目前的商用阅读器读取标签的速度可以达到每秒400个标签以上，这意味着连续两次读取一个标签的时间间隔小于0.01秒。
在这么短的时间内，用户的整个身体的移动都会小于1cm，在大多数时间内不会引起相变。(注意，当用户位移\(\lambda / 2\)，大约16.5厘米时，就会发生相变。)因此，通过跟踪相位读数的变化，我们可以确定\(k\)在哪个点应该改变，并相应地更新\(k\)的值。跟踪距离变化和更新\(k\)的算法如算法1所示。

算法1 距离跟踪算法
需要:相位读数\(\phi\)，初始\(k\)，分集项\(\theta\);
获得:距离\(d\);
1: 解决相位歧义和平滑相位读数;
2: 跟踪相位读数的变化;
3: if \(\phi\)减小，发生相变(\(0→2\pi\)) then
4: \(k = k − 1;\)
5: end if
6: if \(\phi\)增大时，发生相变(\(2\pi→0\)) then
7: \(k = k + 1;\)
8: end if
9: 根据式\((5)\)计算\(d\)

为了知道\(k\)的值应该在什么时候更新，我们使用一个窗口(第2行)跟踪相位读数的变化方向。相位读数的下降意味着标签正在靠近天线移动。在这种情况下，存在一个相变，即，相位减小到\(\theta\)，然后跳到接近2\(\pi\)，我们将\(k\)减少1(3-5行)。相反，相位读数的增加意味着标签正在远离标签。在这种情况下，当有一个相变时，即，相位增加到2\(\pi\)，然后跳到接近\(\theta\)，我们将\(k\)增加1(第6-8行)。在其他情况下，\(k\)的值保持不变，因为标签位移不足以引起相变。

把以上所有的整合在一起

RF-RMM的整体设置如图1所示。

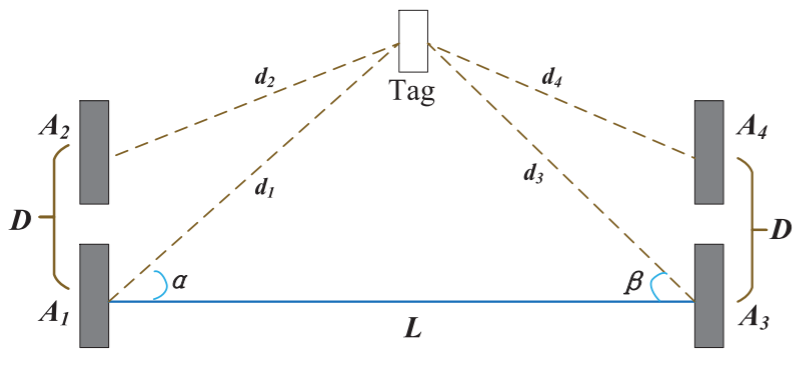
注意，由于我们使用两个标签，每个标签需要两个天线来计算其角度，因此我们总共使用了四个天线。虽然目前的RFID阅读器(如Impinj R420)可以同时控制多达4个天线，但为了减少不同天线之间的干扰，我们使用了两个阅读器，每个阅读器连接到两个天线。为了进一步减少干扰，我们让一个读取器以一个频率(922.625 MHz)询问前标签，让另一个读取器以另一个频率(921.625 MHz)询问后标签。

呼吸信号提取

相位读数采集完成后，利用算法1计算出相应的距离，根据该算法可以计算出角度α和β。然后通过式(13)计算出用户呼吸\((W)\)引起的身体位移。然后从得到的W序列中提取呼吸信号，如下所示。

数据平滑与滤波

在得到\(W\)序列后，我们先用FFT将其变换到频域，然后应用低通滤波器滤除噪声。注意到人类的呼吸频率通常小于40次/分钟1，我们使用剪切频率为0.67 Hz的Butterworth低通滤波器来过滤高频成分。高频成分通常是由多路径和环境障碍引起的。在频域滤除噪声后，利用IFFT将信号变换回时域。

呼吸速率估算

在对数据进行过滤和平滑处理后，我们估计呼吸速率如下。首先，我们找到被过滤数据的峰谷。假设有\(N\)个峰和\(M\)个谷。用\(T_{i}^{p}(0 \leq i \leq N-1)\)表示第\(i\)个峰的时间，用\(T_{j}^{v}(0 \leq j \leq M-1)\)表示第\(j\)个谷的时间。呼吸速率是用每分钟呼吸的次数来测量的，可以用高峰或低谷来计算

\[R_{p}=\frac{N-1}{T_{N-1}^{p}-T_{0}^{p}}, R_{v}=\frac{M-1}{T_{M-1}^{v}-T_{0}^{v}},\tag{20} \]

其中，\(R_{p}\)和\(R_{v}\)分别是用波峰和波谷计算的呼吸速率。将这两个值取平均值，可以减小估计误差，从而计算出最终呼吸速率为

\[R_{r}=\frac{R_{p}+R_{v}}{2}\tag{21} \]

除了呼吸频率外，我们还可以计算每次呼吸的长度。例如，对于获得的峰值，第\(i\)次呼吸的长度为

\[L P(i)=T_{i+1}^{p}-T_{i}^{p}\tag{22} \]

其中\(0 \leq i \leq N-1\)。类似地，第\(j\)次呼吸的长度也可以通过使用所得到的谷值来计算

\[L V(j)=T_{j+1}^{v}-T_{j}^{v}\tag{23} \]

其中\(0 \leq j \leq M-1\)。然而，不同于呼吸频率，个人呼吸的长度不应该被平均，因为他们实际上测量的是不同的呼吸。我们可以用\(L P\)或\(L V\)来测量个人呼吸的长度。