AVL二叉平衡树

AVL 树就是在 BST 树的基础上，引入了 “节点平衡” 的概念，即任意一个节点的左右子树的高度差不超过 1，为了维持节点的平衡，引入了四种旋转操作：

1. 左孩子的左子树太高，进行【右旋】操作；
2. 右孩子的右子树太高，进行【左旋】操作；
3. 左孩子的右子树太高，进行【左-右旋转】操作，也叫【左平衡】操作；
4. 右孩子的左子树太高，进行【右-左选择】操作，也叫【右平衡】操作；

其中，右旋操作及其代码如下图所示，由于蓝色节点在旋转前位于 node 节点的左子树，根据 BST 树的性质，蓝色节点上的值均小于 node 节点，故在旋转后其位于 node 节点的左子树，以保持 BST 树的性质：

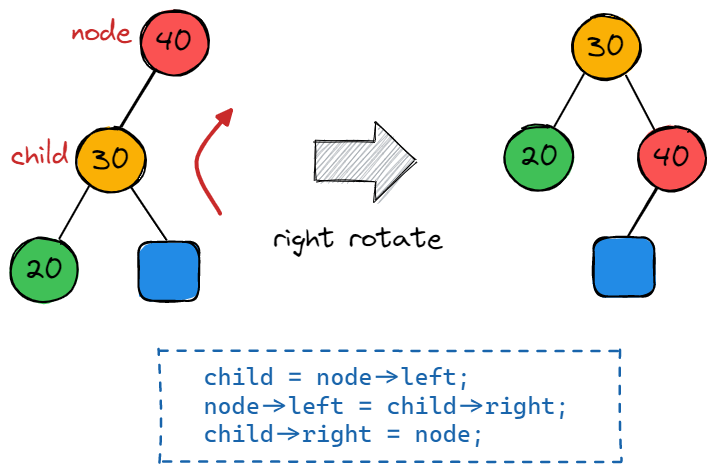
其左旋操作的示意图如下所示，与右旋操作类似，由于蓝色节点在旋转之前位于 node 节点的右子树，所以其值均大于 node 节点，所以在旋转后应将其放置于 node 节点的右子树上以维持 BST 树的性质：

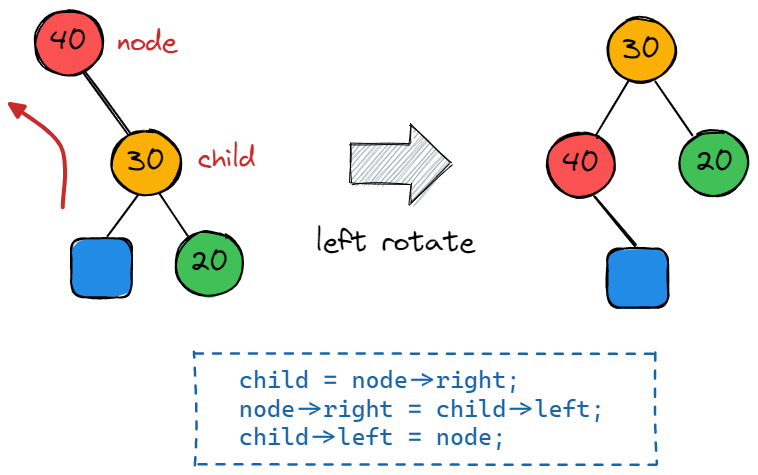
当左孩子的右子树太高时，如果我们只做一次右旋操作，那么依然无法将其变为平衡树，因此此时我们需要做两次旋转操作，先对左子树局部进行左旋操作，然后对整体进行一次右旋操作，如下图所示：

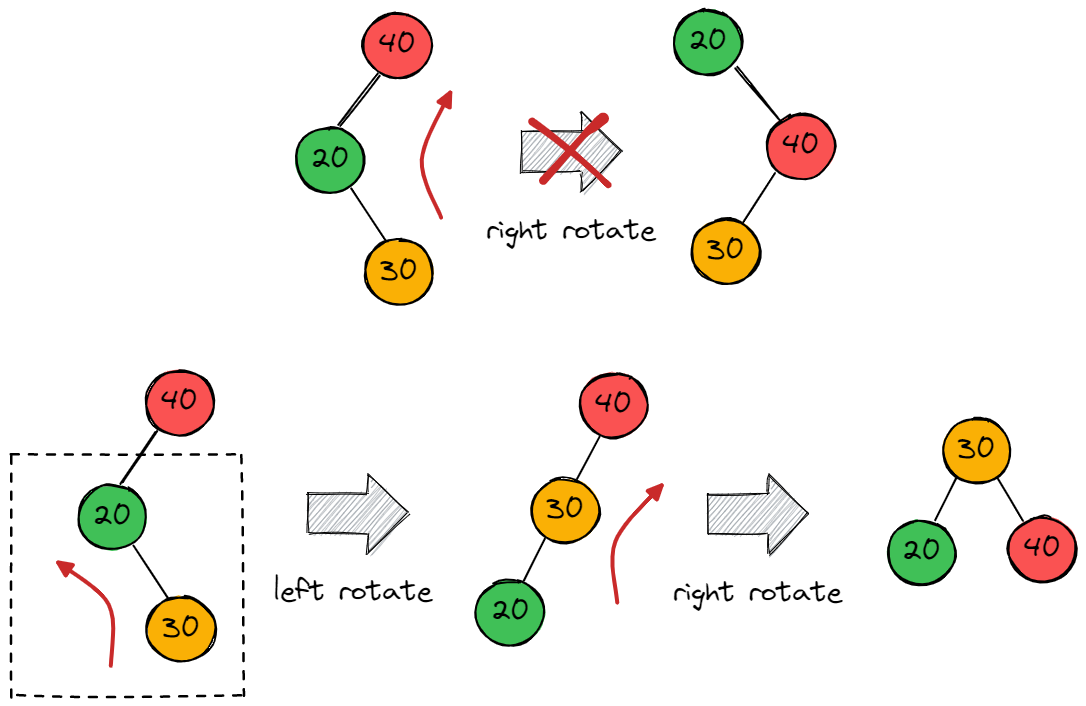
同样的，当右孩子的左子树太高时，需要执行两步操作，先对右子树的局部进行右旋操作，然后对整体进行一次左旋操作，如下图所示：

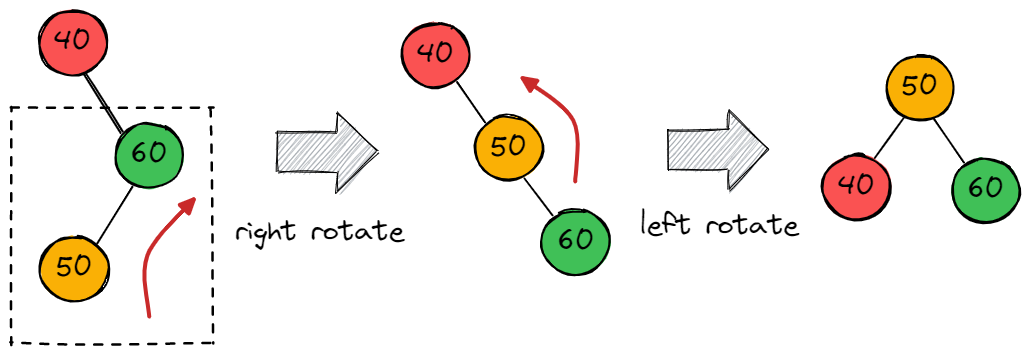
上述四种操作的代码实现如下：

// 对node做右旋转操作并将旋转后的根节点返回
Node* rightRotate(Node* node) {
	// 节点旋转
	Node* child   = node->left_;
	node->left_   = child->right_;
	child->right_ = node;
	// 更新高度
	node->height_  = max(height(node->left_), height(node->right_)) + 1;
	child->height_ = max(height(child->left_), height(child->right_)) + 1;
	return child;
}
 
// 对node做左旋转操作并将旋转后的根节点返回
Node* leftRotate(Node* node) {
	// 节点旋转
	Node* child  = node->right_;
	node->right_ = child->left_;
	child->left_ = node;
	// 更新高度
	node->height_  = max(height(node->left_), height(node->right_)) + 1;
	child->height_ = max(height(child->left_), height(child->right_)) + 1;
	return child;
}
 
// 左平衡操作
Node* leftBalance(Node* node) {
	node->left_ = leftRotate(node->left_);
	return rightRotate(node);
}
 
// 右平衡操作
Node* rightBalance(Node* node) {
	node->right_ = rightRotate(node->right_);
	return leftRotate(node);
}

对于 AVL 树的插入操作而言，它是在 BST 树插入操作的基础上，在递归的过程中，不断调整树的平衡同时更新相应节点的高度，其代码实现如下：

Node* insert(Node* node, const T& val) {
	if (node == nullptr) return new Node(val);
	
	if (node->data_ > val) {
		node->left_ = insert(node->left_, val);
		// 如果当前节点的左子树太高
		if (height(node->left_) - height(node->right_) > 1) {
			if (height(node->left_->left_) >= height(node->left_->right_)) {
				// 如果左孩子的左子树太高
				node = rightRotate(node);
			} else {
				// 如果左孩子的右子树太高
				node = leftBalance(node);
			}
		}
	} else if (node->data_ < val) {
		node->right_ = insert(node->right_, val);
		// 如果当前节点的右子树太高
		if (height(node->right_) - height(node->left_) > 1) {
			if (height(node->right_->right_) >= height(node->right_->left_)) {
				// 如果右孩子的右子树太高
				node = leftRotate(node);
			} else {
				// 如果右孩子的左子树太高
				node = rightBalance(node);
			}
		}
	}
	
	// 递归回溯时 更新节点高度
	node->height_ = max(height(node->left_), height(node->right_)) + 1;
	
	return node;
}

同样的，其删除操作也是在 BST 树删除操作的基础上，在递归的过程中，不断调整树的平衡，同时更新相应节点的高度，其代码实现如下：

Node* remove(Node* node, const T& val) {
	if (node == nullptr) return nullptr;
	
	if (node->data_ > val) {
		node->left_ = remove(node->left_, val);
		// 左子树删除节点 可能造成右子树太高
		if (height(node->right_) - height(node->left_) > 1) {
			if (height(node->right_->right_) >= height(node->right_->left_)) {
				// 右孩子的右子树太高
				node = leftRotate(node);
			} else {
				// 右孩子的左子树太高
				node = rightBalance(node);
			}
		}
	} else if (node->data_ < val) {
		node->right_ = remove(node->right_, val);
		// 右子树删除节点 可能造成左子树太高
		if (height(node->left_) - height(node->right_) > 1) {
			if (height(node->left_->left_) >= height(node->left_->right_)) {
				// 左孩子的左子树太高
				node = rightRotate(node);
			} else {
				// 左孩子的右子树太高
				node = leftBalance(node);
			}
		}
	} else {
		// 找到待删除节点
		// 情况3: 左子节点和右子节点均不为空
		if (node->left_ != nullptr && node->right_ != nullptr) {
			// 避免删除前驱或者后继节点造成节点失衡 谁高删谁
			if (height(node->left_) >= height(node->right_)) {
				// 删除前驱节点
				Node* pre = node->left_;
				while (pre->right_ != nullptr) {
					pre = pre->right_;
				}
				node->data_ = pre->data_;
				node->left_ = remove(node->left_, pre->data_);
			} else {
				// 删除后继节点
				Node* nxt = node->right_;
				while (nxt->left_ != nullptr) {
					nxt = nxt->left_;
				}
				node->data_  = nxt->data_;
				node->right_ = remove(node->right_, nxt->data_);
			}
		} else {
			// 情况1或情况2: 最多只有一个节点不为空
			if (node->left_ != nullptr) {
				Node* left = node->left_;
				delete node;
				return left;
			} else if (node->right_ != nullptr) {
				Node* right = node->right_;
				delete node;
				return right;
			} else {
				return nullptr;
			}
		}
	}
	
	// 在回溯的过程中更新节点高度
	node->height_ = max(height(node->left_), height(node->right_)) + 1;
	
	return node;
}

完整的代码实现见：Kohirus-Github