KMP

感谢 @奇乐编程学院 的图。

KMP 算法，是一种利用已经知道的信息来避免重复运算的字符串匹配算法。

KMP 的算法流程

对于字符串匹配，暴力算法是一位一位的比较，但不同时，将起始指针加 $1$。然后继续匹配，复杂度为 $\mathcal {O} (nm)$。

那我们就想，再没有匹配上的这一位之前的所有位都走过了，真的有必要按暴力走吗？

我们定义一个 $nxt$ 数组，$nxt_i$ 表示前 $i - 1$ 位中 最长的公共前后缀 的长度。

那为什么要这样设计呢？

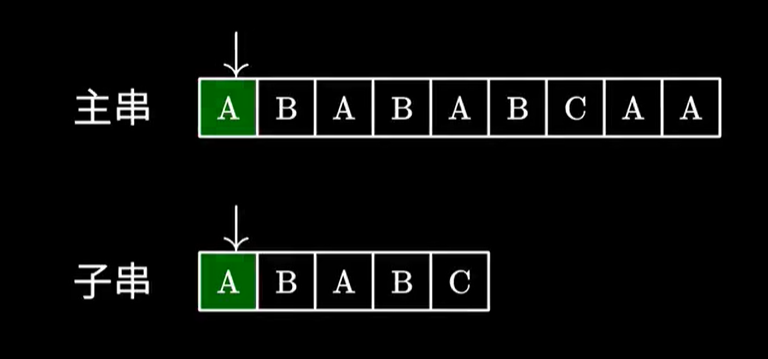
比如这张图，当你往下匹配的时候。

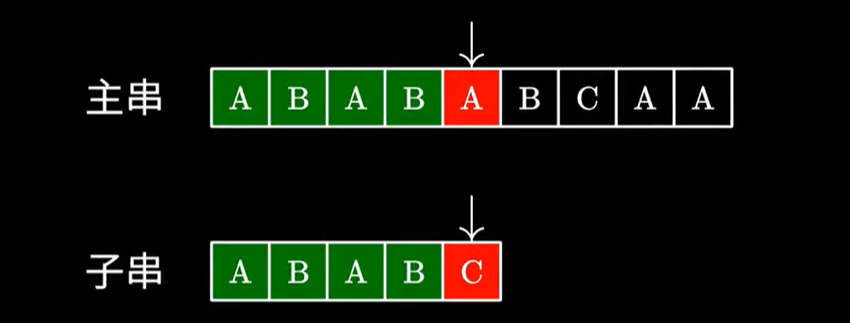
发现到了 $C$ 不匹配了，我们可以将子串移动到这个位置：

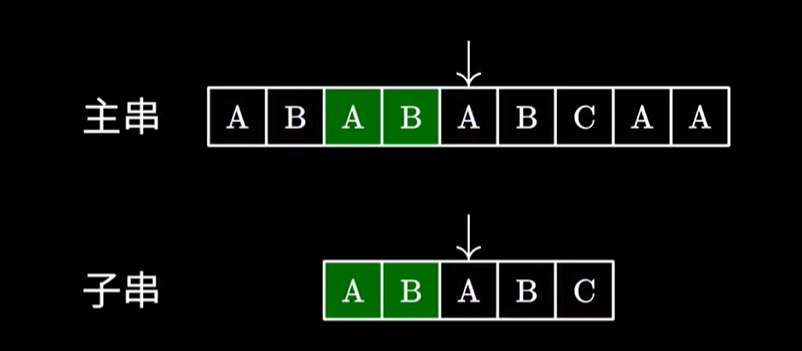
为什么这样移动是对的，你发现 $C$ 前面的最长公共前后缀是 $AB$，而之前的 $AB$ 已经匹配上了。

你这一段的后缀是和前缀相等的，而后缀已经匹配成功了，那前缀和他相等，是不是也匹配成功了，那不是就不需要匹配了吗？

直接跳过来就行了。

nxt 数组的求法

那问题来了，怎样去求解这个 $nxt$ 数组，这也是 KMP 的难点。

求 $nxt$ 数组就是在子串中找出所有 $i - 1$ 的公共前后缀长度，如果这一步用暴力求解，那这就不能保证他的复杂度为 $\mathcal{O}(n + m)$了。

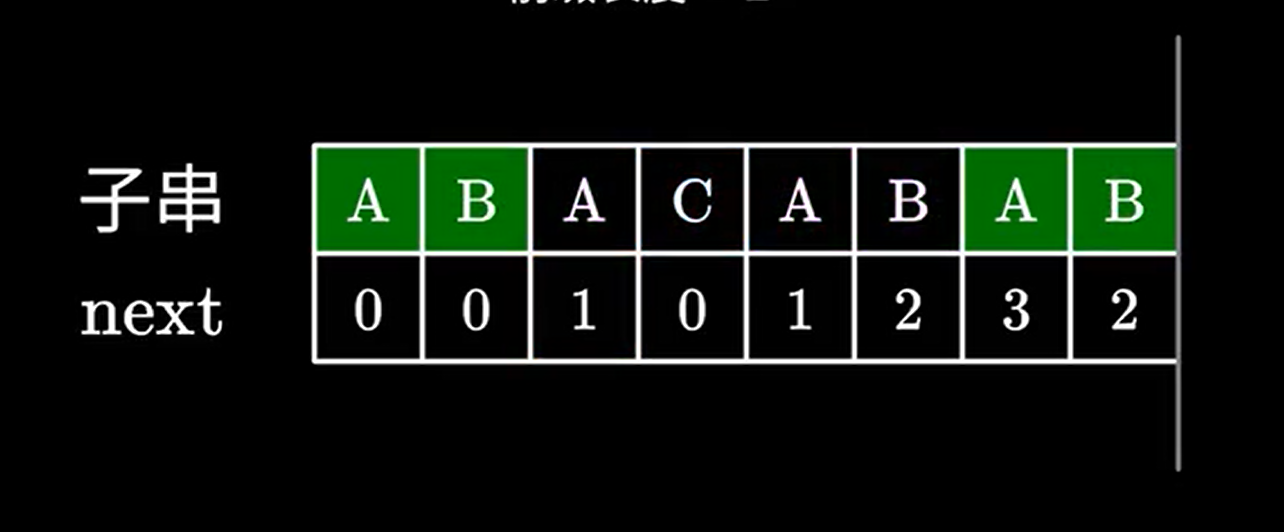
比如这个字串，假如我们当前已经匹配到了 $ABACAB$。

当指针往右移动，发现还是匹配的，那长度不久等于之前的加 $1$ 吗。

如果不匹配了，那当前这个构不成最长的，那我找个比他短的不就行了吗。

举个例子：

现在我们匹配到了 $ABACABA$ 指针向右一看，$B$ 和 $C$ 不匹配，而我们已经匹配完了 $ABACABA$。

这时的最长的公共前后缀为 $ABA$。

因为前缀和后缀是完全相等的，那 前缀的后缀 和 后缀的后缀 也是完全相等的。

我们可以直接找他前缀的最长的前后缀不就行了吗？

代码实现：

 
void kmp() {
	j = 0; // j 是子串的指针
	for(int i = 2; i <= Len2; i++) { // 这里从 $2$ 开始循环的原因是 $nxt_1$ 一定是 $0$，因为如果他遍历过的只有 $1$ 位。
		while(j && ch[i] != ch[j + 1]) j = nxt[j]; // 当不匹配的时候往前跳。
		if(ch[i] == ch[j + 1]) j++; 匹配的时候直接加
		nxt[i] = j; 
	}
}

	for(int i = 1; i <= Len1; i++) {
		while(j && s[i] != ch[j + 1]) j = nxt[j];
		if(s[i] == ch[j + 1]) j++;
		if(j == Len2) printf("%d\n", i - Len2 + 1), j = nxt[j];
	}

同理可得。