单调栈

单调栈

就是一个栈，不过栈内元素保证单调性。即，栈内元素要么从小到大，要么从大到小。而单调栈维护的就是一个数前/后第一个大于/小于他的数。

如何维护的，谁把他删了谁就是答案。

例如这组数据

5
1 4 2 3 5

来求每个数后面的比他大的值。

我们从从后往前枚举，从后往前的原因是我要考虑每个数后面的数，所以这样枚举。

我们维护一个栈，保证这个栈是单调递增的。

也就是栈顶是最小的元素。

我们加入一个元素的时候，他如果比栈顶大，那这个栈顶的元素就没用了，不断的弹出，一直弹到栈顶比他大。

然后再加入他就行了。

int n, stc[3 * N], a[3 * N], ans[3 * N];
int sc = 0;
signed main() {
	n = read();
	for(register int i = 1; i <= n; ++i) a[i] = read();
	for(register int i = n; i >= 1; --i) {
		while(sc && a[stc[sc]] <= a[i]) --sc;
		ans[i] = sc != 0 ? stc[sc] : 0;
		stc[++sc] = i;
	}
	for(register int i = 1; i <= n; ++i) print(ans[i]), putchar(' ');
}

来道例题：

P1823 [COI2007] Patrik 音乐会的等待

用一个单调栈来维护，当前的数要加到栈里，比他小的数都可以使大于等于他的数与他产生一个贡献。

注意当相同的时候要统计出现的个数。

/*
	Work by: TLE_Automation
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
#define int long long
using namespace std;

const int N = 1e6 + 10;
const int MAXN = 2e5 + 10;

inline char readchar() {
	static char buf[100000], *p1 = buf, *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int read() {
#define readchar getchar
	int res = 0, f = 0;char ch = readchar();
	for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
	for(; isdigit(ch); ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
	return f ? -res : res;
}

inline void print(int x) {
	if (x < 0 ) putchar('-'), x = -x;
	if (x > 9 ) print(x / 10);
	putchar(x % 10 + '0');
}

int n, sc = 0, ans = 0;

struct node {
	int high, num;
}x, stc[N];

signed main() {
	n = read();
	for(int i = 1; i <= n; i++) {
		x.high = read(), x.num = 1;
		while(sc && stc[sc].high <= x.high) {
			if(stc[sc].high == x.high) x.num += stc[sc].num;
			ans += stc[sc].num;
			--sc;
		}
		if(sc) ans++;
		stc[++sc] = x;
	}
	cout <<ans;
}

P4147 玉蟾宫

我们考虑枚举行来找最大面积的矩形。

我们先预处理出每行每列往上能延伸的最多的 F 的个数。

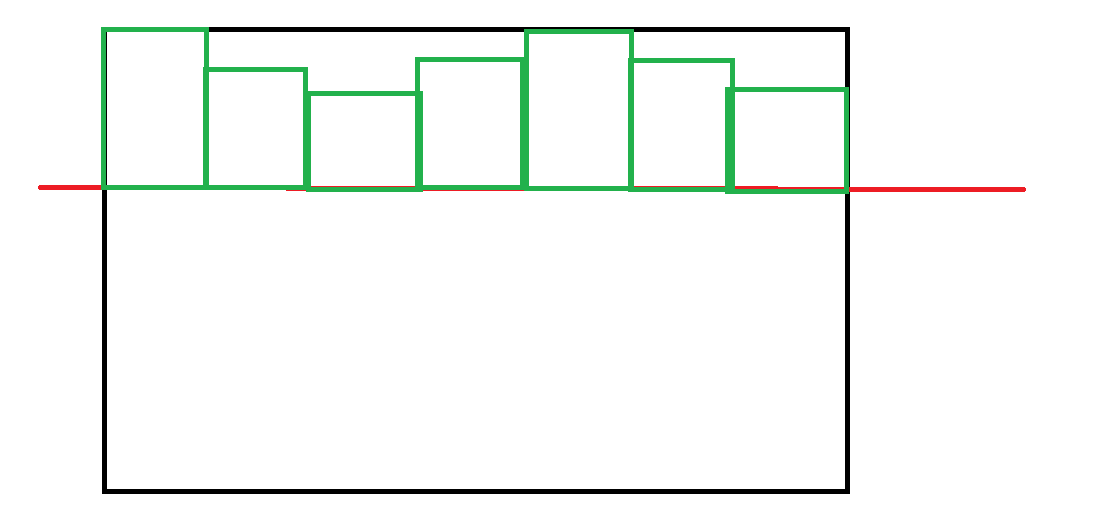
红线是枚举的悬线，求最大面积就是维护一个递减的栈，所以我们可以采用单调栈来做。

对于栈里的每一个元素，我们保存他的高度和能维护的宽度。

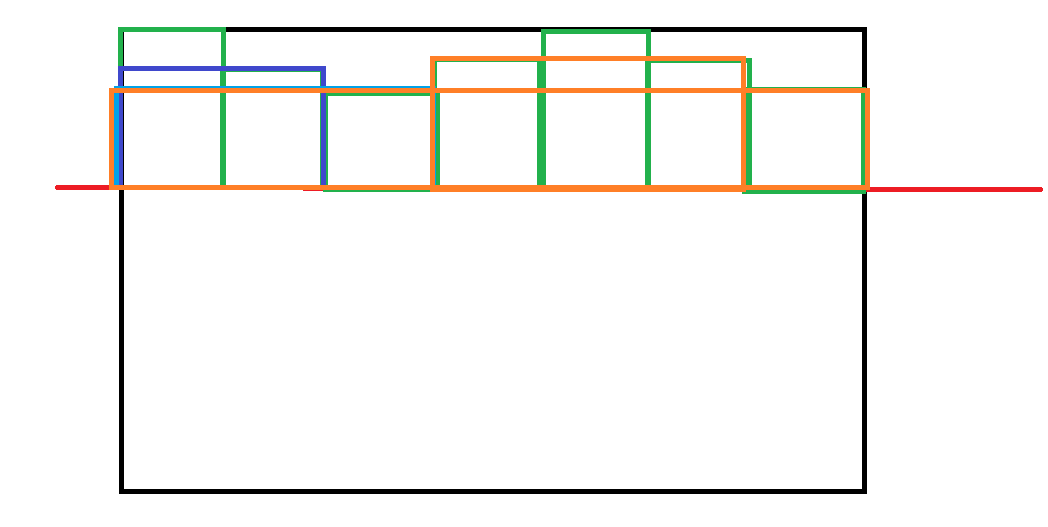
可以这样去取。

假设现在我们维护了一个这样的栈，右边是要加入的元素：

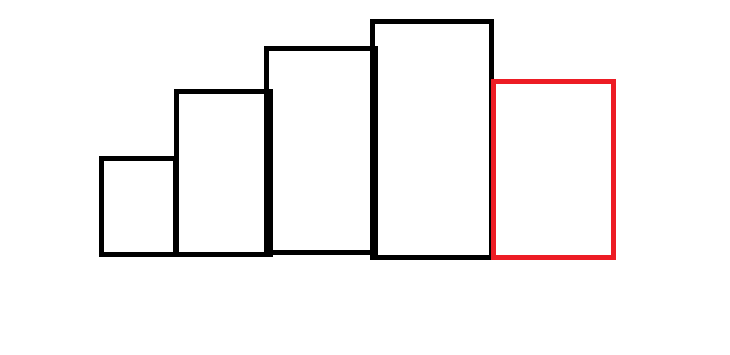
然后我们想把这个元素加入进去，在弹出元素的时候不断的去更新矩阵的面积。

因为栈顶的元素一定比他下面的元素要大，所以可以直接加上栈顶的宽度。

当维护完之后再加栈中的元素弹出，同时更新最大值。

/*
	Work by: TLE_Automation
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
#define int  long long
using namespace std;

const int N = 1e6 + 10;
const int MAXN = 2e5 + 10;

inline char readchar() {
	static char buf[100000], *p1 = buf, *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}

inline int read() {
#define readchar getchar
	int res = 0, f = 0;char ch = readchar();
	for(; !isdigit(ch); ch = readchar()) if(ch == '-') f = 1;
	for(; isdigit(ch); ch = readchar()) res = (res << 1) + (res << 3) + (ch ^ '0');
	return f ? -res : res;
}

inline void print(int x) {
	if (x < 0 ) putchar('-'), x = -x;
	if (x > 9 ) print(x / 10);
	putchar(x % 10 + '0');
}
int n, m, a[1004][1004], sc = 0;
char ch[1004][1004], s;
int ans = 0;

struct node {
	int high, wide;
}stc[N];

signed main() {
	n = read(), m = read();
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			cin >> s;
			if(s == 'R') a[i][j] = 0;
			else if(s == 'F') a[i][j] = a[i - 1][j] + 1;
		}
	}
	for(int k = 1; k <= n; k++) { // 枚举悬线
		int tmp = 0, maxx = 0;
		stc[++sc].high = a[k][1], stc[sc].wide = 1;
		for(int i = 2; i <= m; i++) {
			tmp = 0;
			while(stc[sc].high >= a[k][i] && sc) {
				tmp += stc[sc].wide;
				maxx = max(maxx, stc[sc].high * tmp);
				--sc;
			}
			stc[++sc].high = a[k][i], stc[sc].wide = tmp + 1;
		}
		tmp = 0;
		while(sc) {
			tmp += stc[sc].wide;
			maxx = max(maxx, tmp * stc[sc].high);
			--sc;
		}
		ans = max(ans, maxx);
	}
	return print(ans * 3), 0;
}