对角矩阵的压缩储存

带状矩阵的定义是对于n*n的方阵，若它的全部非零元素落在一个以主对角线为中心的带状区域中，这个带状区域包含主对角线， 以及主对角线下面及上面各b条对角线上的元素。

想要将对带状矩阵进行压缩，是有规则的二维数组中的非零元素进行排列，就是在i、j、d(为带状两边的非零元素的个数)、n之间找出规律和关系来，这其实就比较考验我们的找规律的能力了。

 

首先比较容易得出的是，在带状矩阵中非零元素的个数一共为n(2d+1)-(d+1)d，也就是整个压缩为一维数组的大小（将其左上和右下的三角分别补充再相减）。

 

我们将定义1<=i,j<=n，把它压缩的一维数组至下标为0~n(2d+1)-(d+1)d-1的一维数组当中。

一、k=1：

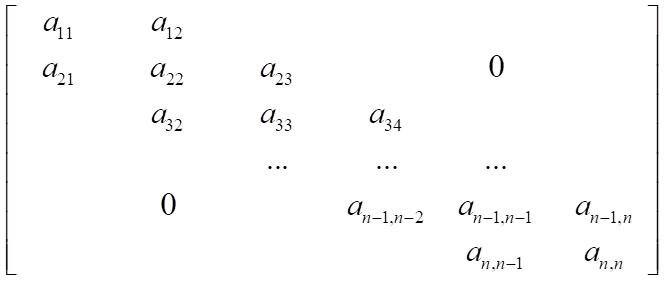
这是一种比较简单的情况，除了第一行和第n行以外，每一行的非零元素的个数都为3（即2*d+1），此时可用计算非零元素个数的方法计算出其对应压缩的下标：

k=（i-1)(2d+1)+j-i+d-1，把d=1带入，k=2i+j-3; （j-i+d为此元素在这一行的非零元素中的序号）

 

二、当带宽=d时（d<n/2，此时是在中间部分完整行为2d+1）：

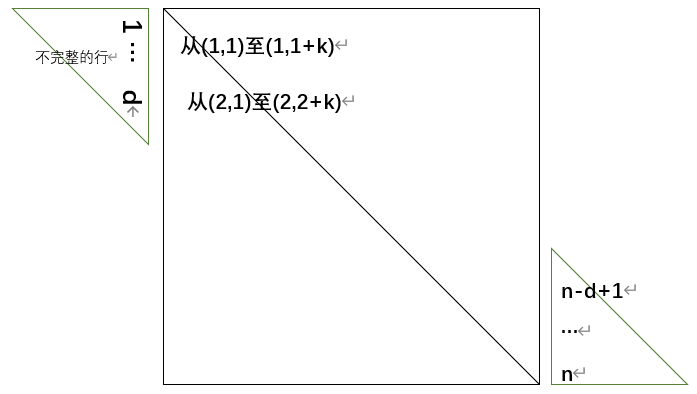
看到这个模型，我还不太知道怎么将其转换为一个通用的压缩公式，最直接的办法就是将其分类讨论，第一种时是不完整的行（i<=d）、第二种是不完整+完整（i<=n-d）、第三种是不完整+完整+不完整（i>n-d）

当i<=d时：k=（d+1+d+i-1)*(i-1)/2+j-i+d=(2d+i)*(i-1)/2+j-i+d;  【(d+1+d+i-1)*(i-1)/2为前i-1行非零元的个数，j-i+d为此元素在这一行的非零元素中的序号】

当i<=n-d时：k=(d+1)*d/2+(2d+1)*(i-d-1)+j-i+d; 【(d+1)*d/2为不完整行非零元个数和，(2d+1)*(i-d-1)为完整行的个数和，j-i+d为此元素在这一行的非零元素中的序号】

当i>n-d时：k=(d+1)*d/2+(2d+1)*(n-2d)+j-i+d+(i+4d-n)*(i+d-n)【和上面差不多，一直叠加计算，但这里的计算难倒我了，数学不太行，也有可能是我计算的方法太复杂了】

--暂无代码

 

三、当带宽=d时（d>n/2，没有完整行2d+1个非零元素）：

 

 

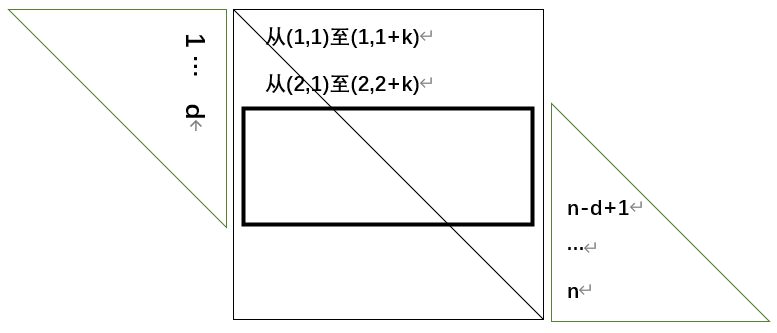
 这个情况和二的情况类似，粗体黑框的部分是没有达到完整的2d+1个非零元素，可能也是需要从中做出笨笨的分类。

但怎么从中找出其下标和一维数组的规律呢，还有待我做出数学计算，相信脑袋秃秃的你一定可以算的非常okk~

 

暂时还没有想到可以用一个公式来表达！！就算这样分类我也算的花里胡哨的！！感觉只有当带宽=1的时候是可以用一个公式进行总结的。有的并不是完整连续对应在0~n(2d+1)-(d+1)d-1的下标下的话，其实是有一种 i、j、k之间的哈希的感觉了。还有的就是压缩为i×(2d+1)的矩阵的，比较也比较方便的，但还是会有一定程度上的浪费吧。得转起脑子来 8868