实变函数，第四章，可测函数
第四章的知识地图
一，可测函数的性质
1，把无穷定义为实数，那么值域为实数和无穷的函数叫广义实值函数
2，函数有界就是有限函数，但是函数有限，并不一定有界
3，可测函数的定义：
定义在可测集E的函数，当f（x）>a时（a为有限实数），E的子集是可测集，那么f就是可测函数。（就是一叠硬币的数量大于某个值时，这个积分是可求的）
对于这个定义，有4个等价的充要替换条件：
a， f大于等于a，小于等于a，小于a可测
b，或在a，b之间都可测（f必须为有限函数，这个条件不是充分条件）
4，关于连续函数的定义：
当值域变化很小时，定义域也可以变化很小，在任意定义域内都有这个性质的函数，就是连续函数，用集合的语言就是，x0和y0的领域可以无穷小，且f（x0的领域）在y0领域之内
5，连续函数是可测函数
因为，当E(f>a)时，由于函数连续，他的定义域可以定义为无数领域的并，定义域E是可测，领域也可测，所以E和领域并的交集也可测
6,函数运算的可测性
- 函数的1/f是可测的
- 函数的和是可测的
- 函数的积是可测的
- 函数的商也是可测的
函数将值域反向映射到定义域，用数值的大小来映射，本质上是将定义域进行分割，只要分割出来的定义域是可测的，那么函数就是可测的，除非这个反向映射将原来的定义域分割成了不可测空间
7，函数列（可数）的上下确界是可测的
但是连续函数的上下确界未必连续
8，函数列的极限是可测的
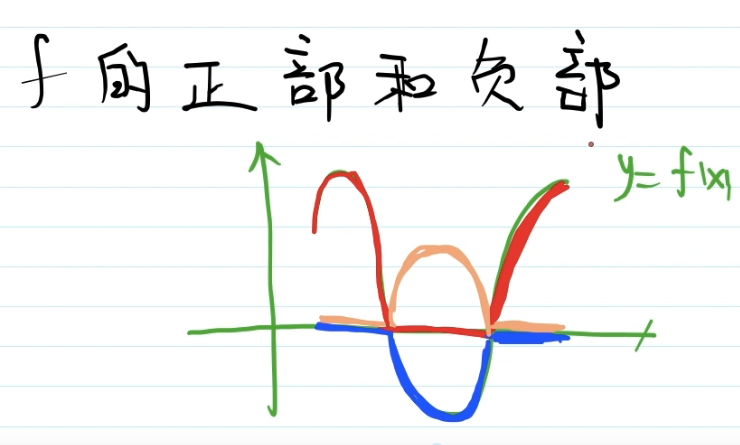
9，函数的正部分与负部
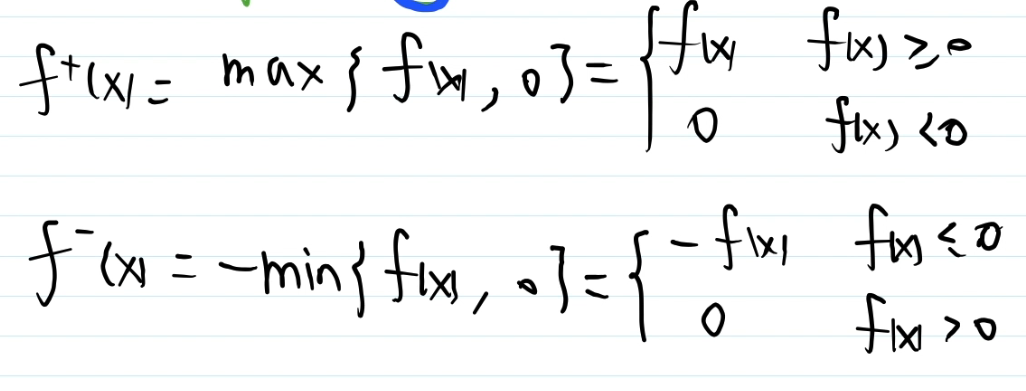
10，可测函数的举例
#连续函数和区间递增函数都是可测的
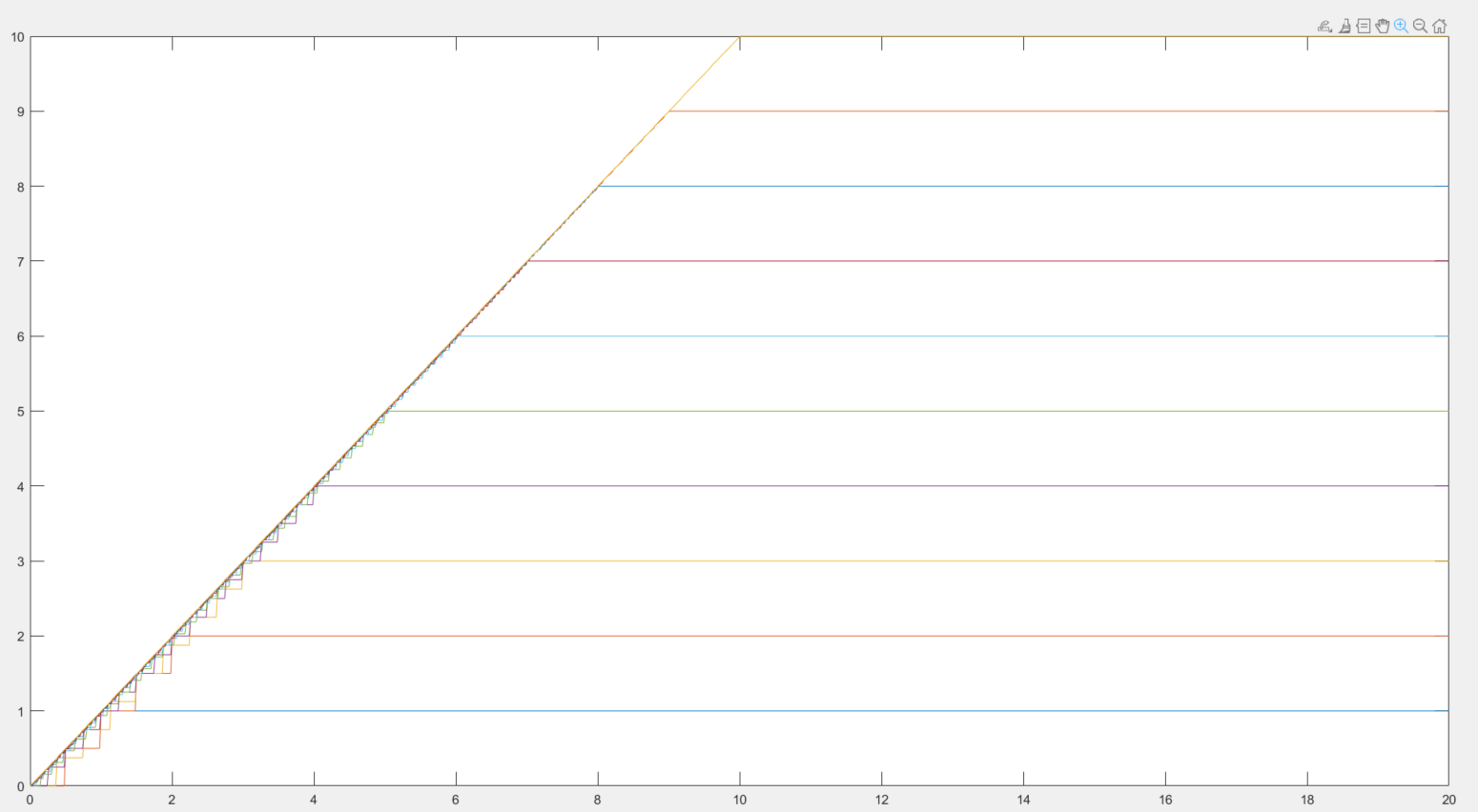
11，简单函数逼近可测函数
#matlab代码
% 用简单函数拟合可测函数
clear
x = linspace(0,20,1000); %x为横坐标
for k=1:10
for i=linspace(0,k,2^k+1)
f(k,(x>i))=i;
end
end
plot(x,f)
#代码结束
4阶简单函数
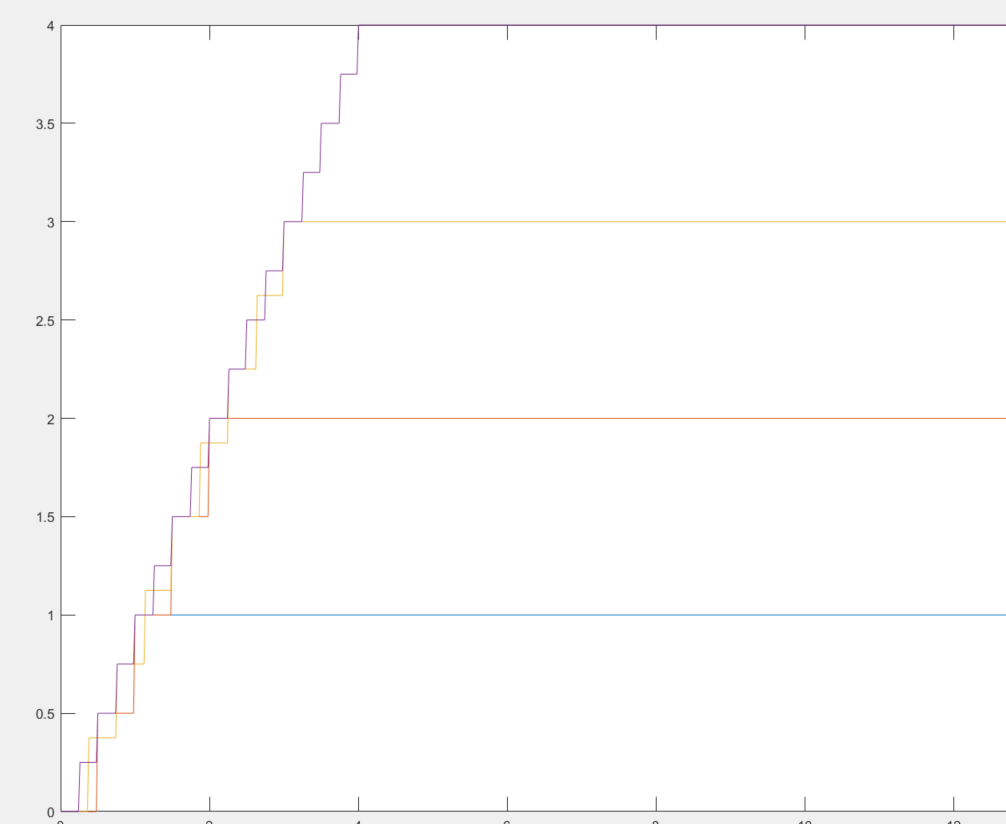
10阶简单函数
二，叶果罗夫定理
1，一致收敛的函数列，可以换序，可以收敛到连续函数，当所收敛的函数是可去间断点（去掉0测集的定义域）那么这个命题就是a，e成立
2，关于收敛函数，开始的时候我理解为二元函数，但是并不是，这是一个离散的二元函数，因为，他不是连续的
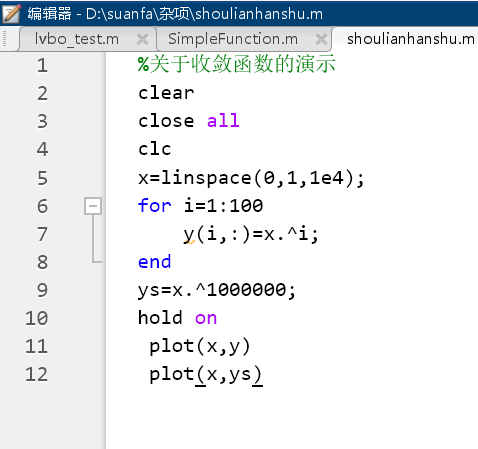
这个是离散函数
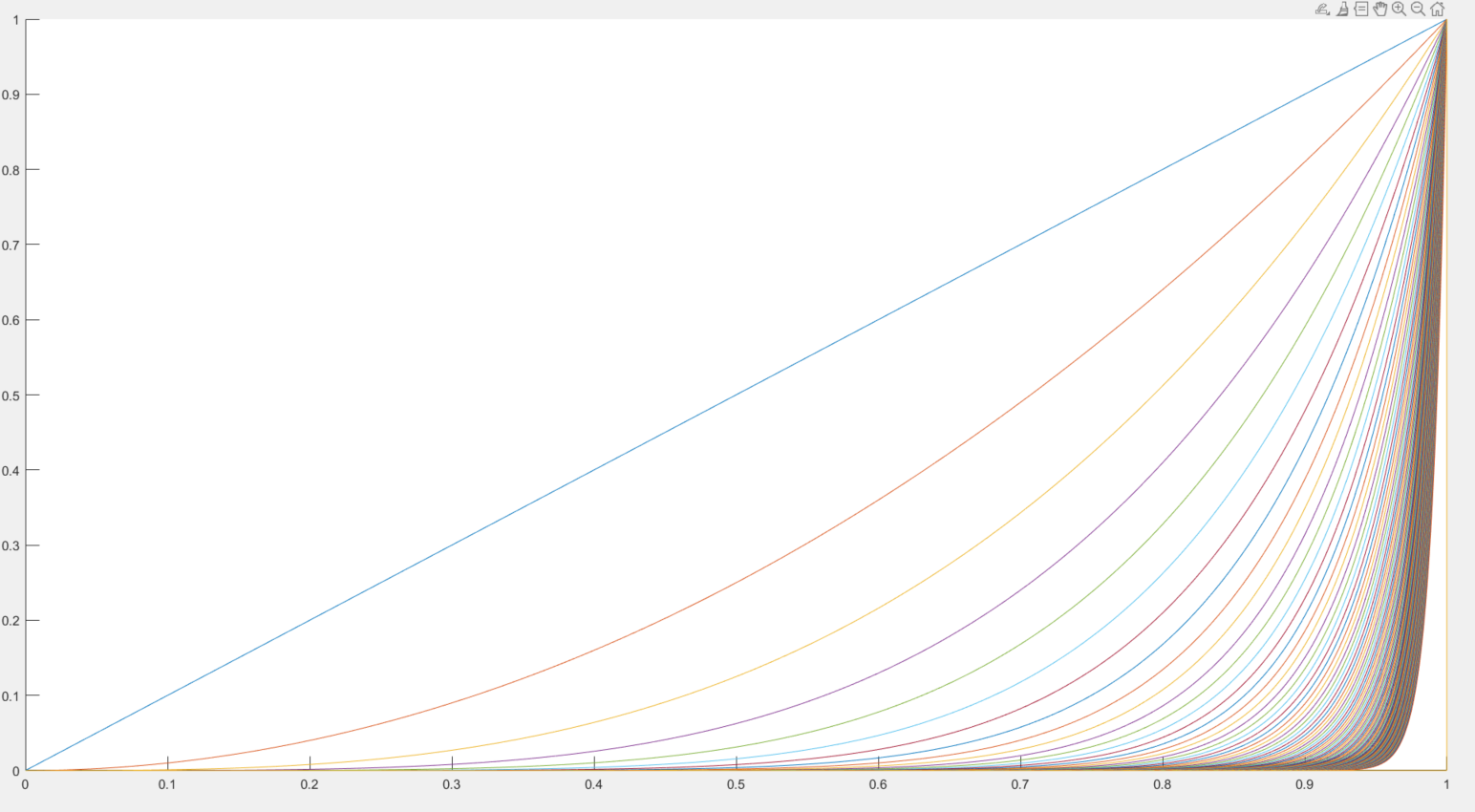
这个是连续函数，实际上并没有本质区别，还是一个二维函数
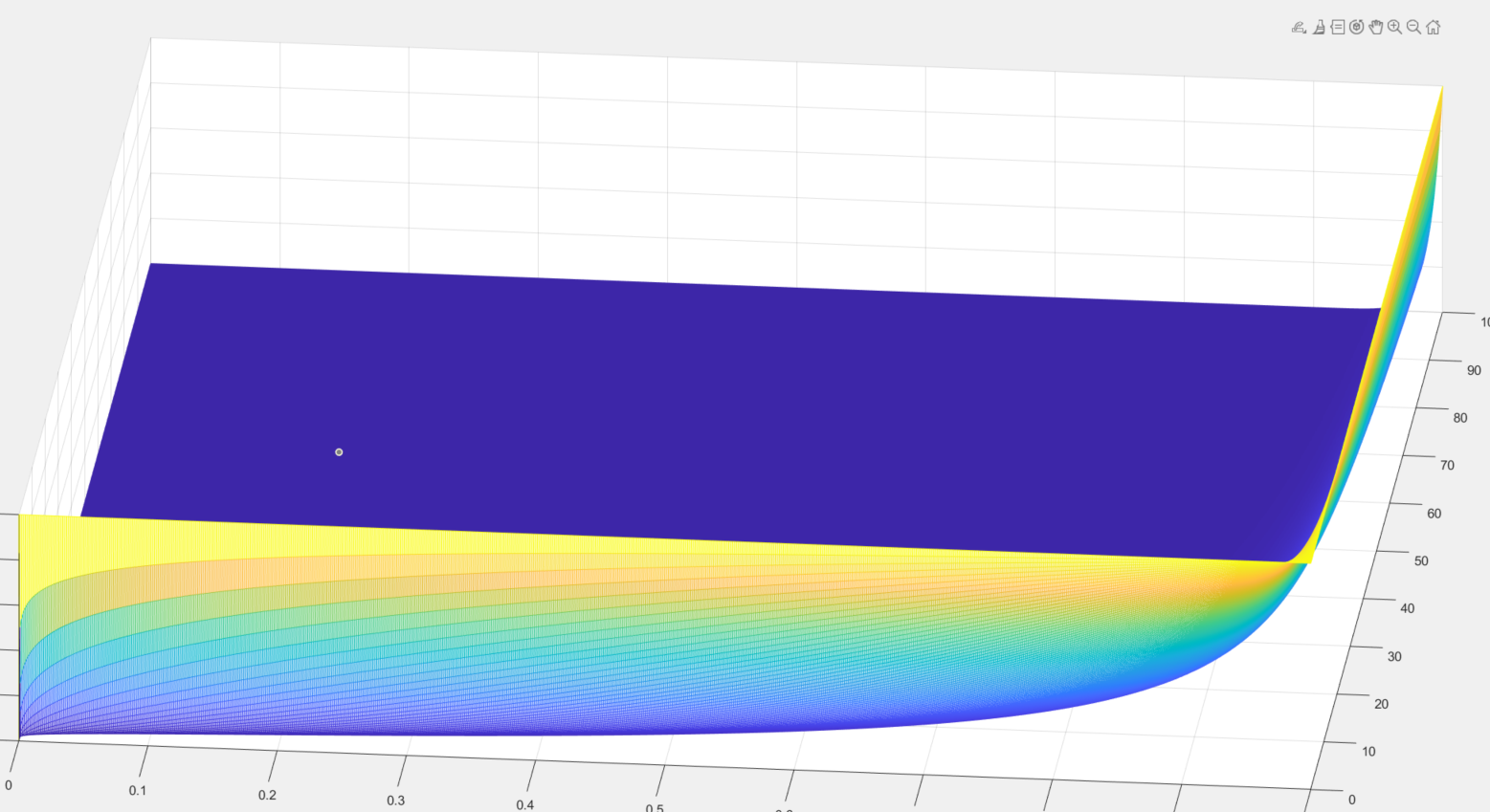
3，叶果罗夫定理：
大关节就是，逐点收敛，的可去o测集，就是和一致收敛相似，函数值应该是有限的
4，三种收敛方式：驻点收敛，几乎处处收敛，一致收敛，那么当n足够大的时候，测度为零的距离收敛，就是依测度收敛。
便宜某个收敛值的测度为0，就是依测度收敛（函数值是有限的，如果是无限的，那又不一样了，因为无限是个不确定的领域）
下面这个图，和函数f（x）=0就是依测度收敛，虽然fn和f不相等，但是他们不相等的定义域的测度是0
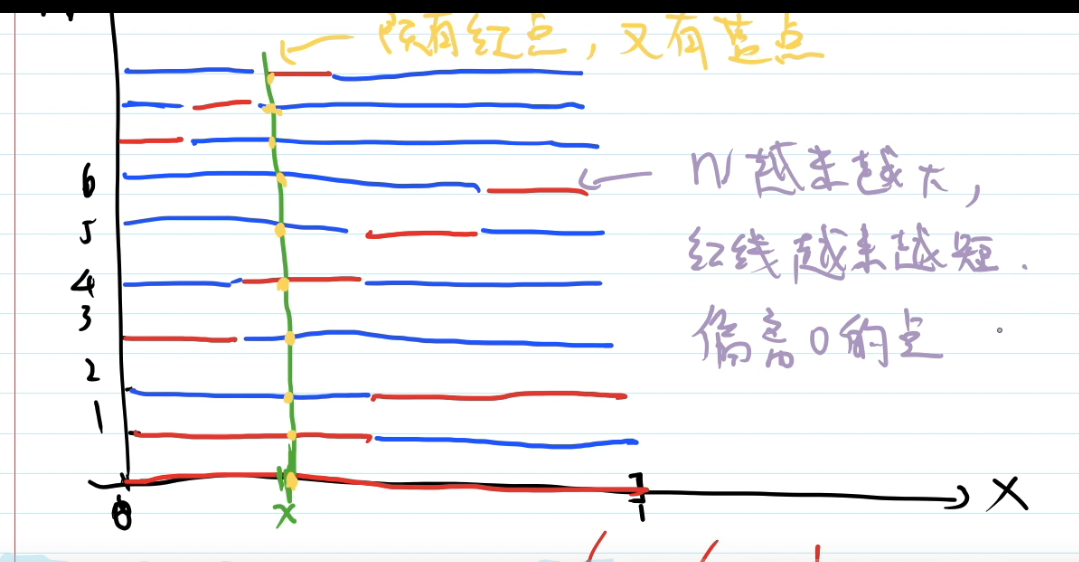
5，依测度收敛，不能推出逐点收敛和一致收敛
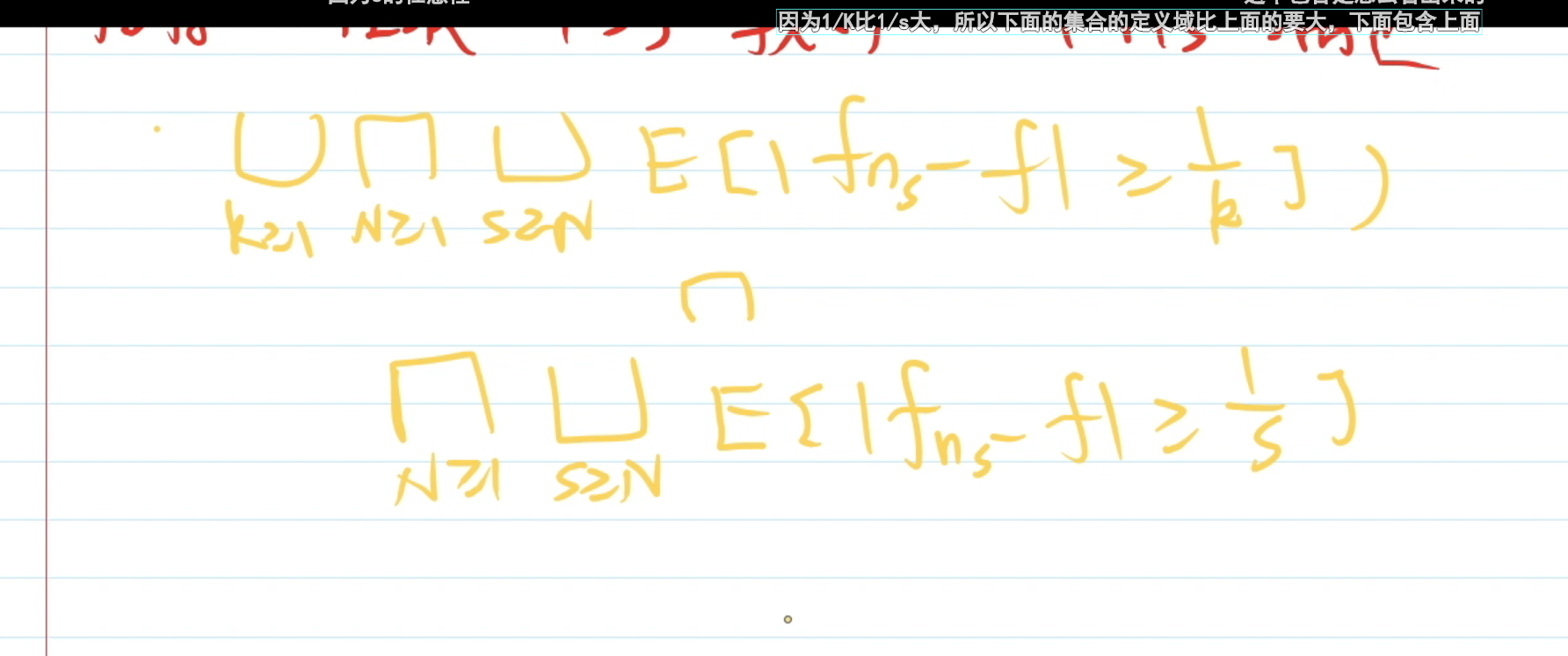
6，一列集合，函数f在每个集合上连续，那么在这些集合的并集也连续，即使看上去不连续，因为没有定义的地方是断开的，但是有定义的端点是左/右连续的
