分支限界法-01背包问题

1、分支限界法介绍

      分支限界法类似于回溯法，也是在问题的解空间上搜索问题解的算法。一般情况下，分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出解空间中满足约束条件的所有解；而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解，即在某种意义下的最优解。

      由于求解目标不同，导致分支限界法与回溯法对解空间的搜索方式也不相同。回溯法以深度优先的方式搜索解空间，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间。

      分支限界法的搜索策略是，在扩展结点处，先生成其所有的儿子结点(分支)，然后再从当前的活结点表中选择下一扩展结点。为了有效地选择下一扩展结点，加速搜索的进程，在每一个活结点处，计算一个函数值(限界)，并根据函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间上有最优解的分支推进，以便尽快地找出一个最优解。这种方式称为分支限界法。人们已经用分支限界法解决了大量离散最优化的问题。

2、常见的两种分支限界法

1. 队列式（FIFO）分支限界法：按照先进先出原则选取下一个节点为扩展节点。 活结点表是先进先出队列。

   LIFO分支限界法：活结点表是堆栈。

2. LC（least cost）分支限界法（优先队列式分支限界法）：按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。 活结点表是优先权队列，LC分支限界法将选取具有最高优先级的活结点出队列，成为新的E-结点。

     FIFO分支限界法搜索策略：

§一开始，根结点是唯一的活结点，根结点入队。

§从活结点队中取出根结点后，作为当前扩展结点。

§对当前扩展结点，先从左到右地产生它的所有儿子，用约束条件检查，把所有满足约束函数的儿子加入活结点队列中。

§再从活结点表中取出队首结点（队中最先进来的结点）为当前扩展结点，……，直到找到一个解或活结点队列为空为止。

     优先队列式分支限界法搜索策略：

§对每一活结点计算一个优先级（某些信息的函数值）；

§根据这些优先级从当前活结点表中优先选择一个优先级最高（最有利）的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进，以便尽快地找出一个最优解。

§再从活结点表中下一个优先级别最高的结点为当前扩展结点，……，直到找到一个解或活结点队列为空为止。

3、解决01背包问题算法的思想

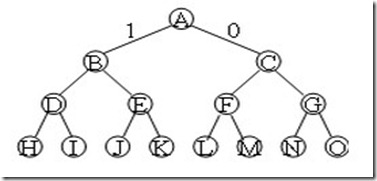
01背包问题状态空间树

• FIFO限界：若当前分支的“装载的价值上界”，比现有的最大装载的价值小，则该分支就无需继续搜索。

队列式分支法

队列式分支限界法

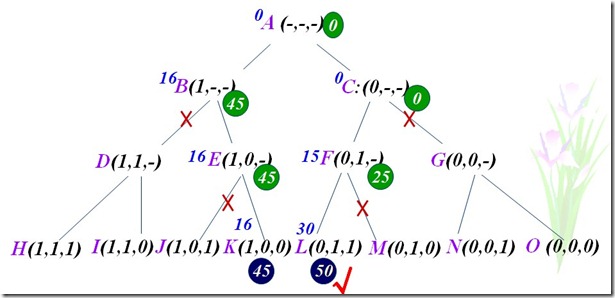
• 优先队列限界：优先队列搜索得到当前最优解作为一个“界”，对上界（或下界）不可能达到（大于）这个界的分支则不去进行搜索，这样就缩小搜索范围，提高了搜索效率。

优先队列式分支法

优先队列式分支限界法

      算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点，则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点，仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。

上界函数

// maxBound函数求最大上界
private double maxBound(int t) {
    double left = max - c_weight, b = c_value;
    // 剩余容量和价值上界
    while (t < n && weight[t] <= left)
    // 以物品单位重量价值递减装填剩余容量
    {
        left -= weight[t];
        b += value[t];
        t++;
    }
    if (t < n)
        b += value[t] / weight[t] * left;
    // 装填剩余容量装满背包
    return b;
}

分支限界算法 

int i = 0;
double upper = maxBound(i);
// 调用MaxBound求出价值上界，best为最优值
while (true)
// 非叶子结点
{
    double wt = c_weight + weight[i];
    if (wt <= max)
    // 左儿子结点为可行结点
    {
        if (c_value + value[i] > bestv)
            bestv = c_value + value[i];
        addLiveNode(upper, c_value + value[i], c_weight + weight[i],
                i + 1);
    }
    upper = maxBound(i + 1);
    if (upper >= bestv) // 右子数可能含最优解
        addLiveNode(upper, c_value, c_weight, i + 1);
    if (heap.empty())
        return bestv;
    HeapNode node = heap.peek();
    // 取下一扩展结点
    heap.pop();
    c_weight = node.weight;
    c_value = node.value;
    upper = node.upper;
    i = node.level;
}

4、算法实现

import java.util.Stack;

class HeapNode {
    double upbound; // 结点的价值上界
    double value; // 结点所对应的价值
    double weight; // 结点所相应的重量

    int level; // 活节点在子集树中所处的层序号

    public HeapNode() {
    }
}

// 分支限界法实现01背包问题
public class BB_Knapsack01 {

    int[] weight;
    int[] value;
    int max; // 背包的最大承重量

    int n;

    double c_weight; // 当前背包重量
    double c_value; // 当前背包价值

    double bestv; // 最优的背包价值

    Stack<HeapNode> heap;

    public BB_Knapsack01() {
        weight = new int[] { 15, 16, 15, 0 };
        value = new int[] { 25, 45, 25, 0 };
        max = 30;

        n = weight.length - 1;

        c_weight = 0;
        c_value = 0;
        bestv = 0;

        heap = new Stack<HeapNode>();
    }

    // 求子树的最大上界
    private double maxBound(int t) {
        double left = max - c_weight;
        double bound = c_value;
        // 剩余容量和价值上界
        while (t < n && weight[t] <= left) {
            left -= weight[t];
            bound += value[t];
            t++;
        }
        if (t < n)
            bound += (value[t] / weight[t]) * left; // 装填剩余容量装满背包
        return bound;
    }

    // 将一个新的活结点插入到子集树和最大堆heap中
    private void addLiveNode(double upper, double cvalue, double cweight,
            int level) {
        HeapNode node = new HeapNode();
        node.upbound = upper;
        node.value = cvalue;
        node.weight = cweight;
        node.level = level;
        if (level <= n)
            heap.push(node);
    }

    // 利用分支限界法，返回最大价值bestv
    private double knapsack() {
        int i = 0;
        double upbound = maxBound(i);
        // 调用maxBound求出价值上界，bestv为最优值
        while (true) // 非叶子结点
        {
            double wt = c_weight + weight[i];
            if (wt <= max)// 左儿子结点为可行结点
            {
                if (c_value + value[i] > bestv)
                    bestv = c_value + value[i];
                addLiveNode(upbound, c_value + value[i], c_weight + weight[i],
                        i + 1);
            }
            upbound = maxBound(i + 1);
            if (upbound >= bestv) // 右子树可能含最优解
                addLiveNode(upbound, c_value, c_weight, i + 1);
            if (heap.empty())
                return bestv;
            HeapNode node = heap.peek();
            // 取下一扩展结点
            heap.pop();
            //System.out.println(node.value + " ");
            c_weight = node.weight;
            c_value = node.value;
            upbound = node.upbound;
            i = node.level;
        }
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        BB_Knapsack01 knap = new BB_Knapsack01();
        double opt_value = knap.knapsack();
        System.out.println(opt_value);
    }
}