约瑟夫环的五种解法(一行代码搞定)
**约瑟夫环问题**
约瑟夫环(约瑟夫问题,又作杀人游戏问题)是一个数学的应用问题:已知n个人(以编号1,2,3…n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。通常解决这类问题时我们把编号从0~n-1,最后 [1] 结果+1即为原问题的解。
问题来源:瑟夫环(Josephus)问题是由古罗马的史学家约瑟夫(Josephus)提出的,他参加并记录了公元66—70年犹太人反抗罗马的起义。约瑟夫作为一个将军,设法守住了裘达伯特城达47天之久,在城市沦陷之后,他和40名死硬的将士在附近的一个洞穴中避难。在那里,这些叛乱者表决说“要投降毋宁死”。于是,约瑟夫建议每个人轮流杀死他旁边的人,而这个顺序是由抽签决定的。约瑟夫有预谋地抓到了最后一签,并且,作为洞穴中的两个幸存者之一,他说服了他原先的牺牲品一起投降了罗马。
约瑟夫环问题的具体描述是:设有编号为1,2,……,n的n(n>0)个人围成一个圈,从第1个人开始报数,报到m时停止报数,报m的人出圈,再从他的下一个人起重新报数,报到m时停止报数,报m的出圈,……,如此下去,直到只剩下一个人为止
下面我们来解决这个问题,我们先建立约瑟夫环的一个模型,如下图所示:
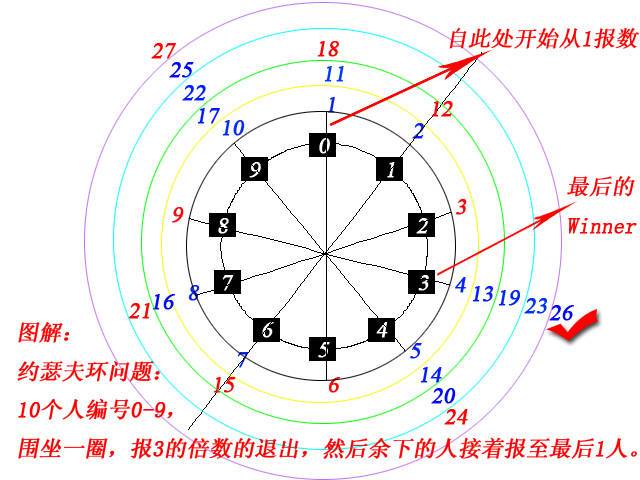
方法一:用C语言中的数组解决。
我们可以举个例子:例如a[100]={1,2,3,4,5,6},即n=6,这里假设m=3。我们将数组开辟的比n大是为了方便在数组后面添加元素,这里如果为了方便用vector容器也可。
设置一个变量count=1,用来计数从[1,m]。
从前往后遍历数组:当count!=3的时候a[n++]=a[i],
当count=3的时候重新令count=1;
数组元素的变化
-
1,2,3,4,5,6 -
1,2,3,4,5,6,1,2 -
1,2,3,4,5,6,1,2,4,5 -
1,2,3,4,5,6,1,2,4,5,1,2 -
1,2,3,4,5,6,1,2,4,5,1,2,5 -
1,2,3,4,5,6,1,2,4,5,1,2,5,1,2 -
1,2,3,4,5,6,1,2,4,5,1,2,5,1,2,1,2 -
1,2,3,4,5,6,1,2,4,5,1,2,5,1,2,1,2,2
到了临界条件即当前遍历的a[i]=a[i-1]的时候,打破循环,输出a[i]即是我们要求的最后一个人。
附上代码:
#include<stdio.h>
int main ()
{
int i,n,m,count=1;
int a[1000]={0};
scanf("%d %d",&n,&m);
for(i=0;i<n;i++)
a[i]=i+1;
for(i=0;i<n;i++)
{
if(count==m){
count=1;
}
else{
a[n]=a[i];
n++;
count++;
if(a[i]==a[i-1]){
printf("%d",a[i]);
break;
}
}
}
}
方法二:用一个队列轻松解决,将报数不为m(即count=m)的元素全部加到队尾,并删除当前元素。当遇到报数为m的元素,删除元素并令count=1 。
优于法一。
附上代码:
#include<stdio.h>
#include<queue>
using namespace std;
int main ()
{
queue<int>q;
int n,i,m,count=1;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
q.push(i);
while(!q.empty()){
if(q.size()==1){
printf("%d",q.front());
break;
}
else if(count==m){
q.pop();
count=1;
}
else{
count++;
q.push(q.front());
q.pop();
}
}
}
方法三:循环链表 最简单的一种不作多述。要点在于删除count=m时的结点不能直接删除。需找到此结点前的一个结点再作操作。
附上代码:
# include<stdio.h>
# include<stdlib.h>
struct node{
int data;
node*next;
}a[1000];
int main ()
{
void del(node* p);
int n,m,i;
int count=1,size;
scanf("%d %d",&n,&m); //输入n,m
size=n;
a[n-1].data=n;
a[n-1].next=&a[0];
for(i=0;i<n-1;i++)
{
a[i].data=i+1;
a[i].next=&a[i+1];
} //初始化链表
node*p=a;
while(size>0){
if(size==1) {
printf("%d",p->data); //当人数只有一个人的时候,输出该人的编号
break;
}
if(count==m-1){ //因为无法对count=m时候的结点直接修改,所以找到该结点前的一个结点
del(p);
count=1;
size--;
p=p->next;
}
else{
p=p->next;
count++;
}
}
}
void del(node* p){ //定义一个删除当前结点的下一个结点的函数
p->next=p->next->next;
}
方法四:
递归
n个人,数到m的出队。
假设用编号0,1,2,3,....,n-1来表示n个人的编号
0,1,2,3,..,m-2,m-1,m,...,n那么此时出队人的编号为(m-1)%n
删除前编号为m的元素现在则为0
则可得出递归条件:old=(new+m)%n
当队列中只有一个人的时候其编号就为0,这个就是递归的边界条件,最后需将编号加上1.
附上代码:
# include<stdio.h>
int main ()
{
int f(int n,int m);
int n,m,a;
scanf("%d %d",&n,&m);
a=f(n,m)+1;
printf("%d",a);
return 0;
}
int f(int n,int m){
return n==0?n:(f(n-1,m)+m)%n;
}
方法五:类似于递归的数学表示过程,一重循环。可以抽象为递推,从当人为2的时候反向递推,可以看作递归的逆过程,原理同方法四。
附上代码:
#include <stdio.h>
int main()
{
int n, m, i, a=0;
scanf("%d %d", &n, &m);
for(i=2;i<=n;i++)
{
a=(a+m)%i;
}
printf ("%d", a+1);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号