公式定理

目录

• 公式
  • 两个重要极限公式
  • 三角函数的全名
  • 导数公式
  • 等价无穷小公式
  • 麦克劳林级数
  • 傅里叶级数
    • 傅里叶级数
    • 傅里叶系数
    • 正弦级数
    • 余弦级数
  • 其他常用公式
• 定理
  • 罗尔定理
  • 拉格朗日定理
  • 柯西定理
  • 幂级数--阿贝尔定理的证明

公式

两个重要极限公式

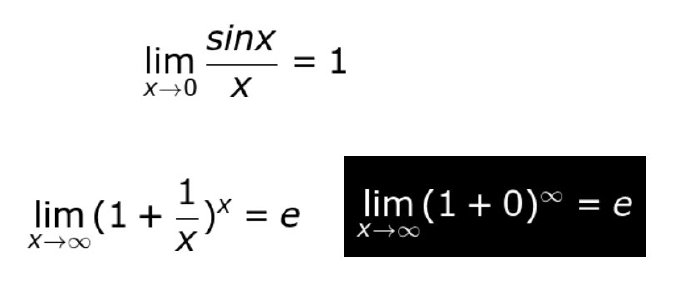
三角函数的全名

• 正弦：sine（简写sin）[sain]
• 余弦：cosine（简写cos）[kusain]
• 正切：tangent（简写tan）['tndnt]
• 余切：cotangent（简写cot）['ku'tndnt]
  \(\cot x=\frac{1}{\tan x}\)
• 正割：secant（简写sec）['si:knt]
  \(\sec x=\frac{1}{\cos x}\)
• 余割：cosecant（简写csc）['kau'si:knt]
  \(\csc x=\frac{1}{\sin x}\)
• 正矢：versine（简写versin）['v:sain]
• 余矢：versed cosine（简写vercos）['v:s:d][kusain]

---

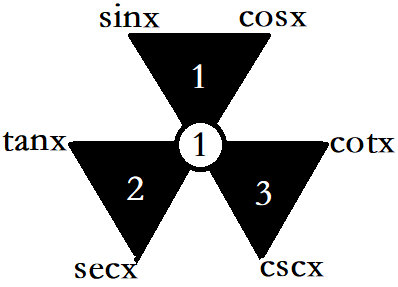
三个倒三角，两上角平方和等于下角平方。
\(\sin ^{2}x+\cos ^{2}x=1\)
\(\tan ^{2}x+1=\sec ^{2}x\)
\(1+\cot ^{2}x=\csc ^{2}x\)

---

导数公式

\((\log_{a}x)'=\frac{1}{x\ln a}(a>0,a\neq 1)\)

\((\tan x)'=\sec ^{2}x\)
\((\cot x)'=-\csc ^{2}x\)

\((\sec x)'=\sec x\tan x\)
\((\csc x)'=-\csc x\cot x\)

\((\arcsin x)'=\frac{1}{\sqrt{1-x^{2}}}\)
\((\arccos x)'=\frac{-1}{\sqrt{1-x^{2}}}\)

\((\arctan x)'=\frac{1}{1+x^{2}}\)
\((\textrm{arccot} x)'=\frac{-1}{1+x^{2}}\)

等价无穷小公式

当\(x\to 0\)时：

• \(\ln (1+x)=x-\frac{1}{2}x^{2}+\frac{1}{3}x^{3}+O(x^{3})\)
• \(\sin x=x-\frac{1}{6}x^{3}+O(x^{3})\)
• \(\cos x=1-\frac{1}{2}x^{2}+\frac{1}{24}x^{4}+O(x^{3})\)
• \(\arcsin x=x+\frac{1}{6}x^{3}+O(x^{3})\)
• \(\tan x= x+\frac{1}{3}x^{3}+O(x^{3})\)
• \(\arctan x= x-\frac{1}{3}x^{3}+O(x^{3})\)
• \(\ln (1+x)=x-\frac{1}{2}x^{2}+\frac{1}{3}x^{3}+O(x^{3})\)
• \(e^{x} = 1+x+\frac{1}{2}x^{2}+\frac{1}{6}x^{3}+O(x^{3})\)
• \((1+x)^{\alpha }=1+\alpha x+\frac{\alpha (\alpha -1)}{2}x^{2}+O(x^{2})\)

麦克劳林级数

【麦克劳林级数是函数在x=0处的泰勒级数】如果函数f(x)在点x=0处存在任意阶导数，则称\(f(0)+f'(0)x+\frac{f''(0)}{2!}x^{2}+\cdots +\frac{f^{(n)}(0)}{n!}x^{n}+\cdots\)为函数f(x)的麦克劳林公式，记作：$$f(x)\sim \sum_{n=0}^{\infty }\frac{f^{{(n)}(0)}{n!}x}$$
七个常见麦克劳林级数如下：

\[e^{x}=\sum_{n=0}^{\infty }\frac{x^{n}}{n!}=1+x+\frac{x^{2}}{2!}+\cdots +\frac{x^{n}}{n!}+\cdots ，-\infty <x<+\infty \]

\[\frac{1}{1+x}=\sum_{n=0}^{\infty }(-1)^{n}x^{n}=1-x+x^{2}-\cdots +(-1)^{n}x^{n}+\cdots ，-1<x<1 \]

\[\frac{1}{1-x}=\sum_{n=0}^{\infty }x^{n}=1+x+x^{2}+\cdots +x^{n}+\cdots ,-1<x<1 \]

\[\ln (1+x)=\sum_{n=1}^{\infty }(-1)^{n-1}\frac{x^{n}}{n}=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+\cdots +(-1)^{n-1}\frac{x^{n}}{n}+\cdots ,-1<x\leqslant 1 \]

\[\sin x=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+\cdots ,-\infty<x<+\infty \]

\[\cos x=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n}}{(2n)!}=1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots +(-1)^{n}\frac{x^{2n}}{(2n)!}+\cdots ,-\infty<x<+\infty \]

\[(1+x)^{a}=1+ax+\frac{a(a-1)}{2!}x^{2}+\cdots +\frac{a(a-1)\cdots (a-n+1)}{n!}x^{n}+\cdots ,\left\{\begin{matrix}x\in (-1,1),当a\leqslant -1,\\ x\in (-1,1],当-1<a<0,\\ x\in [-1,1],当a>0\end{matrix}\right. \]

其他麦克劳林级数：

\[\frac{1}{1+x^{2}}=\sum_{n=1}^{\infty}(-1)^{n-1}x^{2(n-1)}=1-x^{2}+x^{4}-x^{6}+\cdots +(-1)^{n-1}x^{2(n-1)},-1<x<1 \]

\[\arctan x=\sum_{n=1}^{\infty}(-1)^{n-1}\frac{x^{2n-1}}{2n-1}=x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-\frac{x^{7}}{7}+\cdots +(-1)^{n-1}\frac{x^{2n-1}}{2n-1},-1<x<1 \]

令x=1，则$$\frac{\pi }{4}=\arctan 1=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots +(-1)^{n-1}\frac{1}{2n-1}$$

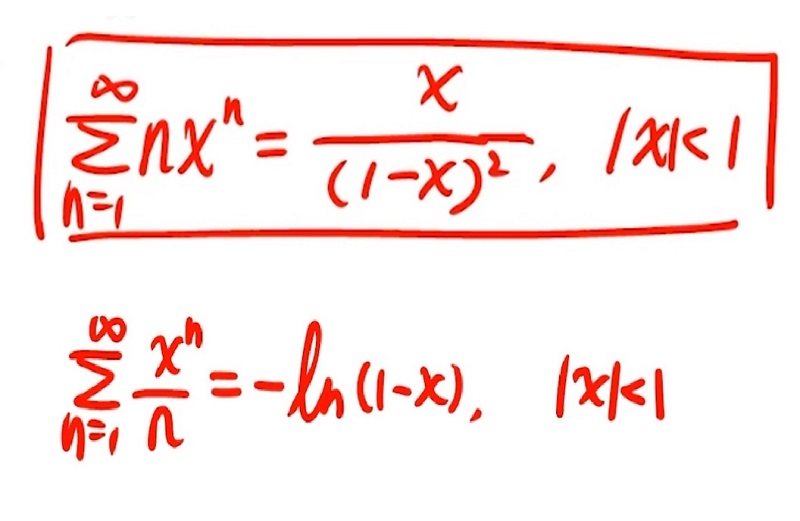
傅里叶级数

傅里叶级数

设f(x)是定义在\((-\infty,+\infty)\)内的周期为2\(\pi\)的函数，且能展开成三角级数，即傅里叶级数：

\[f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}(a_{n}\cos nx+b_{n}\sin nx) \]

傅里叶系数

这里由f(x)确定的系数\(a_{0},a_{1},\cdots,a_{n};b_{0},b_{1},\cdots,b_{n},\)叫做函数f(x)的傅里叶系数

\(a_{0}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx\)
$a_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx,n=1,2,\cdots \( \)b_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx,n=1,2,\cdots $

正弦级数

当f(x)为奇函数时，
$a_{n}=0,n=0,1,2,\cdots \( \)b_{n}=\frac{2}{\pi}\int_{0}^{\pi}f(x)\sin nxdx,n=1,2,\cdots $
此时傅里叶级数变成只含有正弦项的正弦级数：

\[f(x)=\sum_{n=1}^{\infty}b_{n}\sin nx \]

余弦级数

当f(x)为偶函数时，
\(a_{n}=\frac{2}{\pi}\int_{0}^{\pi}f(x)\cos nxdx,n=0,1,2,\cdots\)
$b_{n}=0,n=0,1,2,\cdots $
此时傅里叶级数变成只含有常数项和余弦项的余弦级数：

\[f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos nx \]

其他常用公式

• 两数和的幂的展开式
  • \((E+B)^{n} =E^{n}+nE^{n-1}B+\frac{n(n-1)}{2!}E^{n-2}B^{2}+\frac{n(n-1)(n-2)}{3!}E^{n-3}B^{3}+...+B^{n}\)

\[=\sum_{k=0}^{n}C_{n}^{k}E^{n-k}B^{k} \]

• 差化积
  • \(x^{n}-1 = (x-1)(x^{n-1}+x^{n-2}+...+x+1)\)
  • \(a^{3}-b^{3} = (a-b)(a^{2}+ab+b^{2})\)

定理

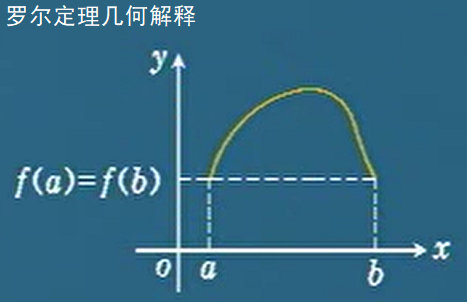
罗尔定理

若f(x)有：
1、在[a,b]上连续
2、在(a,b)上可导
3、f(a)=f(b)

那么，存在\(\xi \in (a,b)，使f'(\xi )=0\)

拉格朗日定理

若f(x)有：
1、在[a,b]上连续
2、在(a,b)上可导

那么，存在\(\xi \in (a,b)，使f '(ξ)=\frac{f(b)-f(a)}{b-a}\)
或写成：
1、\(f(b)-f(a)=f'(\xi )(b-a)\)
2、\(f(x)=f(a)+f'(\xi )(x-a)\)
3、\(f(x)=f(a)+\int_{a}^{x}f'(t)dt\)

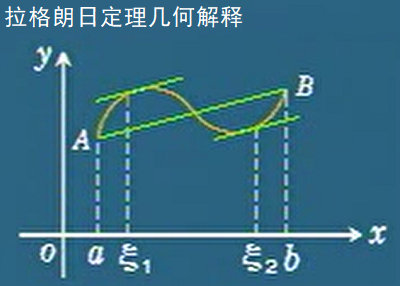
注：若f(a)=f(b)且a\(\neq\)b，那么拉格朗日定理变成罗尔定理，即罗尔定理是拉格朗日定理的一种特殊情况。

柯西定理

若f(x)，g(x)有：
1、在[a,b]上连续
2、在(a,b)上可导
3、\(g'(x)\neq 0\)

那么，存在ξ∈(a,b)，使\(\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(\xi )}{g'(\xi )}\)

注：若g(x)=x，则柯西定理变成拉格朗日定理。

幂级数--阿贝尔定理的证明

\[R=\lim_{n\to \infty}\left | \frac{a_{n}}{a_{n+1}} \right | \]

根据比值审敛法，有：$$p=\lim_{n\to \infty}\left | \frac{a_{n+1}x^{{n+1}}{a_{n}x}{n}} \right |=\lim_{n\to \infty}\left | \frac{a_{n+1}}{a_{n}} \right ||x|=\frac{|x|}{R}<1$$
故：|x|<R时级数收敛，|x|>R时级数发散