学习笔记:tarjan
tarjan
引入
Robert Tarjan,计算机科学家,以 LCA、强连通分量等算法而闻名。Tarjan 设计了求解的应用领域的广泛有效的算法和数据结构。他以在数据结构和图论上的开创性工作而闻名,他的一些著名的算法有 Tarjan 最近公共祖先离线算法,Tarjan 的强连通分量算法以及 Link-Cut-Trees 算法等。其中 Hopcroft-Tarjan 平面嵌入算法是第一个线性时间平面算法。Tarjan 也开创了重要的数据结构如:斐波那契堆和 splay 树,另一项重大贡献是分析了并查集。他是第一个证明了计算反阿克曼函数的乐观时间复杂度的科学家。
Tarjan 算法,又称为 Tarjan’s algorithm,是一个用于求解图的强连通分量(Strongly Connected Component)的算法。它是由美国计算机科学家 Robert Tarjan 在 1972 年提出的。(然而实际上能求的不只有强连通分量?)
前置知识
栈
栈是 OI 中常用的一种线性数据结构,其修改是按照后进先出的原则进行的,因此栈通常被称为是后进先出(last in first out)表,简称 LIFO 表。
可以考虑用数组模拟一个栈,定义一个变量 top 表示栈顶指针。
int stk[100005], top = 0; // 定义一个大小为 100005 的栈,初始时将指针指向栈底(即 0)
void insert(int x){ // 插入一个元素到栈顶
top++;stk[top] = x;
}
void remove(int x){ // 删除栈顶元素
top--;
}
int size(){ // 读取栈大小(即栈内元素个数)
return top;
}
void clear(){ // 清空栈
top = 0;
}
int top(){ // 读取栈顶元素
return stk[top];
}
STL stack
简介
栈是一种先进后出的容器。
头文件
#include <stack>
初始化
stack <int> s;
stack <string> s;
stack <node> s; //node 是结构体类型
函数
| 函数 | 含义 |
|---|---|
push(x) |
将 \(x\) 入栈 \(O(1)\) |
pop() |
将栈顶元素出栈 \(O(1)\) |
top() |
返回栈顶元素 \(O(1)\) |
empty() |
检测栈是否为空 \(O(1)\) |
size() |
返回元素个数 \(O(1)\) |
访问
STL 中的栈仅支持读取栈顶元素,如果需要遍历则需要将所有元素出栈。
可以考虑用数组模拟栈,比 STL 的 stack 容器速度更快,且遍历元素更加方便。
STL vector
简介
vector 一词在英文中是向量的意思。
vector 为可变长数组(即动态数组),可以随时添加数值和删除数值。
注意
在局部区域中开 vector 是在堆空间开的
在局部区域开数组是在栈空间开的,而栈空间比较小,如果开了很大的数组就会爆栈。
所以,在局部区域中不能开大数组,但能开大 vector。
头文件
#include <vector>
初始化
vector <int> a; // 定义了一个名为 a 的一维数组,数组存储 int 类型数据
vector <double> b;// 定义了一个名为 b 的一维数组,数组存储 double 类型数据
vector <node> c;// 定义了一个名为 c 的一维数组,数组存储结构体类型数据,node 是结构体类型
vector <int> v(n);// 定义一个长度为 n 的数组,初始值默认为 0,下标范围[0, n - 1]
vector <int> v(n, 1);// v[0] 到 v[n - 1] 所有的元素初始值均为 1
//注意:指定数组长度之后(指定长度后的数组就相当于正常的数组了)
vector <int> a{1, 2, 3, 4, 5};//数组 a 中有五个元素,数组长度就为 5
vector <int> a(n + 1, 0);
vector <int> b(a);// 两个数组中的类型必须相同,a 和 b 都是长度为 n + 1,初始值都为 0 的数组
vector <int> v[5];// 定义可变长二维数组
// 注意:行不可变(只有 5 行), 而列可变,可以在指定行添加元素
// 第一维固定长度为 5,第二维长度可以改变
vector <vecto <int>> v;//定义一个行和列均可变的二维数组
函数
| 函数 | 含义 |
|---|---|
front() |
返回第一个数据 \(O(1)\) |
pop_back() |
删除最后一个数据 \(O(1)\) |
push_back(x) |
在尾部加一个数据 \(O(1)\) |
size() |
返回数据个数 \(O(1)\) |
clear() |
清空容器 \(O(n)\) |
resize(x, y) |
将数组大小改为 \(x\),\(x\) 个空间赋值为 \(y\),没有 \(y\) 默认为 \(0\) |
insert(x, y) |
向迭代器 \(x\) 中插入一个数据 \(y\) \(O(n)\) |
erase(x, y) |
删除 \([x, y)\) 中的所有数据 \(O(n)\) |
begin() |
返回首元素迭代器 \(O(1)\) |
end() |
返回末元素后一个位置的迭代器 \(O(1)\) |
empty() |
判断容器是否为空 \(O(1)\) |
访问
可以直接和数组一样访问。
vector <int> a;
a.push_back(1);
cout << a[0] << endl;
也可以采用迭代器访问。
vector <int> a;
a.push_back(1);
vector <int>::iterator tmp = a.begin();
cout << *tmp << endl;
for(tmp = a.begin() ; tmp != a.end() ; tmp ++)
cout << *tmp << endl;
也可以使用智能指针,但只能一次性遍历完整个数组。
vector <int> v;
v.push_back(114514);
v.push_back(1919810);
for(auto val : v)
cout << val << " "; // 114514 1919810
一些概念
割点和割边
割点:在一个无向连通图 \(G=(V,E)\) 中,若存在一个点 \(x \in V\) 使得从图中删去这个点以及与这个点相连的所有边后整个图不再连通,则这个点是割点。
割边(或者叫做桥):在一个无向连通图 \(G=(V,E)\) 中,若存在一条边 \(x \in E\) 使得从图中删去这条边后整个图不再连通,则这条边是割边。
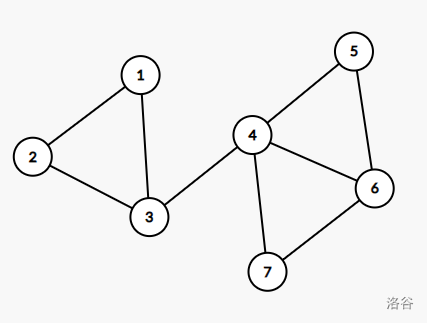
在上图中,观察可知,\(3\)、\(4\) 是割点,边 \((3,4)\) 是割边。
时间戳
在图的深度优先遍历过程中,按照每个节点第一次被访问的时间顺序,依次给予 \(n\) 个节点 \(1\) 到 \(n\) 的整数标记,该标记就被称为”时间戳“,记为 dfn[x]。
搜索树
在无向连通图中任选一个节点出发进行深度优先遍历,每个点只访问一次。所有发生递归的边 \((x,y)\)(换言之,从 \(x\) 到 \(y\) 是对 \(y\) 的第一次访问)构成一棵树,我们把它称为“无向连通图的搜索树”。当然,一般无向图(不一定连通)的各个连通块的搜索树构成无向图的“搜索森林”。这棵树上的边称作树边,不在树上的边称作非树边。
下图显然是上图构成的一棵搜索树。
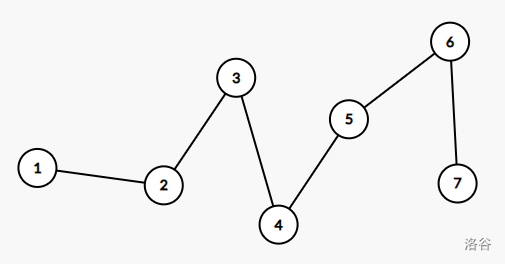
当然,搜索树一般情况下可能会有多个,这里只给出其中一种。
追溯值
令 son[x] 表示以 \(x\) 为根的子树,则追溯值 low[x] 定义为以下节点的时间戳的最小值:
son[x]中的节点。- 通过一条不再搜索树上的边能够到达
son[x]的节点。
以上图为例。为了叙述简便,我们用时间戳代替节点编号。son[4] = {4,5,6,7}。另外,节点 \(6\) 通过不在搜索树上的边 \((4,6)\) 能够到达 。所以 low[6] = 4。
根据定义,为了计算low[x],应该先令 low[x] = dfn[x],然后考虑从 \(x\) 出发的每条边 \((x,y)\):
-
若在搜索树上 \(x\) 是 \(y\) 的父节点,则令
low[x] = min(low[x], low[y])。 -
若无向边 \((x,y)\) 不是搜索树上的边,则令
low[x] = min(low[x], dfn[y])。
表格里的数值标注了每个节点的“时间戳” \(dfn\) 和“追溯值” \(low\)。

| 节点 1 | 节点 2 | 节点 3 | 节点 4 | 节点 5 | 节点 6 | 节点 7 | |
|---|---|---|---|---|---|---|---|
| dfn | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| low | 1 | 1 | 1 | 4 | 4 | 4 | 4 |
tarjan 算法与无向图连通性
割边、割点的判定法则
割边
判定法则
在无向图 \(G=(V,E)\) 中,边 \((x,y)\) 是割边,当且仅当该图的搜索树中存在 \(x\) 以及一个 \(x\) 的子节点 \(y\) 满足:
根据定义,dfn[x] < low[y]说明从 son(y) 出发,在不经过边 \((x,y)\) 的前提下,不管走哪条边,都无法到达 \(x\) 或比 \(x\) 更早访问的节点。若把 \((x,y)\) 删除,则son(y) 就好像形成了一个封闭的环境,与节点 \(x\) 没有边相连,图断开成了两部分,因此 \((x,y)\) 是割边。
反之,若不存在这样的子节点 \(y\) 使得 dfn[x] < low[y],则说明每个 son(y) 都能绕行其他边到达 \(x\) 或比 \(x\) 更早访问的节点,\((x,y)\) 自然就不是割边。
不难发现,割边一定是搜索树中的边,并且一个简单环中的边一定都不是割边。
代码实现
#include <iostream>
#define MAXN 20005
#define MAXM 100005
using namespace std;
int n, m, x, y;
struct edge{int to, nxt;}e[MAXM << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], low[MAXN], tot;
bool isb[MAXM << 1], flag;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
cnt++;e[cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void tarjan(int now, int fat){
tot++;dfn[now] = tot;low[now] = tot;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(dfn[v] == 0){
tarjan(v, i);
low[now] = min(low[now], low[v]);
if(dfn[now] < low[v])isb[i] = true,isb[i ^ 1] = true;
}else if(i != (fat ^ 1))
low[now] = min(low[now], dfn[v]);
}
}
int main(){
n = read();m = read();
for(int i = 1 ; i <= m ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)
if(dfn[i] == 0)tarjan(i, 0);
for(int i = 1 ; i <= cnt ; i += 2){
if(isb[i] == true){
write(e[i].to);putchar(' ');
write(e[i ^ 1].to);putchar('\n');
}
}
return 0;
}
运行程序可以得到如下结果:
tsqtsqtsq@MateBook:/mnt/c/Users/tsqtsqtsq/OIer/work$ g++ -o a tarjan.cpp -O2 -st=c++14 -static
tsqtsqtsq@MateBook:/mnt/c/Users/tsqtsqtsq/OIer/work$ time ./a
12 15
1 2
2 3
3 1
3 4
4 5
5 6
6 4
5 7
7 8
8 9
9 7
7 10
9 10
10 11
11 12
3 4
5 7
10 11
11 12
real 0m 0.40s
user 0m 0.00s
sys 0m 0.01s
tsqtsqtsq@MateBook:/mnt/c/Users/tsqtsqtsq/OIer/work$
我们将输入数据绘制成一张图,则有:
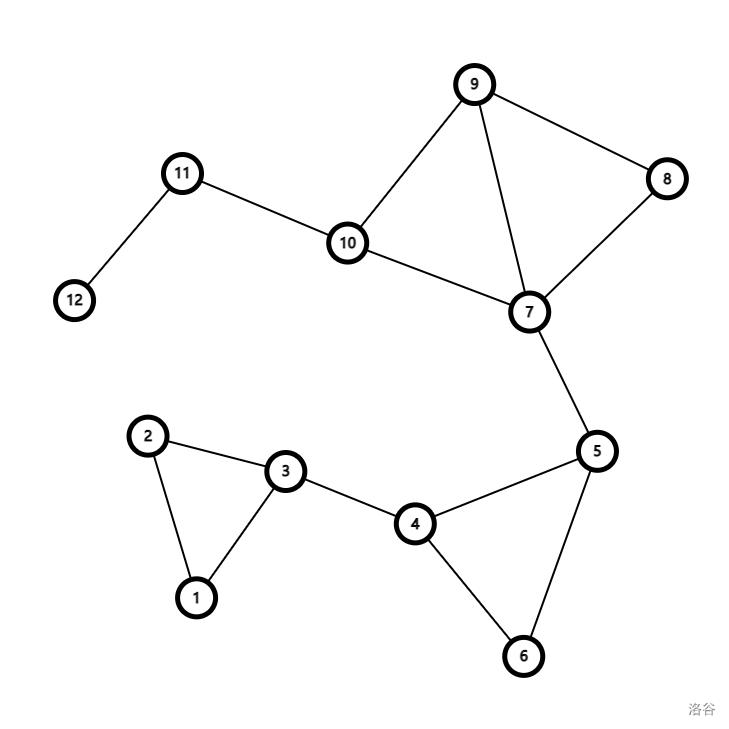
不难发现割边为 \((3,4)\),\((5,7)\),\((10,11)\),\((11,12)\),证明所求是正确的。
割点
判定法则
割点的判定法则类似,只需浅浅修改成这样:
那么,如何一次性地求出图中的所有割点呢?
我们考虑直接运用 tarjan 算法对图进行一次深度优先遍历,遍历时实时更新每一个节点的“时间戳”和“追溯值”。对于每一条边都判一下即可。
有一个特判,如果某个节点是这个搜索树中的根节点,那么一般的割边判定法则对此并不适用。特别地,若 \(x\) 是搜索树的根节点,则 \(x\) 是割点当且仅当搜索树上存在至少两个子节点 \(y_1,y_2\) 满足上述条件。
代码实现
#include <iostream>
#define MAXN 20005
#define MAXM 100005
using namespace std;
int n, m, x, y;
struct edge{int to, nxt;}e[MAXM << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], low[MAXN], tot;
bool ans[MAXN], flag;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
cnt++;e[cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void tarjan(int now, int fat){
tot++;dfn[now] = tot;low[now] = tot;int tmp = 0;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(dfn[v] == 0){
tarjan(v, fat);
low[now] = min(low[now], low[v]);
if(low[v] >= dfn[now] && now != fat)ans[now] = true;
else if(now == fat)tmp++;
}
low[now] = min(low[now], dfn[v]);
}
if(tmp >= 2 && now == fat)ans[now] = true;
}
int main(){
n = read();m = read();
for(int i = 1 ; i <= m ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)
if(dfn[i] == 0)tarjan(i, i);
tot = 0;
for(int i = 1 ; i <= n ; i ++)
if(ans[i] == true)tot++;
write(tot);putchar('\n');
for(int i = 1 ; i <= n ; i ++){
if(ans[i] == true){
if(flag == true)putchar(' ');
write(i);flag = true;
}
}
putchar('\n');return 0;
}
双连通分量的求法
关于双连通分量
若一张无向连通图不存在割点,则称它为“点双连通图”。若一张无向连通图不存在桥,则称它为“边双连通图”。
无向连通图的极大边双连通子图被称为“边双连通分量”,简记为“e-DCC”。无向图的极大点双连通子图被称为“点双连通分量”,简记为“v-DCC”。二者统称为“双连通分量”,简记为"DCC"。
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 边双连通。
在一张连通的无向图中,对于两个点 \(u\) 和 \(v\),如果无论删去哪个点(只能删去一个,且不能删 \(u\) 和 \(v\) 自己)都不能使它们不连通,我们就说 \(u\) 和 \(v\) 点双连通。
边双连通具有传递性,即,若 \(x,y\) 边双连通,\(y,z\) 边双连通,则 \(x,z\) 边双连通。
点双连通 不 具有传递性,反例如下图,\(A,B\) 点双连通,\(B,C\) 点双连通,而 \(A,C\) 不 点双连通。
放点图方便理解(笔者语文水平太 low 不会表达 qwq)
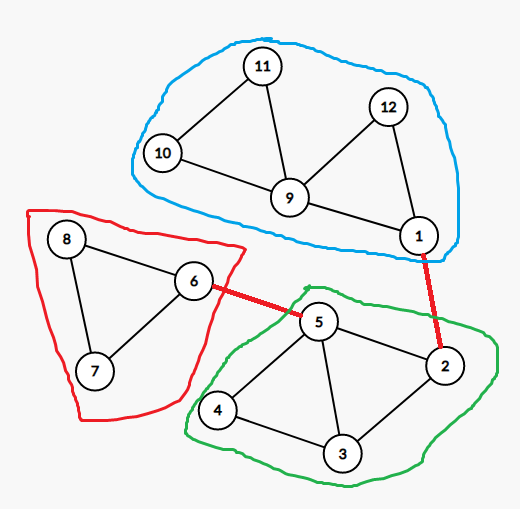
上图中,红边是割边,圈出来的是边双连通分量。
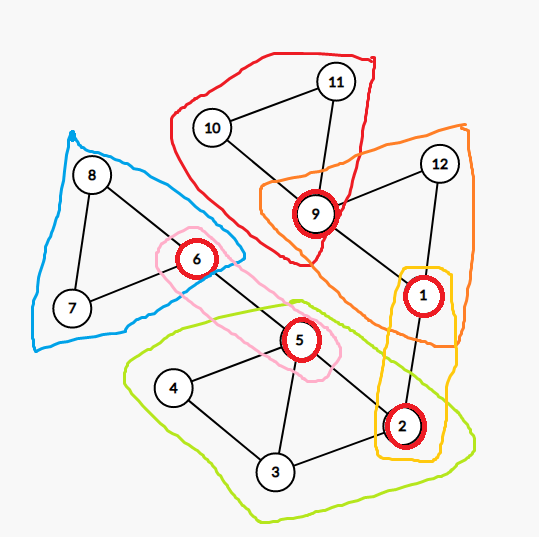
上图中,红点是割点,圈出来的是点双连通分量。
边双连通分量
求法
不难发现,任意两个直接相连的边双连通分量都是由一条割边连接起来的,且一个点只会属于一个边双连通分量。
我们可以先进行一次深度优先遍历找出给定图中的所有割边。求出割边后,再划分出所有边双连通分量:
代码实现
#include <iostream>
#include <vector>
#define MAXN 500005
#define MAXM 2000005
using namespace std;
int n, m, x, y;
struct edge{int to, nxt;}e[MAXM << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], low[MAXN], vis[MAXN], tot;
bool isb[MAXM << 1];
vector <int> ans[MAXN];
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
cnt++;e[cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void tarjan(int now, int fat){
tot++;dfn[now] = tot;low[now] = tot;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(dfn[v] == 0){
tarjan(v, i);
low[now] = min(low[now], low[v]);
if(dfn[now] < low[v])isb[i] = true,isb[i ^ 1] = true;
}else if(i != (fat ^ 1))
low[now] = min(low[now], dfn[v]);
}
}
void dfs(int now, int tim){
vis[now] = tim;ans[tim].push_back(now);
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if (vis[v] == 0 && isb[i] == false)
dfs(v, tim);
}
}
int main(){
n = read();m = read();
for(int i = 1 ; i <= m ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)
if(dfn[i] == 0)tarjan(i, 0);
tot = 0;
for(int i = 1 ; i <= n ; i ++)
if(vis[i] == 0)tot++,dfs(i, tot);
write(tot);putchar('\n');
for(int i = 1 ; i <= tot ; i ++){
write(ans[i].size());
for(int j = 0 ; j < ans[i].size() ; j ++)
putchar(' '),write(ans[i][j]);
putchar('\n');
}
return 0;
}
点双连通分量
求法
知道了割点怎么求,点双连通分量(接下来简称点双)就很好求了:
两个点双最多只有一个公共点(即都有边与之相连的点);且这个点在这两个点双和它形成的子图中是割点。
对于第一点,因为当它们有两个及以上公共点时,它们可以合并为一个新的点双(矩形代表一个点双,圆形代表公共点):
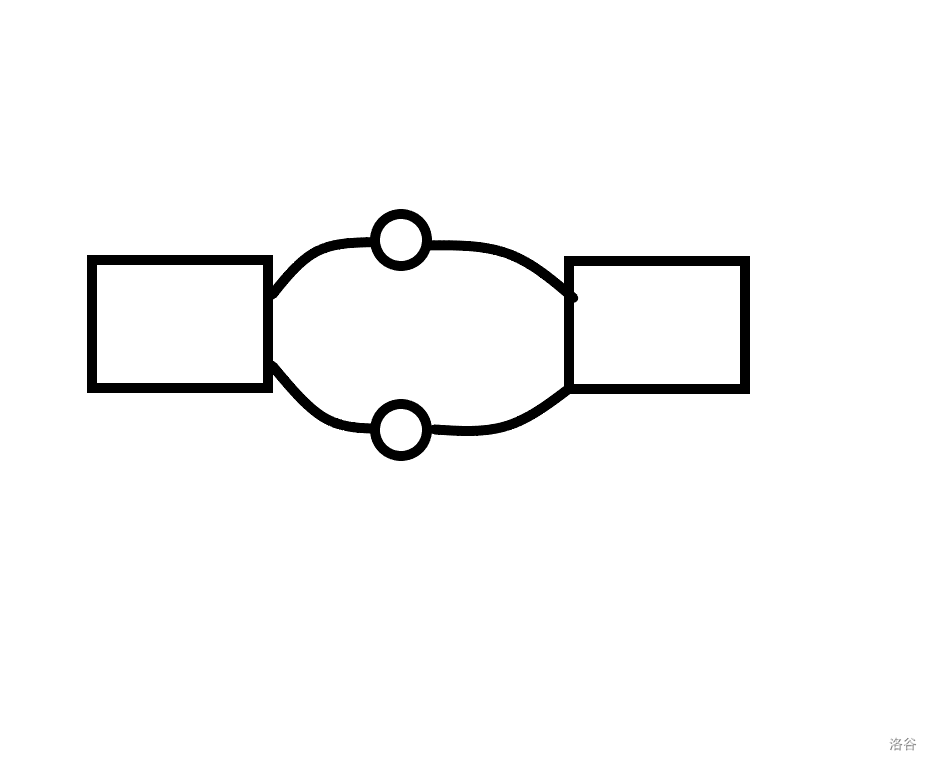
当有两个及以上公共点时,删除其中一个点及其与两个点双相连的边后,这两个点双总是可以通过另一个公共点到达彼此,属于一个连通分量,所以这些公共点对于这个子图而言并不是一个割点,按照定义,这两个点双和这些公共点应该是一个更大的点双。
对于第二点,与第一点类似,当对于这个子图而言它不是一个割点时,这两个点双也可以合并为一个新的点双:
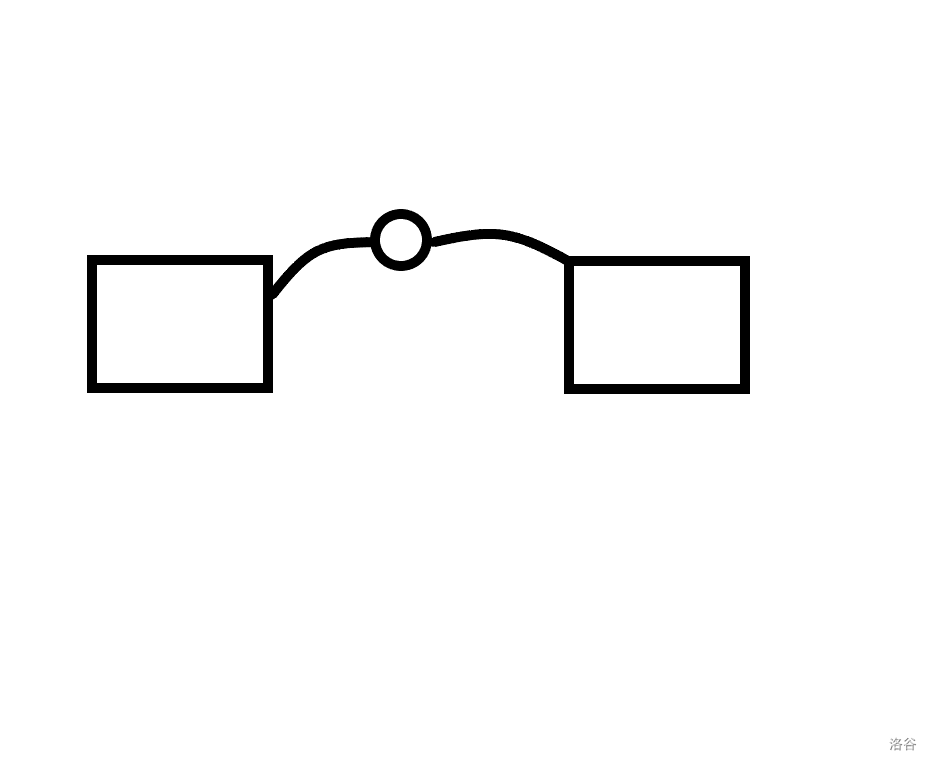
当这个公共点对于这个子图不是一个割点时,也就意味着这两个点双有着另外的边相连,而这些边相连的点同样也是两个点双的公共点,可以归到第一种情况里。
对于一个点双,它在 DFS 搜索树中 dfn 值最小的点一定是割点或者树根。
当这个点是割点时,它所属的点双必定不可以向它的父亲方向包括更多点,因为一旦回溯,它就成为了新的子图的一个割点,不是点双。所以它应该归到其中一个或多个子树里的点双中。
当这个点是树根时,它的 dfn 值是整棵树里最小的。它若有两个以上子树,那么它是一个割点;它若只有一个子树,它一定属于它的直系儿子的点双,因为包括它;它若是一个独立点,视作一个单独的点双。
换句话说,一个点双一定在这两类点的子树中。
我们用栈维护点,当遇到这两类点时,将子树内目前不属于其它点双的非割点或在子树中的割点归到一个新的点双。注意这个点可能还是与其它点双的公共点,所以不能将其出栈。
代码实现
#include <iostream>
#include <vector>
#define MAXN 500005
#define MAXM 2000005
using namespace std;
int n, m, x, y;
struct edge{int to, nxt;}e[MAXM << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], low[MAXN], tot;
int stk[MAXN], top, sum;
vector <int> ans[MAXN];
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
cnt++;e[cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void tarjan(int now, int fat){
tot++;dfn[now] = tot;low[now] = tot;
top++;stk[top] = now;int son = 0;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(dfn[v] == 0){
son++;tarjan(v, now);
low[now] = min(low[now], low[v]);
if(low[v] >= dfn[now]){
sum++;
while(stk[top + 1] != v)
ans[sum].push_back(stk[top]),top--;
ans[sum].push_back(now);
}
}else if(v != fat)
low[now] = min(low[now], dfn[v]);
}
if(fat == 0 && son == 0)sum++,ans[sum].push_back(now);
}
int main(){
n = read();m = read();
for(int i = 1 ; i <= m ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)
if(dfn[i] == 0)top = 0,tarjan(i, 0);
write(sum);putchar('\n');
for(int i = 1 ; i <= sum ; i ++){
write(ans[i].size());
for(int j = 0 ; j < ans[i].size() ; j ++)
putchar(' '),write(ans[i][j]);
putchar('\n');
}
return 0;
}
tarjan 算法与有向图连通性
关于强连通分量
若一张有向图的节点两两互相可达,则称这张图是 强连通的 (strongly connected)。
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
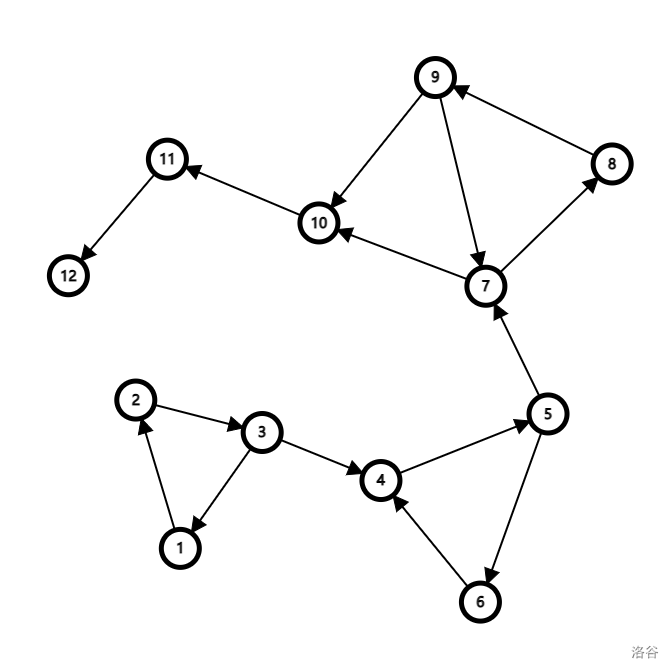
上图中,一共有 5 个强连通分量 \(\left\{1,2,3\right\}\),\(\left\{4,5,6\right\}\),\(\left\{7,8,9\right\}\),\(\left\{10\right\}\),\(\left\{11\right\}\),\(\left\{12\right\}\)。
求法
在 Tarjan 算法中为每个结点 \(u\) 维护了以下几个变量:
- \(\textit{dfn}_u\):深度优先搜索遍历时结点 \(u\) 被搜索的次序。
- \(\textit{low}_u\):在 \(u\) 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(\textit{Subtree}_u\)。\(\textit{low}_u\) 定义为以下结点的 \(\textit{dfn}\) 的最小值:\(\textit{Subtree}_u\) 中的结点;从 \(\textit{Subtree}_u\) 通过一条不在搜索树上的边能到达的结点。
一个结点的子树内结点的 dfn 都大于该结点的 dfn。
从根开始的一条路径上的 dfn 严格递增,low 严格非降。
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索,维护每个结点的 dfn 与 low 变量,且让搜索到的结点入栈。每当找到一个强连通元素,就按照该元素包含结点数目让栈中元素出栈。在搜索过程中,对于结点 \(u\) 和与其相邻的结点 \(v\)(\(v\) 不是 \(u\) 的父节点)考虑 3 种情况:
- \(v\) 未被访问:继续对 \(v\) 进行深度搜索。在回溯过程中,用 \(\textit{low}_v\) 更新 \(\textit{low}_u\)。因为存在从 \(u\) 到 \(v\) 的直接路径,所以 \(v\) 能够回溯到的已经在栈中的结点,\(u\) 也一定能够回溯到。
- \(v\) 被访问过,已经在栈中:根据 low 值的定义,用 \(\textit{dfn}_v\) 更新 \(\textit{low}_u\)。
- \(v\) 被访问过,已不在栈中:说明 \(v\) 已搜索完毕,其所在连通分量已被处理,所以不用对其做操作。
对于一个连通分量图,我们很容易想到,在该连通图中有且仅有一个 \(u\) 使得 \(\textit{dfn}_u=\textit{low}_u\)。该结点一定是在深度遍历的过程中,该连通分量中第一个被访问过的结点,因为它的 dfn 和 low 值最小,不会被该连通分量中的其他结点所影响。
因此,在回溯的过程中,判定 \(\textit{dfn}_u=\textit{low}_u\) 是否成立,如果成立,则栈中 \(u\) 及其上方的结点构成一个 SCC。
代码实现
#include <iostream>
#include <vector>
#define MAXN 20005
#define MAXM 100005
using namespace std;
int n, m, x, y;
struct edge{int to, nxt;}e[MAXM << 1];
int head[MAXN], cnt = 1;
int dfn[MAXN], low[MAXN], vis[MAXN], tot, sum;
int stk[MAXN], top;
bool ins[MAXN];
vector <int> ans[MAXN];
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
}
void tarjan(int now){
tot++;dfn[now] = tot;low[now] = tot;
top++;stk[top] = now;ins[now] = true;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(dfn[v] == 0){
tarjan(v);low[now] = min(low[now], low[v]);
}else if(ins[v] == true)
low[now] = min(low[now], dfn[v]);
}
if(dfn[now] == low[now]){
sum++;
while(stk[top + 1] != now){
vis[stk[top]] = sum;
ins[stk[top]] = false;top--;
}
}
}
int main(){
n = read();m = read();
for(int i = 1 ; i <= m ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)
if(dfn[i] == 0)tarjan(i);
for(int i = 1 ; i <= n ; i ++)
ans[vis[i]].push_back(i);
for(int i = 1 ; i <= sum ; i ++){
write(ans[i].size());
for(int j = 0 ; j < ans[i].size() ; j ++)
putchar(' '),write(ans[i][j]);
putchar('\n');
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号