SZTU-ACM 2021 春期训练赛第一场 [组队赛]总结和题解
比赛总结
这场比赛是组队后进行的第一场组队训练赛,最后做了八道题。作为第一次比赛的成绩,也已经还算不错了,不过还是要对比赛中出现的一些问题进行总结反思。这场比赛,前期由于我的失误,在签到题wa了一发,导致前期节奏不够好,之后大家分开开题,我写了c,队友写了b。另一个队友在推后面题的式子。之后,我把一个字典序的简单题水了过去,时间已经过去了两个小时,我们三个分开看三个题,我去写了一个数学题,一个队友去写大模拟,另一个队友用矩阵快速幂把开局看的题写了一下,这段时间应该算一个小的爆发期,在三小时的时候我们把这三个题都通过了,此时还剩两个小时,剩三道题。但是,由于后期时间分配不合理,导致本来可做的D题没有时间写了。队友刚开始写高斯消元的板子,但是可能是精度问题,一直没有过题,我因为对压轴题题意的错误理解,导致在压轴题上浪费了大量时间。直到最后队友才把E题调对,这时候时间已经不支持我们继续开题了。所以这场比赛最后以八题收尾了。虽然成绩还算不错,不过还是要认识到自己知识点的不全面。和对题目难度判断的不准确争取下次取得更好的成绩
A - hzy 和zsl 的生存挑战
这道题目关键在于他们可以提前制定策略,一个人猜另一个人和自己一样,一个人猜另一个人和自己不一样,一定能保证有一种答案是正确的。所以四行都输出1.00即可。
#include<bits/stdc++.h>
using namespace std;
int main()
{
cout<<"1.00"<<endl;
cout<<"1.00"<<endl;
cout<<"1.00"<<endl;
cout<<"1.00"<<endl;
return 0;
}
B - 人类史上最大最好的希望事件
这道题题目有点难读,但是理解后很容易发现,就是一个对斐波那契数列平方维护的前缀和问题,数据范围较小,我们不用矩阵快速幂,直接斐波那契数列和前缀和就能解决问题。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX=1e6+5;
const int mod=192600817;
ll f[201010],f2[201010],sf2[201010];
int main()
{
f[0]=f[1]=1;
for(int i=2;i<101000;i++)f[i]=(f[i-2]+f[i-1])%mod;
for(int i=0;i<101000;i++)
{
f2[i]=f[i]*f[i]%mod;
if(i==0)sf2[i]=1;
else sf2[i]=(sf2[i-1]+f2[i])%mod;
}
int Q,a,b,c,d;
while(cin>>Q)
{
while(Q--)
{
scanf("%d%d%d%d",&a,&b,&c,&d);
ll L=a*4+b;
ll R=c*4+d;
if(L>R)swap(L,R);
ll ans= L==0?sf2[R]:(sf2[R]-sf2[L-1]+mod)%mod;
printf("%lld\n",ans);
}
}
}
C - 超级无敌简单题
观察可以发现如果超过16次还没有变成0,会形成循环节,所以只需要限制每个数的迭代次数就能解决这个问题。暴力求出即可
#include<bits/stdc++.h>
using namespace std;
long long a[150010];
void work()
{
long long q = 1,ww,now,ans;
for (long long i = 1;i<=1045000;i++){
ww = 0,now = i;
while (ww<=15){
ww++;
ans = 0;
while (now)
ans += (now%10)*(now%10),now/=10;
now = ans;
if (now == 1) break;
if (now == 4) ww = 16;
}
if (ww<=15)
a[q++] = i;
}
}
int main()
{
work();
int q;
scanf("%d",&q);
while (q--){
int x;
scanf("%d",&x);
printf("%d\n",a[x]);
}
return 0;
}
D - 免费送气球
可以先离线处理所有数据,把数据离散化,然后用两个树状数组分别维护每个值的个数和区间和。在求解情况二的时候,我们把问题分成三个部分第一部分就是 :第一个下标所在的地方 (求个数×对应的值)第二部分就是:第二个下标的所在的地方(求个数×对应的值)第三部分就是:两个下标中间连续的一大块(直接用区间和)。然后就可以求出答案了,树状数组可以用线段树代替。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+100;
const int mod = 1e9+7;
typedef struct Node {
ll x,y;
}a [N] ;
ll b[N],tot,c1[N],c2[N]; //c1维护区间个数,c2维护区间和
int op[N];
void add1(int No,ll val){
while(No<N){
c1[No] += val;
No += (No&-No);
}
}
void add2(int No,ll val){ //更新 个数对应的区间总和
while(No<N){
c2[No] += val;
No += (No&-No);
}
}
ll sum1(int No){ //求和 个数求和
ll res = 0;
while( No>0 ){
res += (c1[No]);
No -= No&-No;
}
return res;
}
ll sum2(int No){ //求和 区间的求和
ll res = 0;
while( No>0 ){
res = (c2[No]+res)%mod;
No -= (No & -No);
}
return res;
}
int getblock(ll x){ //知道某一次询问的下标在哪一块
ll L = 1 ,R = tot,ans=1,Mid;
while( L<=R ){
Mid = (L+R) >> 1;
if( sum1(Mid) < x ){
L = Mid +1;
ans = Mid;
}else{
R = Mid -1;
}
}
return L ;
}
int main()
{
int n,m;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%lld%lld",&op[i],&a[i].x,&a[i].y);
if( op[i] == 1 )
b[++tot] = a[i].y;//离线离散化
}
sort( b+1, b+1+tot);
for(int i=1;i<=n;i++){
if( op[i] == 1 ){
int pos = lower_bound(b+1,b+1+tot,a[i].y)-(b);//找到合适的位置插入,维护序列有序
add1( pos ,a[i].x);//建立每个值个数的树状数组
add2( pos ,(a[i].x*a[i].y)%mod);// 建立每个值的总和的
}else{
int L = getblock(a[i].x); //获取下标x所在的块
int R = getblock(a[i].y); //获取下标y所在的块
ll t1,t2,t3;
t1 = t2 = t3 = 0;
t1 = ( (sum1(L) - a[i].x+1+mod)%mod * b[L] )%mod; // L所在的块中的个数×b[L]
t2 = ( (a[i].y - sum1(R-1)+mod)%mod * b[R] )%mod; // R所在的块中的个数×b[R]
t3 = (sum2(R-1) - sum2(L) + mod )%mod; // 中间部分
ll ans = (t1 + t2 + t3) %mod;
printf("%lld\n",ans);
}
}
return 0;
}
E - 水题
我们先求出刚开始的后面两个点对于第一个点的向量,在求出变换之后后面两个点对于第一个点的向量,这是个线性变换,那么12的矩阵要得到12的矩阵,只有乘上2*2的矩阵,求出这个矩阵之后,对于每个给你的点,先求出它关于三角形第一个点变换之前的向量,乘上这个矩阵得到变换之后的向量,再加上三角形第一个点变换之后的坐标即可。
#include<bits/stdc++.h>
using namespace std;
int main()
{
double x[10],y[10];
int t;
scanf("%d",&t);
while(t--)
{
for(int i=1;i<=6;i++)
scanf("%lf%lf",&x[i],&y[i]);
double a,b,c,d;
for(int i=2;i<=3;i++)
x[i]-=x[1],y[i]-=y[1];
for(int i=5;i<=6;i++)
x[i]-=x[4],y[i]-=y[4];
c=(x[5]*x[3]-x[6]*x[2])/(y[2]*x[3]-x[2]*y[3]);
a=(x[5]-y[2]*c)/x[2];
d=(y[5]*x[3]-y[6]*x[2])/(y[2]*x[3]-x[2]*y[3]);
b=(y[5]-y[2]*d)/x[2];
int q;
scanf("%d",&q);
while(q--)
{
scanf("%lf%lf",&x[2],&y[2]);
x[2]-=x[1],y[2]-=y[1];
printf("%.2f %.2f\n",x[2]*a+y[2]*c+x[4],x[2]*b+y[2]*d+y[4]);
}
}
return 0;
}
这里再放一个队友的代码
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
int T, Q;
double sX[3], sY[3], dX[3], dY[3];
double sMat[3][4];
double aMat[3];
void Gauss() {
memset(aMat, 0x0, sizeof(aMat));
for (int row = 0, col = 0; row < 3 && col < 4; ++row, ++col) {
int mxr = row;
for (int i = row + 1; i < 3; ++i)
if (fabs(sMat[i][col]) > fabs(sMat[mxr][col]))
mxr = i;
if (mxr != row)
for (int i = row; i < 4; ++i)
std::swap(sMat[row][i], sMat[mxr][i]);
if (fabs(sMat[row][col]) < 1e-6) {
--row;
continue;
}
for (int i = row + 1; i < 3; ++i)
if (fabs(sMat[i][col]) > 1e-6) {
double tmp = sMat[i][col] / sMat[row][col];
for (int j = col; j < 4; ++j)
sMat[i][j] -= sMat[row][j] * tmp;
sMat[i][col] = 0.0;
}
}
for (int i = 2; i >= 0; --i) {
double tmp = sMat[i][3];
for (int j = i + 1; j < 3; ++j)
tmp -= sMat[i][j] * aMat[j];
aMat[i] = tmp / sMat[i][i];
}
}
double a, b, c, d, e, f;
int main() {
scanf("%d", &T);
while (T--) {
for (int i = 0; i < 3; ++i)
scanf("%lf%lf", &sX[i], &sY[i]);
for (int i = 0; i < 3; ++i)
scanf("%lf%lf", &dX[i], &dY[i]);
a = (dX[0] - dX[2] - (dX[0] - dX[1]) * (sY[0] - sY[2]) / (sY[0] - sY[1])) / (sX[0] - sX[2] - (sX[0] - sX[1]) * (sY[0] - sY[2]) / (sY[0] - sY[1]));
b = (dX[0] - dX[1] - a * (sX[0] - sX[1])) / (sY[0] - sY[1]);
e = dX[0] - a * sX[0] - b * sY[0];
c = (dY[0] - dY[2] - (dY[0] - dY[1]) * (sY[0] - sY[2]) / (sY[0] - sY[1])) / (sX[0] - sX[2] - (sX[0] - sX[1]) * (sY[0] - sY[2]) / (sY[0] - sY[1]));
d = (dY[0] - dY[1] - c * (sX[0] - sX[1])) / (sY[0] - sY[1]);
f = dY[0] - c * sX[0] - d * sY[0];
scanf("%d", &Q);
double x, y;
while (Q--) {
scanf("%lf%lf", &x, &y);
printf("%.2f %.2f\n", x * a + y * b + e, x * c + y * d + f);
}
}
return 0;
}
F - 清一色
这是个纯模拟题,没什么太多可以说的,按照题意慢慢写就行了
#include<bits.stdc++.H>
int shunzi, kezi, fj = 0;
int pai[15], cnt[15];
inline int read_int()
{
char c;
int sign = 1;
while((c = getchar()) < '0' || c > '9')
if(c == '-') sign = -1;
int res = c - '0';
while((c = getchar()) >= '0' && c <= '9')
res = res * 10 + c - '0';
return res * sign;
}
void to_sz(int x);
void to_kz(int x);
bool is_dz()
{
int ans = 0;
for(int i = 1; i <= 9; i++)
{
if(pai[i] == 2) ans++;
}
if(ans == 7) return true;
return false;
}
bool is_qys()
{
kezi = 0, shunzi = 0, fj = 0;
for(int i = 1; i <= 9; i++)
{
pai[i] = cnt[i];
}
if(is_dz()) return true;
to_sz(0);
to_kz(0);
if(fj) return true;
else return false;
}
void judg()
{
for(int i = 1; i <= 9; i++)
{
if(pai[i] == 2) fj = 1;
}
}
void to_sz(int x)
{
if(x == 4)
{
judg();
}
for(int i = 1; i <= 9; i++)
{
if(pai[i] >= 3)
{
pai[i] -= 3;
to_sz(x + 1);
to_kz(x + 1);
pai[i] += 3;
}
}
}
void to_kz(int x)
{
if(x == 4)
judg();
for(int i = 1; i <= 7; i++)
{
if(pai[i] && pai[i + 1] && pai[i + 2])
{
pai[i]--, pai[i + 1]--, pai[i + 2]--;
to_sz(x + 1);
to_kz(x + 1);
pai[i]++, pai[i + 1]++, pai[i + 2]++;
}
}
}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
if(!n) break;
for(int i = 1; i <= 9; i++)
{
cnt[i] = 0;
}
cnt[n]++;
for(int i = 1; i <= 13; i++)
{
int x = read_int();
cnt[x]++;
}
//自摸
if(is_qys())
{
printf("tsumo\n");
continue;
}
//听牌
int f = 0;
for(int i = 1; i <= 9; i++)
{
int x_y = 0;
for(int j = 1; j <= 9; j++)
{
if(cnt[i] && cnt[j] < 4 && i != j)
{
cnt[i]--, cnt[j]++;
if(is_qys())
{
f++;
if(f == 1) printf("tenpai");
if(!x_y)
{
x_y++;
printf("\n%d:", i);//x
}
printf(" %d", j);//y
}
cnt[i]++, cnt[j]--;
}
}
}
if(!f) printf("noten");
printf("\n");
}
return 0;
}
G - 简单数学题
[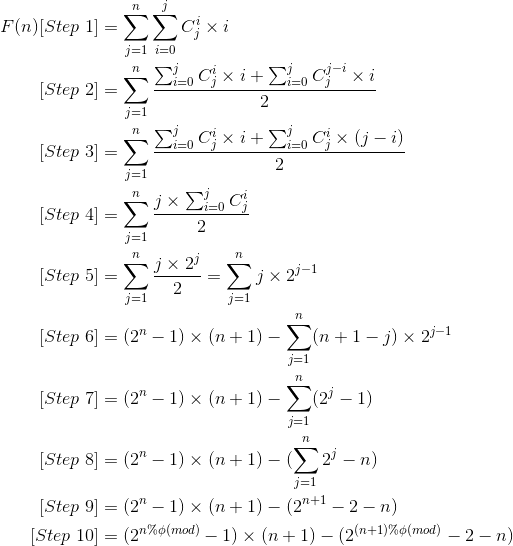 ]
]
这是题目严格按照组合数学推导的到的最简式,我们也可以打表观察发现公式为(i−1)∗2的i次方 +1。
然后用快速幂优化就可以求出答案
#include<bits/stdc++.h>
using namespace std;
long long mod = 1e9+7;
long long int pow1(long long int q){
long long ans = 1,a = 2;
while(q){
if(q&1)
ans=(ans*a)%mod;
a = a*a%mod;
q>>=1;
}
return ans;
}
int main()
{
long long int n;
while(~scanf("%lld",&n))
{
long long int ans1=((n-1)%mod*pow1(n)%mod+1)%mod;
printf("%lld\n",ans1);
}
return 0;
}
H - zyb的面试
这个题我们就按照题目要求,枚举每一个字典序就能解决问题,关键是根据给出的数字范围,我们确定字典树的枚举顺序,本质就是dfs去处理一颗十叉树的过程,按照dfs顺序判断当前数字字典序大小。
#include<bits/stdc++.h>
using namespace std;
int t,n,k;
void solve(int k)
{
int x=1,q=1;
while(q<k)
{
if(x*10<=n)
x=x*10,q++;
else{
if(x+1<=n)
{
while(x%10==9)
x=x/10;
x++,q++;
}
else{
x=x/10;
while(x%10==9)
x=x/10;
x++,q++;
}
}
}
printf("%d\n",x);
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
solve(k);
}
return 0;
}
I - 故事
我们可以先把题目转化为给你一棵树,问你从顶端走到底端,你最多能走q个点,问你能走到最多多少叶子结点。于是我们可以二分能走到的叶子结点有多少个,然后从下往上除上一个节点的儿子个数,这样就可以知道上一个节点有多少个,如果每个节点的儿子数都大于2的话,需要注意的是,如果当前节点只有1个儿子结点我们直接把他练到下一个叶子节点上,并将权值修改为2.
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
long long son[N],val[N];
int n,q,all;
int check(ll mid,ll x)
{
int sum=n;
for(int i=1;i<=all;i++)
{
if(mid==1)
return (x-sum)>=0;
sum-=val[i];
x-=mid*val[i];
if(i<all)
mid=(mid+son[i+1]-1)/son[i+1];
if(x<0)
return 0;
}
return 1;
}
int main()
{
scanf("%d%d",&n,&q);
scanf("%d",&son[1]);
all=1,val[1]=1;
long long x,pointmax=1;
for(int i=2;i<=n;i++)//建树
{
scanf("%lld",&x);
if(pointmnax<=1e9)
pointmax*=x;
if(x==1)
val[all]++;
else
son[++all]=x,val[all]=1;
}
while(q--)
{
scanf("%d",&x);
long long low=0,high=min((long long)1e9,pointmax),mid,ans=0;
while(high>=low)
{
mid=low+high>>1;
if(check(mid,x))
low=mid+1,ans=mid;
else
high=mid-1;
}
printf("%lld\n",ans*son[1]);
}
return 0;
}
J - Count
递推式为f(n)=f(n-1)+2*f(n-1)+n^3
构建矩阵
1 2 1 0 0 0
1 0 0 0 0 0
0 0 1 3 3 1
0 0 0 1 2 1
0 0 0 0 1 1
0 0 0 0 0 1
直接矩阵快速幂就能得到结果了
#include <cstdio>
#include <cstring>
#define il inline
#define ll long long
#define MOD 123456789
ll T, n;
il int trs(int x, int y) {
return x * 6 + y;
}
void m6xm6(ll a[6][6], ll b[6][6], ll* c) {
memset(c, 0x0, 36 * sizeof(ll));
for (int i = 0; i < 6; ++i)
for (int j = 0; j < 6; ++j)
for (int k = 0; k < 6; ++k) {
c[trs(i, j)] += a[i][k] * b[k][j];
c[trs(i, j)] %= MOD;
}
}
ll m6xv6(ll a[6][6], ll b[6]) {
ll c = 0;
for (int i = 0; i <6; ++i) {
c += a[0][i] * b[i];
c %= MOD;
}
return c;
}
ll qpow(ll n) {
ll ans[6][6], b[6][6], tmp[36];
memset(ans, 0x0, sizeof(ans));
for (int i = 0; i < 6; ++i)
ans[i][i] = 1;
memset(b, 0x0, sizeof(b));
b[0][0] = b[0][2] = b[1][0] = b[2][2] = b[2][5] = b[3][3] = b[3][5] = b[4][4] = b[4][5] = b[5][5] = 1;
b[0][1] = b[3][4] = 2;
b[2][3] = b[2][4] = 3;
while (n) {
if (n & 1) {
m6xm6(ans, b, tmp);
memcpy(ans, tmp, sizeof(ans));
}
m6xm6(b, b, tmp);
memcpy(b, tmp, sizeof(b));
n >>= 1;
}
ll v6[6] = {2, 1, 27, 9, 3, 1};
return m6xv6(ans, v6);
}
int main() {
scanf("%lld", &T);
while (T--) {
scanf("%lld", &n);
printf("%lld\n", qpow(n - 2));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号