uva 10129 单词

题目：
输入n个单词，是否可以把这些单词排成一个序列，使得第一个字母和上一个单词的最后一个字母相同。仅包含小写字母例如（acm malform mouse）就可以。

看到这个问题我们需要先介绍一下著名的欧拉回路，欧拉回路：最先由著名的七桥问题提出，如果一个无向图是连通的，且最多只有两个奇点，则一定存在欧拉回路。最多只能有两个点的入度不等于出度，而且最终必须是其中一个点的出度恰好比入度大1（把它作为起点），另一个入度比出度大1（把它作为终点）。同时还要满足图的联通性，我们可以从七桥问题简单分析这个问题

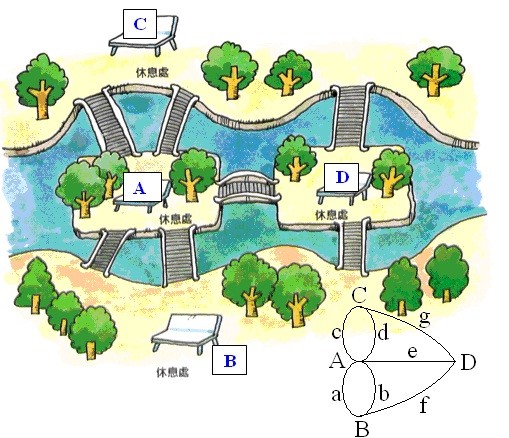
我们可以发现，在这个问题中所有的边的度数都是奇数，一定无法满足形成欧拉回路的条件。

继续看回本题的要求，一共有26个字母作为节点，统计每个单词的首尾字母看为一条边。由于这是有向图，分开统计入读和出度。然后在dfs判断是否

联通，就可以判断是否存在欧拉回路了

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
char s[maxn];
int g[maxn][maxn],in[maxn],out[maxn],vis[maxn];//in代表入度out代表出度，vis代表是否访问过。邻接矩阵存图 
void dfs(int u){
    vis[u] = 1;
    for(int i = 0;i < 26;i++){
        if(!vis[i] && g[u][i])//如果未被访问过，且有有向边，继续dfs
            dfs(i);
    }
}
int main()
{
    int t,n;
    cin>>t;
    while(t--){
        memset(g,0,sizeof(g));memset(in,0,sizeof(in));
        memset(out,0,sizeof(out));memset(vis,0,sizeof(vis));
        cin>>n;
        for(int i = 0;i < n;i++){
            cin>>s;
            int f = s[0]-'a';//通过ASC码将字符转换为方便遍历的整数类型
            int l = s[strlen(s)-1] - 'a';
            in[l]++;
            out[f]++;
            g[f][l]++;//记录每个字母的入度出度和存边。 
        }
        bool flag = true,connect = true;
        int head = 0,last = 0;
        for(int i = 0;i < 26;i++){
            if(in[i] == out[i]) continue;
            if(out[i] == in[i]+1) head++;
            else if(in[i] == out[i]+1) last++;
            else {flag = false;break;}//这里代表除了头和尾外出现了奇度顶点。
        }
        if(head && last && head+last>2) flag = false;//连通度大于1
        if(flag){
            for(int i = 0;i < 26;i++){
                if(out[i] == in[i]+1 || (head == 0&&last==0)){
                    dfs(i);//从起点开始dfs
                    break;
                }
            }
            for(int i = 0;i < 26;i++){
                if(!vis[i] && in[i]){
                    connect = false;break;
                }
                if(!vis[i] && out[i]){
                    connect = false;break;
                }
            }
            } 
            if(connect&&flag) cout<<"Ordering is possible."<<endl;
            else cout<<"The door cannot be opened."<<endl;
    }
    return 0;
}