USACO 2018 Open 题解
USACO 2018 Open Solution
- USACO 2018 Open Solution
- 更好的阅读体验戳此进入
- 题面 Luogu 链接
- LG-P4379 [USACO18OPEN]Lemonade Line S
- LG-P4380 [USACO18OPEN]Multiplayer Moo S
- LG-P4376 [USACO18OPEN]Milking Order G
- LG-P4377 [USACO18OPEN] Talent Show G
- LG-P4378 [USACO18OPEN]Out of Sorts S
- LG-P4375 [USACO18OPEN]Out of Sorts G
- LG-P4372 [USACO18OPEN]Out of Sorts P
- LG-P4374 [USACO18OPEN]Disruption P
- LG-P4373 [USACO18OPEN]Train Tracking P
- UPD
更好的阅读体验戳此进入
题面 Luogu 链接
LG-P4379 [USACO18OPEN]Lemonade Line S
题面
娱乐题,读完题你们肯定也都秒了。。
有 $ n $ 头牛,每头有 $ w_i $ 表示最多可以忍受多少头牛在其前面排队,每头牛都会尝试排到队尾一次,如果不可行便不会再去排,求一个尝试排队的顺序以最小化最终队列中的牛的数量,求最小值。
Examples
Input_1
5 7 1 400 2 2
Output_1
3
Solution
没啥可说的,无脑贪心,排个序即可。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
vector < int > cow;
int ans(0);
int main(){
N = read();
for(int i = 1; i <= N; ++i)cow.emplace_back(read());
sort(cow.begin(), cow.end(), greater < int >());
for(auto it = cow.begin(); it != cow.end(); ++it)if(*it >= ans)++ans; else break;
printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4380 [USACO18OPEN]Multiplayer Moo S
题面
存在一个 $ n \times n $ 网格图,每格一个数,定义连通块为四联通的相同的数构成区域,求最大的连通块的大小,以及有且仅有两种数字的最大的连通块的大小。
$ 1 \le n \le 250 $。
Examples
Input_1
4 2 3 9 3 4 9 9 1 9 9 1 7 2 1 1 9
Output_1
5 10
Solution
第一眼我就感觉这玩意和一个特别远古的经典题《宽搜 海战》特别像,那道题大概就是描述一个 $ 01 $ 矩阵然后让你求四连通块数量,然后发现确实差不多。。第一问的话就是记录一下是否访问过,然后遍历每个点,没访问过的话就搜一下,搜这个点所在的整个连通块,标记一下,然后记录块大小之类的,最后枚举一下取 $ \max $ 即可。。然后后来翻了一下题解才知道这玩意还有个名字叫 FloodFill,我一直以为这玩意就是朴素宽搜呢。。
然后对于第二问,我们可以考虑把每块缩一下,然后相邻的不同块建边,在这里枚举所有块,再枚举其相连的块,然后跑一个类似宽搜的东西,无脑枚举还有哪些块是连通的,每次算完取 $ \max $ 即可,当然这玩意的时空复杂度都很玄学,中间很多判重,可以考虑用 set 或 unorderer_set 加手写哈希实现,然后发现这玩意会 $ \texttt{TLE} $,各种卡常之后依然寄,于是尝试思考为什么被卡,显然如果想要卡满算法应该让每个块大小均为 $ 1 $ 且隔一个块之后又是自己相同的颜色,这样第二问每次都会搜满图,然后枚举也是 $ O(n^2) $ 级别的,最后差不多 $ O(n^4) $,所以会寄。于是我们考虑,如果是这种类型的图一定会在很大部分均为最大值,所以可以不需要枚举完所有点对,加个卡时即可,很难被卡掉,即使被卡了也可以通过 rand 取点并判重,可以让出解率极高。
当然上面都是我口糊的,正解似乎可以通过 map 判重之类的实现,反正也算是暴力枚举加剪枝过的。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define IN_RANGE(x, y) (1 <= x && x <= N && 1 <= y && y <= N)
template< typename T = int >
inline T read(void);
int N;
int mp[300][300];
int belong[300][300];
// bitset < 90000 > exist[90000];
struct HashPair{
size_t operator() (const pair < int, int > &x)const{
// auto hash1 = hash < int >{}(x.first);
// auto hash2 = hash < int >{}(x.second);
// return hash1 ^ hash2;
return (ll)x.first * x.second % (1000000007);
}
};
unordered_set < pair < int, int >, HashPair > exist;
int mx1(-1), mx2(-1);
int cnt(0);
pair < int, int > blk[110000];
bitset < 90000 > vis[1];
int ver(0);
int dx[10] = {0, -1, 0, 1, 0};
int dy[10] = {0, 0, 1, 0, -1};
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[910000];
ROPNEW(ed);
Edge* head[210000];
void bfs(int idx, int val, int px, int py){
queue < pair < int, int > > cur;
cur.push({px, py});
belong[px][py] = idx;
++blk[idx].second;
while(!cur.empty()){
auto tp = cur.front(); cur.pop();
for(int i = 1; i <= 4; ++i){
int tx = tp.first + dx[i], ty = tp.second + dy[i];
if(!IN_RANGE(tx, ty))continue;
if(mp[tx][ty] == val && !belong[tx][ty])++blk[idx].second, belong[tx][ty] = idx, cur.push({tx, ty});
}
}
}
int main(){
N = read();
for(int i = 1; i <= N; ++i)for(int j = 1; j <= N; ++j)mp[i][j] = read();
for(int i = 1; i <= N; ++i)
for(int j = 1; j <= N; ++j)
if(!belong[i][j]){
blk[++cnt].first = mp[i][j];
bfs(cnt, mp[i][j], i, j);
}
for(int i = 1; i <= N; ++i)
for(int j = 1; j <= N; ++j)
for(int k = 1; k <= 4; ++k){
int tx = i + dx[k], ty = j + dy[k];
if(IN_RANGE(tx, ty) && belong[tx][ty] != belong[i][j]){
int t = belong[tx][ty], s = belong[i][j];
if(exist.find(make_pair(s, t)) == exist.end()){
exist.insert({s, t});
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
}
}
}
// for(int i = 1; i <= cnt; ++i)printf("blk[%d] = %d\n", i, blk[i].second);
for(int i = 1; i <= cnt; ++i)mx1 = max(mx1, blk[i].second);
// printf("Belong:\n");
// for(int i = 1; i <= N; ++i)for(int j = 1; j <= N; ++j)printf("%d%c", belong[i][j], j == N ? '\n' : ' ');
// for(int p = 1; p <= cnt; ++p){
// printf("Father: %d: ", p);
// for(auto i = head[p]; i; i = i->nxt){
// printf("%d ", SON);
// }printf("\n");
// }
queue < int > tmp;
queue < int > undel;
for(int p = 1; p <= cnt; ++p)
for(auto t = head[p]; t; t = t->nxt){
if((double)clock() / CLOCKS_PER_SEC > 0.9)printf("%d\n%d\n", mx1, mx2), exit(0);
while(!undel.empty()){
int tp = undel.front(); undel.pop();
vis[ver][tp] = false;
}
int ans(0);
// ++ver;
// vis[ver].reset();
vis[ver][p] = vis[ver][t->to] = true;
undel.push(p), undel.push(t->to);
tmp.push(p), tmp.push(t->to);
ans += blk[p].second, ans += blk[t->to].second;
while(!tmp.empty()){
int tp = tmp.front(); tmp.pop();
for(auto i = head[tp]; i; i = i->nxt){
if(vis[ver][SON])continue;
if(blk[SON].first == blk[p].first || blk[SON].first == blk[t->to].first){
vis[ver][SON] = true;
undel.push(SON);
tmp.push(SON);
ans += blk[SON].second;
}
}
}
mx2 = max(mx2, ans);
}
printf("%d\n%d\n", mx1, mx2);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4376 [USACO18OPEN]Milking Order G
题面
存在 $ n $ 头犇,你需要给所有犇挤奶,给定 $ m $ 条限制,每条限制有序列 $ c_{n'} $,表示犇 $ c_i $ 需要在 $ c_{i + 1} $ 之前被挤奶。你需要在满足前 $ k $ 条限制的条件下求出字典序最小的给所有犇挤奶的顺序序列。最大化 $ k $ 并输出此时字典序最小的挤奶序列。
$ 1 \le n \le 10^5, 1 \le m \le 5 \times 10^4, 1 \le \sum n' \le 2 \times 10^5 $。
Examples
Input_1
4 3 3 1 2 3 2 4 2 3 3 4 1
Output_1
1 4 2 3
Solution
首先这个题意二分答案应该很显然吧?二分 $ k $ 然后考虑验证。显然我们每次挤奶的时候是应该选择不需要在任意犇之后挤奶的犇,这东西不难想到,把每个关系抽象成先挤奶的向后挤奶的连有向边,这样每次找的就是入度为 $ 0 $ 的犇,也就是拓朴排序。如果排到最后发现有环路了,那么显然说明矛盾,否则记录一下当前答案为局部最优解。然后注意需要输出字典序最小的,那么我们就把拓朴排序的时候的队列改成优先队列即可。最终复杂度 $ O((n + \sum n') \log m) $。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N, M;
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[210000];
static Edge* P = ed;
Edge* head[110000];
void* Edge::operator new(size_t){return P++;}
void Clear(void){
P = ed;
memset(head, 0, sizeof(Edge*) * (N + 10));
}
int ind[110000];
vector < int > rnk[51000];
vector < int > ans;
vector < int > tmp;
bool Check(int lim){
memset(ind, 0, sizeof(int) * (N + 10));
Clear();
tmp.clear();
for(int i = 1; i <= lim; ++i){
auto lst = rnk[i].begin();
for(auto it = next(rnk[i].begin()); it != rnk[i].end(); ++it)
++ind[*it], head[*lst] = new Edge{head[*lst], *it}, lst = it;
}
std::priority_queue < int, vector < int >, greater < int > > cur;
for(int i = 1; i <= N; ++i)if(!ind[i])cur.push(i);
while(!cur.empty()){
int tp = cur.top(); cur.pop();
tmp.emplace_back(tp);
for(auto i = head[tp]; i; i = i->nxt){
--ind[SON];
if(!ind[SON])cur.push(SON);
}
}
return (int)tmp.size() == N;
}
int main(){
N = read(), M = read();
for(int i = 1; i <= M; ++i){
int m = read();
while(m--)rnk[i].emplace_back(read());
}
int l = 1, r = M;
while(l <= r){
int mid = (l + r) >> 1;
if(Check(mid))ans.swap(tmp), l = mid + 1;
else r = mid - 1;
}
for(auto i : ans)printf("%d ", i);
printf("\n");
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4377 [USACO18OPEN] Talent Show G
题面
给定 $ n $ 头牛存在重量 $ w_i $ 和才艺水平 $ t_i $,给定重量限制 $ W $,要求选出一些牛使得在 $ \sum w_i \ge W $ 的条件下最大化 $ \dfrac{\sum t_i}{\sum w_i} $,具体地,输出最大化后的 $ \lfloor ans \times 10^3 \rfloor $。
$ 1 \le n \le 250, 1 \le W \le 10^3, 1 \le w_i \le 10^6, 1 \le t_i \le 10^3 $,保证 $ \sum_{i = 1}^n w_i \ge W $。
Examples
Input_1
3 15 20 21 10 11 30 31
Output_1
1066
Solution
完全可以算是 01分数规划 的板子了,然后再套个 01背包即可。具体地,通过 01分数规划,转化一下有 $ \sum t_i - ans \times \sum w_i \ge 0 $,二分 $ ans $,然后验证通过 01背包 实现,让价值 $ c_i = t_i - ans \times w_i $,对于 $ j + w_i \ge W $ 直接转化到 $ dp(W) $,最后判断一下 $ dp(W) $ 是否大于等于 $ 0 $ 即可。注意边界 $ dp(0) = 0 $ 和枚举 $ W $ 的那一维需要到 $ 0 $。最终复杂度没算错的话大概是 $ O(nW \log(\sum t_i \times eps^{-1})) $,也就是 $ 2e5 \times \log 2e9 $。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define EPS (double)(1e-7)
template< typename T = int >
inline T read(void);
int N, W;
int wei[300], val[300];
double c[300];
double dp[1100];
bool Check(double lim){
for(int i = 1; i <= 1010; ++i)dp[i] = -114514.0;
for(int i = 1; i <= N; ++i)c[i] = (double)val[i] - lim * (double)wei[i];
for(int i = 1; i <= N; ++i)for(int j = W; j >= 0; --j)
j + wei[i] >= W
? dp[W] = max(dp[W], dp[j] + c[i])
: dp[j + wei[i]] = max(dp[j + wei[i]], dp[j] + c[i]);
return dp[W] >= 0.0;
}
int main(){
N = read(), W = read();
double l(0.0), r(0.0);
for(int i = 1; i <= N; ++i)wei[i] = read(), val[i] = read(), r += (double)val[i];
int ans;
while(l + EPS <= r){
double mid = (l + r) / 2.0;
if(Check(mid))ans = (int)floor(mid * 1000.0), l = mid;
else r = mid;
}printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4378 [USACO18OPEN]Out of Sorts S
题面
给定你冒泡排序的 “奶牛码” 实现,特别地,定义语句 moo 为输出 moo,对于给定的序列求该 “奶牛码” 会输出几次 moo。
sorted = false
while (not sorted):
sorted = true
moo
for i = 0 to N-2:
if A[i+1] < A[i]:
swap A[i], A[i+1]
sorted = false
$ 1 \le n \le 10^5, 1 \le a_i \le 10^9 $。
Examples
Input_1
5 1 5 3 8 2
Output_1
4
Solution
离散化,树状数组求逆序对个数,没了。确实没了,分没了。。。
放学前五分钟糊了一个 BIT + 离散化然后交上去直接 WA,回来扫了一眼题目才发现我是**。
观察发现这玩意不是在每次交换的时候 moo,而是每一趟尝试交换的时候叫一下。那么这东西就需要考虑一下冒泡排序的本质了,发现冒泡排序每次都是扫一遍给所有数的逆序对减少一个,这个应该比较好理解吧,每扫一遍的过程可以认为是把某些数往后移动一段,每次移动都会把这个数对跨过的这段数的 $ 1 $ 的贡献抵消,也就是减少一个逆序对。那么我们的答案就是对于每一位数,最大的逆序对个数然后再 $ +1 $,最后的加一是因为即使有序了也还要再跑一边判断。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
int a[110000];
vector < int > data;
class BIT{
private:
int tr[110000];
public:
int lowbit(int x){return x & -x;}
void Modify(int x, int v = 1){while(x <= N)tr[x] += v, x += lowbit(x);}
int Query(int x){int ret(0); while(x)ret += tr[x], x -= lowbit(x); return ret;}
}bit;
int main(){
N = read();
for(int i = 1; i <= N; ++i)a[i] = read(), data.emplace_back(a[i]);
sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
for(int i = 1; i <= N; ++i)a[i] = (int)data.size() - distance(data.begin(), lower_bound(data.begin(), data.end(), a[i]) + 1) + 1;
int ans(0);
for(int i = 1; i <= N; ++i)ans = max(ans, bit.Query(a[i] - 1)), bit.Modify(a[i]);
printf("%d\n", ans + 1);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4375 [USACO18OPEN]Out of Sorts G
题面
与上题题意及范围不变,奶牛码变成如下:
sorted = false
while (not sorted):
sorted = true
moo
for i = 0 to N-2:
if A[i+1] < A[i]:
swap A[i], A[i+1]
for i = N-2 downto 0:
if A[i+1] < A[i]:
swap A[i], A[i+1]
for i = 0 to N-2:
if A[i+1] < A[i]:
sorted = false
Examples
Input_1
5 1 8 5 3 2
Output_1
2
Solution
可以尝试不用 BIT。。可以用 Treap,可以用 LCT。。
考虑和上一题有何不同,上一题是每个数之前的数对其贡献的逆序对取 $ \max $,因为每次会把数前面的一个大于它的数移到其之后。考虑本题,不难想到每次先把一个大于它的丢到之后,再把一个小于它的丢到之前,考虑对于一个具体的有序的位置 $ i $,不难想到是每次从 $ [1, i] $ 中丢出去一个不属于这段里的并且同时丢进来一个属于这段的,也就是说位置 $ i $ 的答案就是 $ [1, i] $ 中不符合的数量(注意这里的位置是在排序之后的有序位置)。所以本题和位置相关,我们把权值排个序,然后丢下标进 BIT 求逆序对即可。记得答案需要和 $ 1 $ 取 $ \max $。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
pair < int, int > a[110000];
class BIT{
private:
int tr[110000];
public:
int lowbit(int x){return x & -x;}
void Modify(int x, int v = 1){while(x <= N)tr[x] += v, x += lowbit(x);}
int Query(int x){int ret(0); while(x)ret += tr[x], x -= lowbit(x); return ret;}
}bit;
int main(){
N = read();
int ans(1);
for(int i = 1; i <= N; ++i)a[i] = {read(), i};
sort(a + 1, a + N + 1);
for(int i = 1; i <= N; ++i)
bit.Modify(a[i].second),
ans = max(ans, i - bit.Query(i));
printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4372 [USACO18OPEN]Out of Sorts P
题面
存在一个奇怪的快速排序,大致过程是每次通过冒泡排序找到分割点,定义分割点为其左侧的数均小于它,右侧均大于它。找到分割点之后将原序列分割并递归处理被分出来的序列。求最终 work_counter 的值。
主程序奶牛码为:
quickish_sort (A) {
if length(A) = 1, return
do { // Main loop
work_counter = work_counter + length(A)
bubble_sort_pass(A)
} while (no partition points exist in A)
divide A at all partition points; recursively quickish_sort each piece
}
对于冒泡排序为:
bubble_sort_pass (A) {
for i = 0 to length(A)-2
if A[i] > A[i+1], swap A[i] and A[i+1]
}
Examples
Input_1
7 20 2 3 4 9 8 7
Output_1
12
Solution
不难发现题意就是要我们求每次冒泡排序的长度求和,然后发现这东西也不太好求,于是再次转化为求每个数进行了多少次冒泡排序,次数求和显然也是原来的值。不难想到,对于一个数,其不会再被进行冒泡排序当且仅当其左右两个数均为分割点,所以我们的问题就再次转化为求每个点在几次冒泡排序后才会变成分割点,令其为 $ tim_i $,那么答案就是 $ \sum_{i = 1}^n \max(tim_i, tim_{i - 1}) $。
考虑维护这玩意,不难想到,每次冒泡排序都会把这个数相对所有其后面的小于它的数的距离减 $ 1 $,所以答案也就是距离其最远的那个不合法的位置和这个数的位置的距离,记得和 $ 1 $ 取 $ \max $。
对于具体的维护方式用单调队列或者双指针之类的东西弄一下即可,注意需要离散化,且这个离散化和掉进兔子洞那题差不多,对于相同的值离散化之后的值应该是不同的,这样我们直接倒序遍历,然后维护一个指针,指向第一个满足 $ a_i \lt i $ 的,求个距离即为答案。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
int a[110000];
vector < int > data;
int tim[110000];
int cnt[110000];
int main(){
N = read();
for(int i = 1; i <= N; ++i)data.emplace_back(a[i] = read());
sort(data.begin(), data.end()); //data.erase(unique(data.begin(), data.end()), data.end());
for(int i = 1; i <= N; ++i)a[i] = distance(data.begin(), lower_bound(data.begin(), data.end(), a[i]) + 1), a[i] += cnt[a[i]]++;
int lst(N);
for(int i = N; i >= 1; --i){
while(a[lst] > i)--lst;
tim[i] = max(lst - i, 1);
}ll ans(0);
for(int i = 1; i <= N; ++i)ans += max(tim[i - 1], tim[i]);
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4374 [USACO18OPEN]Disruption P
题面
给定一棵 $ n $ 节点无权树,额外地,给定 $ m $ 条有权无向边,连结在 $ n $ 个节点之间。对于原始的树上 $ n - 1 $ 条边的每一条,求出若删去这条边,添加 $ m $ 条额外边的哪一条可以在使树再次连通的基础上最小化权值,求该权值。
$ 2 \le n, m \le 5 \times 10^4 $。
Examples
Input_1
6 3 1 2 1 3 4 1 4 5 6 5 2 3 7 3 6 8 6 4 5
Output_1
7 7 8 5 5
Solution
依然在题解里先偷个图。。
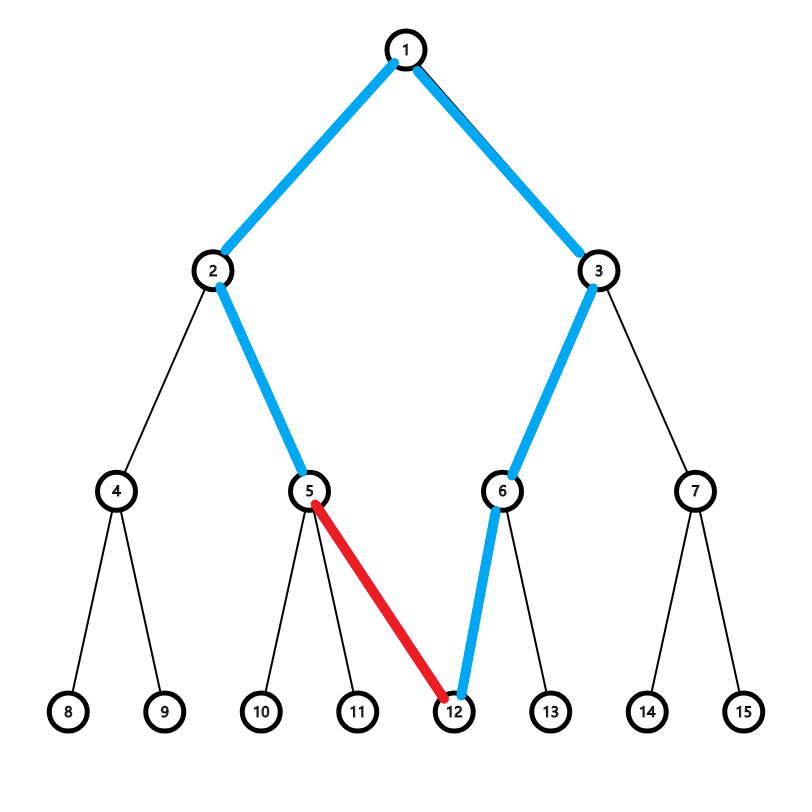
显然考虑对于我们每一条连的额外边,如 $ 5 \Longleftrightarrow 12 $,显然只会对树上两点之间的路径上的边产生贡献,这个比较容易想吧。。随便画一下就好,比如显然如果把原树上非该路径上的边删掉,即使连上这条额外边也无济于事。然后对于某一条原树边,显然答案就是所有贡献取个 $ \min $。说到这一个最显而易见的做法已经出来了,树剖转成序列,然后线段树上求区间 $ \min $。
然后我们发现,如果把额外边降序排序,显然后面的边更优,那么每次操作实际上就是覆盖原来的值,那么这东西很显然就是个 assign,而且只有 assign 没有任何其它操作,所以可以考虑直接上个 树剖 + ODT 即可,理论上对于只有 assign 的操作 ODT 应该更快,但是可能常数太大了,所以最终表现似乎不如线段树?
然后在此之上,我们又可以想到一个做法,把额外边升序排列,这样前面的一定更优,打个标记,对于已经更新过的不去更新即可,然后用倍增或者 Tarjan 直接的求 LCA 找树上路径之类的,可以省掉一个树剖。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
struct Edge{
Edge* nxt;
int to;
int idx;
OPNEW;
}ed[110000];
ROPNEW(ed);
Edge* head[51000];
int ans[51000], nod_idx[51000];
int N, M;
int dep[51000], dfn[51000], idx[51000], top[51000], siz[51000], fa[51000], hson[51000];
struct Node{
int l, r;
mutable int val;
friend const bool operator < (const Node &a, const Node &b){
return a.l < b.l;
}
};
class ODT{
private:
set < Node > tr;
public:
auto Insert(Node x){return tr.insert(x);}
auto Split(int p){
auto it = tr.lower_bound(Node{p});
if(it != tr.end() && it->l == p)return it;
--it;
// printf("%d %d %d\n", it->l, it->r, it->val);
int l = it->l, r = it->r, v = it->val;
tr.erase(it), Insert(Node{l, p - 1, v});
return Insert(Node{p, r, v}).first;
}
void Assign(int l, int r, int v){
if(l > r)return;
// printf("assigning %d~%d, %d\n", l, r, v);
auto itR = Split(r + 1), itL = Split(l);
tr.erase(itL, itR);
Insert(Node{l, r, v});
}
void SetAns(void){
for(auto nod : tr)
for(int i = nod.l; i <= nod.r; ++i)
ans[nod_idx[idx[i]]] = nod.val;
}
}odt;
struct Edges{
int s, t;
int val;
friend const bool operator < (const Edges &a, const Edges &b){
return a.val > b.val;
}
};
vector < Edges > es;
void dfs_pre(int p = 1, int ffa = 0){
fa[p] = ffa;
dep[p] = dep[ffa] + 1;
siz[p] = 1;
for(auto i = head[p]; i; i = i->nxt){
if(SON == ffa)continue;
nod_idx[SON] = i->idx;
dfs_pre(SON, p);
siz[p] += siz[SON];
if(siz[SON] > siz[hson[p]])hson[p] = SON;
}
}
void dfs(int p = 1, int tp = 1){
static int cdfn(0);
top[p] = tp;
dfn[p] = ++cdfn;
idx[cdfn] = p;
if(hson[p])dfs(hson[p], tp);
for(auto i = head[p]; i; i = i->nxt){
if(SON == fa[p] || SON == hson[p])continue;
dfs(SON, SON);
}
}
void AssignRange(int s, int t, int val){
while(top[s] != top[t]){
if(dep[top[s]] < dep[top[t]])swap(s, t);
odt.Assign(dfn[top[s]], dfn[s], val);
s = fa[top[s]];
}if(dep[s] < dep[t])swap(s, t);
odt.Assign(dfn[t] + 1, dfn[s], val);
}
int main(){
N = read(), M = read();
for(int i = 1; i <= N - 1; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t, i};
head[t] = new Edge{head[t], s, i};
}dfs_pre(), dfs();
// for(int i = 1; i <= N; ++i)printf("[%d]: dfn: %d, fa: %d, dep: %d, top: %d, hson: %d\n", i, dfn[i], fa[i], dep[i], top[i], hson[i]);
// for(int i = 1; i <= N; ++i)printf("nodidx[%d]: %d\n", i, nod_idx[i]);
odt.Insert(Node{1, N, -1});
for(int i = 1; i <= M; ++i){
int s = read(), t = read(), v = read();
es.emplace_back(Edges{s, t, v});
}sort(es.begin(), es.end());
for(auto e : es)AssignRange(e.s, e.t, e.val);
odt.SetAns();
for(int i = 1; i <= N - 1; ++i)printf("%d\n", ans[i]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4373 [USACO18OPEN]Train Tracking P
题面
给定长度为 $ n $ 的序列 $ c_n $,按序求出其中每段长度为 $ k $ 的子串中的最小值。特别地,整个过程中在全局你只能使用一个长度为 $ 5.5 \times 10^3 $ 的 int 类型静态数组,且存取次数和不能超过 $ 2.5 \times 10^7 $ 次,仅在处理序列中单独某个数时,或者说在 helpBessie() 中对于局部变量无空间限制,且你可以获取 $ 2 $ 次整个序列。
题目通过交互实现,具体地,对于序列中每个值都会调用一次 helpBessie(),你需要实现该函数,函数中对于局部非静态变量空间无限制(或者说 256MiB),在函数中你可以通过调用交互库来获取本次的基本信息和存取数,即禁止使用静态变量或全局变量。对于具体的实现方式请参考 原题面。
$ 1 \le k \le n \le 10^6, 1 \le c_i \le 10^9 $。
Examples
Input_1
10 3 5 7 9 2 0 1 7 4 3 6
Output_1
5 2 0 0 0 1 3 3
Tips:输入输出不代表交互过程。
Solution
显然如果没有空间的限制的话我们直接写个滑动窗口,或者说单调队列即可很简单的求解。但是发现这个单调队列的空间是 $ O(n) $ 的肯定存不下,然后看一下空间的大小,发现空间限制是 $ O(\sqrt{n}) $ 的,于是不难想到分块实现。
因为我们一共可以获取两次序列的值,所以可以考虑先将序列分成 $ \sqrt{n} $ 块,然后在第一次的时候对于每一块维护一个。。。
然后先跳了,没啥好题解,仅有的两个中文题解没能太明白,代码也没看懂,如果 NOIP 没退役的话就回来补这题。。
Tips:对于交互题的调试,我们实际上可以将交互库中的函数手动模拟实现,然后写个主函数调用对应的函数 “模拟” 一遍交互的过程,然后对比结果。如 void set(int index, int value){a[index] = val;}。
Code
//TODO
UPD
update-2022_11_15 初稿


 浙公网安备 33010602011771号
浙公网安备 33010602011771号