[ABC248F] Keep Connect 题解

[ABC248F] Keep Connect Solution

目录

• [ABC248F] Keep Connect Solution
  • 更好的阅读体验戳此进入
  • 题面
  • Solution
  • Code
  • UPD

更好的阅读体验戳此进入

题面

给定 $ n, p $，存在如图的 $ 2 \times n $ 的网格图，显然初始共有 $ 2n $ 个顶点和 $ 3n - 2 $ 条边，分别求删除 $ i \in [1, n - 1] $ 条边后仍使图连通的删边方案数，对 $ p $ 取模。

Solution

这种题 DP 很显然，考虑设状态 $ dp(i, j, 0/1) $ 表示考虑前 $ i $ 列，删除了 $ j $ 条边，第 $ i $ 列上下两点之间是否连边，然后对不同情况无脑进行分类讨论即可。

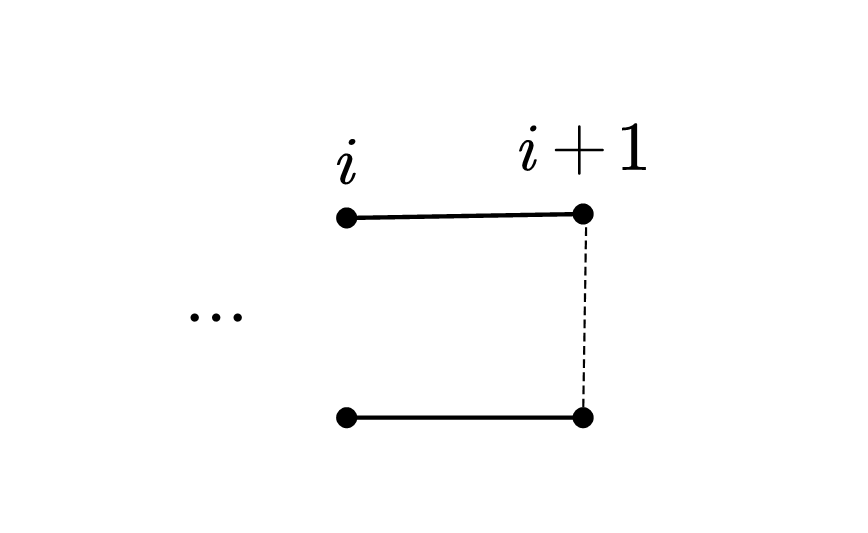
具体地，对于 $ dp(i, j, 0) $，如下图，此时 $ i $ 位置两个点竖直方向并未连边，则为了保证连通性，那么 $ i $ 到 $ i + 1 $ 的水平的两个边必须连上，而 $ i + 1 $ 的竖直的边（即虚线边）是否连结均合法，则有如下转移：

\[\begin{aligned} &dp(i, j, 0) \longrightarrow dp(i + 1, j + 1, 0) \\ &dp(i, j, 0) \longrightarrow dp(i + 1, j, 1) \end{aligned} \]

对于 $ dp(i, j, 1) $，如下图，三条边都不能直接确定，所以需要继续讨论，具体地，可以讨论 $ i + 1 $ 的竖直边是否连结，简单想一下就有如下 $ 4 $ 个转移，此处不多赘述，直接看方程吧。

\[\begin{aligned} &dp(i, j, 1) \times 2 \longrightarrow dp(i + 1, j + 1, 1) \\ &dp(i, j, 1) \longrightarrow dp(i + 1, j, 1) \\ &dp(i, j, 1) \times 2 \longrightarrow dp(i + 1, j + 2, 0) \\ &dp(i, j, 1) \longrightarrow dp(i + 1, j + 1, 1) \end{aligned} \]

同时注意 $ \times 2 $ 是因为要枚举上下的两个水平边删掉其中一个。

边界可以是 $ dp(1, 0, 1) = dp(1, 1, 0) = 1 $，对应删边数 $ d $ 的答案即为 $ dp(n, d, 1) $。

Code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template< typename T = int >
inline T read(void);

int N; int MOD;
int dp[3100][3100][2];

int main(){
    N = read(), MOD = read();
    dp[1][0][1] = dp[1][1][0] = 1;
    for(int i = 1; i <= N - 1; ++i)
        for(int j = 0; j <= N - 1; ++j)
            dp[i + 1][j + 1][0] = ((ll)dp[i + 1][j + 1][0] + dp[i][j][0]) % MOD,
            dp[i + 1][j][1] = ((ll)dp[i + 1][j][1] + dp[i][j][0]) % MOD,
            dp[i + 1][j + 1][1] = ((ll)dp[i + 1][j + 1][1] + dp[i][j][1] * 2ll) % MOD,
            dp[i + 1][j][1] = ((ll)dp[i + 1][j][1] + dp[i][j][1]) % MOD,
            dp[i + 1][j + 2][0] = ((ll)dp[i + 1][j + 2][0] + dp[i][j][1] * 2ll) % MOD,
            dp[i + 1][j + 1][1] = ((ll)dp[i + 1][j + 1][1] + dp[i][j][1]) % MOD;
    for(int i = 1; i <= N - 1; ++i)printf("%d%c", dp[N][i][1], i == N - 1 ? '\n' : ' ');
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    int flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

UPD

update-2022_11_21 初稿