POI 2013 题解(长文警告)
POI 2013 Solution
- POI 2013 Solution
- 更好的阅读体验戳此进入
- 题面链接
- 另一个题面链接
- LG-P3558 [POI2013]BAJ-Bytecomputer
- LG-P3550 [POI2013]TAK-Taxis
- LG-P3560 [POI2013]LAN-Colorful Chain
- LG-P3552 [POI2013]SPA-Walk
- LG-P3556 [POI2013]MOR-Tales of seafaring
- LG-P3563 [POI2013]POL-Polarization
- LG-P3551 [POI2013]USU-Take-out
- LG-P3553 [POI2013]INS-Inspector
- LG-P3557 [POI2013]GRA-Tower Defense Game
- LG-P3554 [POI2013]LUK-Triumphal arch
- LG-P3547 [POI2013]CEN-Price List
- LG-P3562 [POI2013] LAS-Laser
- LG-P3548 [POI2013] GOB-Tapestries
- LG-P3559 [POI2013] LAB-Maze
- LG-P3549 [POI2013]MUL-Multidrink
- UPD
更好的阅读体验戳此进入
(建议您从上方链接进入我的个人网站查看此 Blog,在 Luogu 中图片会被墙掉,部分 Markdown 也会失效)
题面链接
另一个题面链接
LG-P3558 [POI2013]BAJ-Bytecomputer
题面
给定长度为 $ n $ 的仅包含 $ -1, 0, 1 $ 的数列,每次操作可以使 $ a_i \leftarrow a_i + a_{i - 1} $,求最少操作次数使序列单调不降,无解输出 BRAK。
$ n \le 10^6 $。
Examples
Input_1
6 -1 1 0 -1 0 1
Output_1
3
Solution
一道绿色但我感觉还挺有意思的 DP。
这个数据范围这个题意,是一道 DP 应该很显然吧。。。
首先我们可以贪心地想到,为了使操作次数尽可能地少,最终操作完的数列应该还是均为 $ -1, 0, 1 $。
然后我们就可以考虑设置状态 $ dp(i)(j) $,表示考虑前 $ i $ 个数,形成以 $ j $ 结尾的合法数列需要的操作数。
然后分类讨论第 $ i $ 个数是什么,分别进行转移,这个应该很显然,对吧?
switch(a[i]){
case -1:{
dp[i][-1] = dp[i - 1][-1];
// dp[i][0] = dp[i - 1][1] + 1;
dp[i][1] = dp[i - 1][1] + 2;
break;
}
case 0:{
dp[i][-1] = dp[i - 1][-1] + 1;
dp[i][0] = min(dp[i - 1][-1], dp[i - 1][0]);
dp[i][1] = dp[i - 1][1] + 1;
break;
}
case 1:{
dp[i][-1] = dp[i - 1][-1] + 2;
dp[i][0] = dp[i - 1][-1] + 1;
dp[i][1] = min({dp[i - 1][-1], dp[i - 1][0], dp[i - 1][1]});
break;
}
default:break;
}
然后聪明的你发现按照一般思路写完无法 Accept,甚至样例都过不了,简单分析一下发现,对于 Case -1 的第二行的转移显然是不合法的。
思考这个转移的含义是什么,原数列上第 $ i $ 位是 $ -1 $,我们想要将其变为 $ 0 $,而这需要让第 $ i - 1 $ 位为 $ 1 $,用 $ 1 $ 来操作第 $ i $ 位的 $ -1 \(,这个时候我们就已经可以发现问题了:\) 1, 0 $ 这个已经不符合单调不降的规则了,所以这个转移是不合法的,注释掉之后直接 Accept。
Tips:对于一些空间上的优化,可以考虑通过类似背包问题二维压一维的滚动数组的优化,不过意义不大,然后为了写起来更直观,需要让数组支持访问负下标,可以写成如下形式:
int dp_r[1100000][4];
int* dp[1100000];
然后主函数里这样初始化:
memset(dp_r, 0x3f, sizeof(dp_r));
for(int i = 0; i <= 1010000; ++i)dp[i] = dp_r[i] + 1;
大概就这样。。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define INF 0x3f3f3f3f
template<typename T = int>
inline T read(void);
int N;
int a[1100000];
int dp_r[1100000][4];
int* dp[1100000];
int main(){
memset(dp_r, 0x3f, sizeof(dp_r));
for(int i = 0; i <= 1010000; ++i)dp[i] = dp_r[i] + 1;
N = read();
for(int i = 1; i <= N; ++i)a[i] = read();
dp[1][a[1]] = 0;
for(int i = 2; i <= N; ++i){
switch(a[i]){
case -1:{
dp[i][-1] = dp[i - 1][-1];
// dp[i][0] = dp[i - 1][1] + 1;
dp[i][1] = dp[i - 1][1] + 2;
break;
}
case 0:{
dp[i][-1] = dp[i - 1][-1] + 1;
dp[i][0] = min(dp[i - 1][-1], dp[i - 1][0]);
dp[i][1] = dp[i - 1][1] + 1;
break;
}
case 1:{
dp[i][-1] = dp[i - 1][-1] + 2;
dp[i][0] = dp[i - 1][-1] + 1;
dp[i][1] = min({dp[i - 1][-1], dp[i - 1][0], dp[i - 1][1]});
break;
}
default:break;
}
}
// for(int i = 1; i <= N; ++i){
// for(int j = -1; j <= 1; ++j){
// printf("%d%c", dp[i][j], j == 1 ? '\n' : ' ');
// }
// }
int ans = min({dp[N][-1], dp[N][0], dp[N][1]});
ans >= INF ? printf("BRAK\n")
: printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3550 [POI2013]TAK-Taxis
题面
存在一条线段,有三个位置,$ 0 \((即原点)为 Byteasar 初始所在的位置,\) d $ 为出租车总部位置,$ m $ 为目的地位置,有 $ n $ 辆出租车,每辆出租车都有一个行驶路程上限 $ x_i $,每辆出租车都从总部出发,并且最终可以不回到总部。Byteasar 能搭乘出租车行动,但是他可以在任意时刻任意点改变出租车。
求最少需要多少辆出租车才能使 Byteasar 抵达目的地,无解输出 $ 0 $。
$ 1 \le d \le m \le 10^{18}, 1 \le n \le 5 \times 10^5, 1 \le x_i \le 10^{18} $。
输入格式
$ m $ $ d $ $ n $
$ x_1, x_2, \cdots, x_n $
Examples
Input_1
42 23 6 20 25 14 27 30 7
Output_1
4
Solution
本来看这题面感觉很像一道 DP,然后口糊了半天也没想到什么优秀的状态和转移。。。
所以这道题是个贪心。
大概就是显然每辆车是需要先先走到人所在的位置然后向着总部走,这个过程我们可以考虑到显然优先选路程上限更大的车是更优的,这个很显然吧,如果选路程小的那么去掉前往人所在位置的路程,最终的贡献就会更小,会导致后面的车无用的路程更多,贡献也会变小。
但如果只考虑这样可能会导致因为前面为了解更优而耗费了过多的大车导致最终只剩下路程小于 $ m - d $ 的小车,从而使有解变为无解,所以我们需要为最后的 $ m - d $ 的路程预留一个路程最短但 $ x_i \ge m - d $ 的车,然后按照刚才的思路贪心。
然后贪心是正确的,但我的之前证明假了。。
update:
考虑对于最后一段 $ m - d $ 的路程一定是需要通过一辆至少为 $ m - d $ 的车来送走的,于是我们预留下车之后,设预留的车为 $ \xi $,且 $ \xi \ge m - d $,剩下的车我们按照从大到小贪心地使用,那么如果最后一辆车可以在到达 $ d $ 以前直接送到 $ m $,那么显然设这辆车为 $ \epsilon $,设车 $ \epsilon $ 需要向 $ 0 $ 走的路程为 $ \alpha $,那么一定满足 $ \epsilon \ge \alpha \times 2 + m - d $ 且 $ \xi \le \epsilon $,这样显然我们完全不需要用预留的 $ \xi $ 这辆车。
如果最后一辆车不能送到终点,那么在有解的情况下一定至少都再需要一辆大于 $ m - d $ 的车,那么按照我们的贪心思路选择最小的大于 $ m - d $ 的车一定是最优的,或者说不劣的,$ \square $。
下面的内容均为之前写的假的证明,思路错了,这里留作纪念。
这时候仔细想一下就会发现一个问题,如果我们在到达总部之前的,乘坐的最后一辆车的行驶距离足够长,可以把我们送到超过总部 $ \xi $ 距离的位置,那么这个时候我们就只需要 $ x_i \ge m - d - \xi $ 的车就可以达到目标,那么有没有可能因为我们最初预留的那辆车距离过长而导致答案更劣?
我们可以考虑令按照贪心策略预留的车距离为 $ \alpha $,令在到达总部之前选择的所有车距离的最小值为 $ \beta $,令走到总部前倒数第二辆车到达的位置距离总部的位置为 $ \epsilon $。
显然如果 $ \beta \ge 2 \times \epsilon + (m - d) $,那么到达总部前的最后一辆车就已经可以带我们走到目的地,那么预留的车便可以无需使用,答案减少 $ 1 $。
反之则为一般情况:
若 $ \beta \ge \alpha $:那么显然需要使用预留的车。
若 $ \beta \lt \alpha $:此时我们可能会认为将 $ \alpha, \beta $ 互换,或者说将 $ \alpha $ 变为一个更小一点的车,会令结果更优,但是仔细思考一下就会发现,因为此时显然因为 $ \beta \lt 2 \times \epsilon + (m - d) $,所以即使改变 $ \alpha $,也只能使到达总部前的最后一辆车到达超过总部比 $ \xi $ 更远的位置,依然不能直接到达 $ m $,所以此时是改变 $ \alpha $,只会使方案改变,而不会使最少使用的车辆数改变,最终仍然需要额外的一辆车来送到最终的目的地。
同时注意,上述我们论述的均为到达总部前最后一辆车能将我们送到超过总部的位置,如果最后一辆车无法将我们送达总部,我们也不能直接判定为无解,需要考虑到预留的那辆车也可以先向总部左侧行驶一段后再向右行驶到目的地,所以在跳出循环之后还需要判断一下。
因此在程序中我们除了判定是否满足到达 $ m $ 之外,也需要判断是否到达了可以直接使用预留的车辆送达目的地的位置,如果到了就直接输出 $ ans + 1 $ 即可。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define int ll
template<typename T = int>
inline T read(void);
int M, D, N;
vector < int > dis;
signed main(){
// freopen("in.txt", "r", stdin);
M = read(), D = read(), N = read();
for(int i = 1; i <= N; ++i)dis.push_back(read());
sort(dis.begin(), dis.end(), greater < int >());
auto ptr = lower_bound(dis.rbegin(), dis.rend(), M - D);
if(ptr == dis.rend()){printf("0\n"); return 0;}
int val = *ptr;
dis.erase((++ptr).base());
int cur(0), ans(0);
for(auto i : dis){
cur += i - (D - cur);
++ans;
if(cur <= 0){--ans; break;}
if(cur >= M){printf("%lld\n", ans); return 0;}
if(cur >= D - (val - (M - D)) / 2){printf("%lld\n", ans + 1); return 0;}
// printf("cur:%d, ans:%d\n", cur, ans);
}
if((D - cur) * 2 + (M - D) <= val)printf("%lld\n", ans + 1);
else printf("0\n");
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3560 [POI2013]LAN-Colorful Chain
题面
这道题的难度就难在理解洛谷的阴间翻译
给定长度为 $ n $ 的序列 $ a_1, a_2, \cdots, a_n $,有 $ m $ 个限制,每个限制为 $ c_i, l_i $,求该序列有多少个子串,满足:
每个 $ c_i $ 在子串中出现且仅出现了 $ l_i $ 次,且不存在其它的数。
$ 1 \le n, m \le 10^6 \(,\) c_i $ 互不相同,过程中所有数均满足在 int 范围内。
输入格式
$ n $ $ m $
$ l_1, l_2, \cdots, l_m $
$ c_1, c_2, \cdots, c_m $
$ a_1, a_2, \cdots, a_n $
Examples
Input_1
7 3 2 1 1 1 2 3 4 2 1 3 1 2 5
Output_1
2
Solution
很水的一道题。。。
显然符合要求的字串的长度一定为 $ \sum_{i = 1}^{m} l_i $。
写个滑动窗口,记录一下当前窗口内有多少符合要求的数,和 $ \sum_{i = 1}^{m} l_i $ 相同的话答案 $ +1 $,用 unordered_map 记录一下每个数在窗口内出现了几次,然后每次移动分类讨论一下符合要求的数是否变化,复杂度 $ O(n) $ 解决。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
stms => sum_times
ctms => current_times
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
int N, M;
unordered_map < int, int > seq;
int tms[1100000];
int ctms(0);
int stms(0);
int a[1100000];
int ans(0);
int main(){
N = read(), M = read();
int tmp[1100000];
for(int i = 1; i <= M; ++i)tmp[i] = read(), stms += tmp[i];
for(int i = 1; i <= M; ++i)tms[read()] = tmp[i];
for(int i = 1; i <= N; ++i)a[i] = read();
for(int i = 1; i <= stms; ++i){
if(seq.find(a[i]) != seq.end())seq[a[i]]++;
else seq.insert({a[i], 1});
if(seq[a[i]] <= tms[a[i]])++ctms;
}
if(ctms == stms)++ans;
for(int i = stms + 1; i <= N; ++i){
int tail = i - stms;
if(seq[a[tail]] <= tms[a[tail]])--ctms;
seq[a[tail]]--;
if(seq.find(a[i]) != seq.end()){
if(seq[a[i]] < tms[a[i]])++ctms;
seq[a[i]]++;
}else{
if(tms[a[i]])++ctms;
seq.insert({a[i], 1});
}
if(ctms == stms)++ans;
}
printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3552 [POI2013]SPA-Walk
题面
存在 $ 2^n $ 个长度为 $ n $ 的 $ 01 $ 串,两个 $ 01 $ 串之间有边当且仅当两者之间仅有一位不同,或者说 $ x, y $ 之间有边当且仅当 $ x \oplus y = 2^t $。我们称这样的一个图为 $ n $ 维超立方体(n-dimensional hipercube)。现在从这其中去掉 $ k $ 个串 $ s_1, s_2, \cdots, s_k $,给定两个串 $ S, T $,求两者之间是否能够到达。
能到达输出 TAK,反之输出 NIE。
$ 1 \le n \le 60, 0 \le k \le \min(10^6, 2^n - 1), n \times k \le 5 \times 10^6 $。
输入格式
$ n \quad k $
$ S \quad T $
$ s_1 $
$ s_2 $
$ \cdots $
$ s_k $
(偷个懒就不写文字叙述了。。。)
Examples
Input_1
4 6 0000 1011 0110 0111 0011 1101 1010 1001
Output_1
TAK
Solution
这道题我本来还以为是和 LG-P7966 [COCI2021-2022#2] Hiperkocka 差不多的题,该题题解,按照那道题的思路想了一下然后假了,改了一下之后 T 掉了,寄,和之前的题关系不是很大,只是定义一样。
Lemma 1:对于一个 $ n $ 维超立方体,令点集为 $ S $,将其所有的点分为两个点集 $ S_1, S_2 \(,\) S_1 \cup S_2 = S, S_1 \cap S2 = \phi $,则两点集之间的边集的大小一定不小于两点集之间较小者的大小,也就是 $ \left\vert { (u, v) \vert u \in S_1, v \in S_2, u \oplus v = 2^t } \right\vert = \min(\left\vert S_1 \right\vert, \left\vert S_2 \right\vert) $。
证明:A proof is left to the reader.
证明:这东西大多数地方都没有人证明,甚至官方题解,感觉可以当成一个已知结论记住,关于严谨证明网上也找到了个大佬的证明(看不懂),戳此进入。
Lemma 2:对于一个 $ n $ 维超立方体,将其删去 $ k $ 个点后,最多仅能够形成 $ 1 $ 个点集大小大于 $ n \times k $ 的连通块。
证明:假设我们现在有两个连通块,其点集分别为 $ S_1, S_2 $,显然 $ S_1 \cap S_2 = \phi $,我们设 $ \left\vert S_1 \right\vert, \left\vert S_2 \right\vert \ge n \times k $,令点的全集为 $ S $,则显然 $ S_2 \subset S \cap \overline{S_1} $。我们又可以通过 Lemma 1 知道 $ S_1 $ 和 $ S \cap \overline{S_1} $ 之间的边集大小不小于 $ \min(\left\vert S_1 \right\vert, \left\vert S \cap \overline{S_1} \right\vert) $,也就是其边集 $ E $ 满足 $ E \ge n \times k + 1 $,也就是说如果我们想要形成这两个连通块就必须要断开至少 $ n \times k + 1 $ 条边,而我们去掉 $ k $ 个点只能断开 $ n \times k $ 条边,无法形成这两个连通块,$ \square $。
于是只要有了 Lemma 2,我们就可以很容易想到,令出发点和终点分别为 $ S, T $,如果两者可以互通,那么他们要么都在唯一的大于 $ n \times k $ 的连通块内,要么在某一个小于等于 $ n \times k $ 的连通块内,所以我们只需要搜至多 $ n \times k $ 的点数,如果两者都不在小于 $ n \times k $ 的连通块中,那么一定同在唯一的大连通块中,反之如果在同一个连通块内那么一定可以被搜到。
于是我们分别从 $ S, T $ 进行爆搜,各自维护一个 unordered_set 记录其所在连通块有哪些点,如果从搜索过程中遇到另一个点了,则两者同在一个小连通块中,直接输出连通然后 exit,如果连通块大小超过 $ n \times k $ 了那么直接标记一下然后 return。两者都搜完后如果两个连通块都超过 $ n \times k $ 了那么一定同在一个大块,反之则一定不在同一个块,不连通。
另外个人建议把二进制转成 long long 再存,否则还会存在一个 hash 的复杂度,虽然我感觉好像嗯搞也能过???
然后写位移的时候记得写成 1ll。
这个的复杂度大概是 $ O(n^2k) $ 级别的,但是常数可能会很大,算上部分常数大概是个 6e8 的复杂度,比较离谱。
然后。。。Luogu 评测记录
unordered_set 寄了,cc_hash_table 寄的更多,经典被卡常,调了亿会怎么 Luogu 上都是两个点 TLE,一个点 MLE,于是开始手搓 hash 挂链,队列之类的,最终终于在 Luogu 上把这破题给卡过去了。。。
update:
然后 sssmzy 提出了一个很人类智慧的遍历方式,可以保证复杂度为 $ O(nk) $,即搜索的时候不会重复地遍历,大概的思路:
这个思路在 sssmzy 实现了之后发现假掉了,寄,仍然需要卡常。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
uex => unexist
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
ll str2ll(char* s, int n){
ll ret(0), base(0);
for(int i = n - 1; i >= 0; --i)
ret += (1ll << (base++)) * (s[i] == '0' ? 0 : 1);
return ret;
}
#define MOD 2737321
struct Edge{
Edge* nxt;
ll val;
OPNEW;
}eData[4145149];
ROPNEW(eData);
Edge* head[2737330];
void clear(void){memset(head, 0, sizeof(head));}
void Add(ll val){
int idx = val % MOD;
head[idx] = new Edge{head[idx], val};
}
bool Check(ll val){
int idx = val % MOD;
for(auto i = head[idx]; i; i = i->nxt)
if(i->val == val)return true;
return false;
}
ll S, T;
int N, K;
ll cur[5100000];
int fnt(0), til(0);
void bfs(ll S, ll T){
fnt = til = 0;
cur[til++] = S;
Add(S);
while(fnt < til){
ll tp = cur[fnt++];
for(int base = 0; base <= N - 1; ++base){
ll val = tp ^ (1ll << base);
if(val == T)printf("TAK\n"), exit(0);
if(Check(val))continue;
else{
Add(val);
cur[til++] = val;
}
}
if(til > N * K)return;
}
printf("NIE\n"); exit(0);
}
char c[65];
vector < ll > values;
int main(){
// freopen("in.txt", "r", stdin);
N = read(), K = read();
scanf("%s", c); S = str2ll(c, N);
scanf("%s", c); T = str2ll(c, N);
if(S == T)printf("TAK\n"), exit(0);
for(int i = 1; i <= K; ++i){
scanf("%s", c); ll tmpp = str2ll(c, N);
values.push_back(tmpp);
}
for(auto i : values)Add(i);
bfs(S, T);
clear();
for(auto i : values)Add(i);
bfs(T, S);
printf("TAK\n");
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3556 [POI2013]MOR-Tales of seafaring
题面
给定一个 $ n $ 个点 $ m $ 条边的无向图,两点之间距离为 $ 1 \(,\) k $ 次询问求点 $ S, T $ 之间是否有长度为 $ d $ 的路径(不要求一定为简单路径)。
如果有输出 TAK,反之输出 NIE。
简单路径:每个点至多只能被访问一次的路径。
$ 2 \le n \le 5 \times 10^3, 1 \le m \le 5 \times 10^3, 1 \le k \le 10^6, 1 \le d \le 2^{31} - 1 $。
输入格式
$ n \quad m \quad k $
Describe the graph. (m lines)
$ S_1 $ $ T_1 $ $ d_1 $
$ S_2 $ $ T_2 $ $ d_2 $
$ \cdots $
$ S_k $ $ T_k $ $ d_k $
Examples
Input_1
8 7 4 1 2 2 3 3 4 5 6 6 7 7 8 8 5 2 3 1 1 4 1 5 5 8 1 8 10
Output_1
TAK NIE TAK NIE
Solution
显然因为不需要为简单路径,所以一个点可以访问多次,又因为点之间距离为 $ 1 $,所以假设到达目标节点的任意路径的距离为 $ \xi $,那么显然所有满足 $ d = \xi + 2 \times t $ 的 $ d $ 都符合题意,到达目的地后在最后一条边往返跑几次即可。
所以我们就可以发现只要 $ \xi $ 的奇偶性和 $ d $ 相同,且 $ \xi \le d $,那么就一定可以达到要求。
所以对于每次询问我们只需要跑一次从 $ S $ 到 $ T $ 的最短路即可,注意此时需要跑一遍走奇数次的最短路 $ \epsilon $ 和走偶数次的最短路 $ \lambda $,判断一下在有最短路的情况下满足 $ d $ 是奇数且 $ d \gt \epsilon $ 或 $ d $ 是偶数且 $ d \gt \lambda $ 那么则符合题意。
发现 $ n, m $ 较小,$ k $ 较大,所以我们可以对于 $ 1, 2, \cdots, n $ 各自跑一遍最短路,然后记录答案即可,类似离线,然后算一下的话会发现开 int 开不下,所以考虑把答案数组开成 short 即可。
然后我们发现这玩意似乎跑不了 Dijkstra,然后 SPFA 的话理论上是可以被卡到 $ O(n^2m) $ 的,但是因为边权为 $ 1 $ 所以复杂度一定为 $ O(nm) $ 可以过。
考虑 bfs 方法,因为距离仅为 $ 1 $,所以跑 $ n $ 次 bfs,来替换最短路算法,考虑拆点,把每个点拆成 $ x $ 和 $ x + n $,分别表示偶数距离的点和奇数距离的点,然后存图的时候对于 $ (S, T + n), (T, S + n) $ 分别双向存边,这样搜索里的每一步都会走到奇偶性相反的点上以保证正确性,输出答案的时候记录一下即可。这样最后的复杂度是 $ O(nm) $,显然是正确的。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}eData[21000];
ROPNEW(eData);
Edge* head[11000];
int N, M, K;
short dis[10100][10100];
bool vis[10100];
queue < int > q;
void bfs(int S){
memset(vis, false, sizeof(vis));
q.push(S);
// vis[S] = true;
while(!q.empty()){
int tp = q.front(); q.pop();
for(auto i = head[tp]; i; i = i->nxt){
if(vis[SON])continue;
vis[SON] = true;
dis[S][SON] = dis[S][tp] + 1;
q.push(SON);
}
}
}
int main(){
N = read(), M = read(), K = read();
for(int i = 1; i <= M; ++i){
int f = read(), t = read();
head[f] = new Edge{head[f], t + N};
head[t + N] = new Edge{head[t + N], f};
head[t] = new Edge{head[t], f + N};
head[f + N] = new Edge{head[f + N], t};
}
for(int i = 1; i <= N; ++i)bfs(i);
for(int i = 1; i <= K; ++i){
int f = read(), t = read(), d = read();
int diss = dis[f][(d & 1) ? t + N : t];
printf("%s\n", diss && d >= diss ? "TAK" : "NIE");
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3563 [POI2013]POL-Polarization
题面
给定一棵有 $ n $ 个节点的树,要求将树上所有边变成有向边,求本质不同连通点对的最小和最大对数。
定义本质不同连通点对为对于点 $ a, b $,满足 $ a $ 能到达 $ b $,或 $ b $ 能到达 $ a $。
$ n \le 2.5 \times 10^5 $。
Examples
Input_1
4 1 2 1 3 1 4
Output_1
3 5
Solution
该说不说这道题的数据有点水,可以微调块长然后用一个不正确的贪心水过去。。。
首先对于第一个问题应该比较简单,如果说的专业一点就是,树是一个二部图,将其分解为左右部图后,把部图间的无向边全部改为左部图向右部图的有向边(反之亦然),则最小值一定为 $ n - 1 $。
或者通俗地说,把 $ i $ 到 $ i + 1 $ 层之间的边和 $ i + 1 $ 到 $ i + 2 $ 层之间的边反向连结,最终一定有 $ n - 1 $ 对连通点对。
对于第二个问题需要引入几个我不会证明很神奇的 Lemma:
Lemma 1:对于一个使连通点对数量最多的图,其中一定至少有一个点满足以其为根,所有子树要么是外向的要么是内向的,也就是说要么全部指向根方向,要么全部背向根方向。
Lemma 2:对于一个使连通点对数量最多的图,Lemma 1 的这个点一定在树的任意一个重心上。
证明:The proof is left to the reader. (不会证)
于是我们便可以发现,这道题的思路就是找到树的重心,然后以重心为根搜一下其每个子树的大小,记录下来之后枚举哪些子树是外向的,哪些是内向的,才会使最终答案最优。
如果是菊花图的话子树个数最多是 $ n $ 级别的,那么嗯枚举的话大概是 $ O(2^n) $ 显然不可以通过,考虑优化。
首先我们接着刚才的思路往下想此时我们根已经确定了,假设我们有这样一个图:
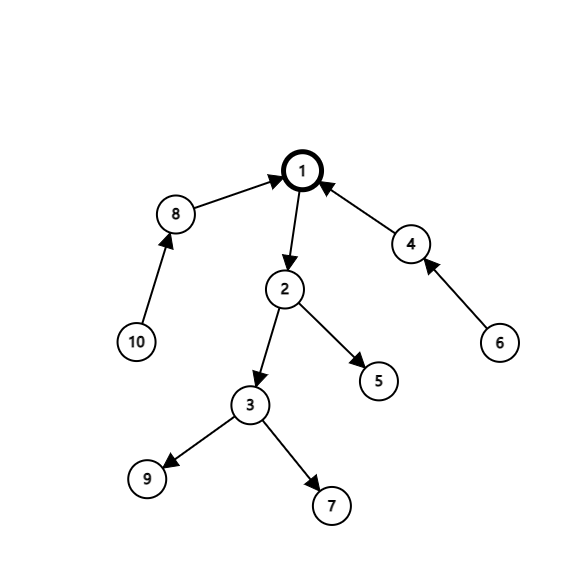
我们考虑除了根节点外的每一个节点,不难发现我们现在若仅考虑对每一个节点和该节点的所有子节点最高到达该节点的父亲的连通对,那么如果我们令节点 $ i $ 为根的子树大小为 $ siz_i $,那么显然上述的所有联通对的个数为 $ \sum siz_i $。
在这之后我们便不难发现只剩下如 $ (10, 3) $,即 $ 10 \rightarrow 8 \rightarrow 1 \rightarrow 2 \rightarrow 3 $,这种通过根节点的路径形成的连通对没有考虑,于是联想到我们之前的 Lemma,如果我们设所有内向的子树大小之和为 $ k_1 $,所有外向的子树大小之和为 $ k_2 $,且显然有 $ k_1 + k_2 = n - 1 $,不难想到这种情况中的连通对数量即为 $ k_1 \times k_2 $。
于是显然有 $ ans = \sum siz_i + k_1 \times k_2 $,当根确定之后前者一定是固定的,那么我们就只需要考虑什么时候后者最大即可。
我们将所有子树大小抽象成一个序列,那么我们的目标就是要将这个序列分成两部分,使两部分分别求和后乘积最大。两个数和固定,要让积最大,这玩意应该很显然就是要让两个数相等吧,放到这道题上就是让两部分的求和后的差值最小,这东西不觉得非常像搭建双塔吗。。。关于一个人类智慧的DP - Vijos 1037 搭建双塔
不过我们仔细观察一下后发现实际上并不一样,本题里我们需要将所有的数都用上,且搭建双塔的时间复杂度放在这题上就很离谱了。
首先这里提供一个奇怪的贪心,据说是 2015 集训队论文里的(虽然我没找到)(而且是错误的),大概就是维护一个大根堆,然后每次取堆顶的两个值,计算它们差的绝对值然后再插入堆里,当堆中剩余一个元素的时候这个元素就是差值的最小值,看起来似乎很奇怪,细想一下似乎很正确,但是这是错误的(如果不是我想错了的话)。
这个贪心大概的思路就是每次找最大的两个分别放在两侧,会有一个差值,然后我们可以将这个差值也认为是一个新的数,显然差值也可以和普通的数一样放置,比如说两对差值为 $ 1 $ 的块全部拼在一起最终的差值也就是 $ 0 $ 了,这里如果你做过搭建双塔的话大概也就能看出来错误在哪里了,显然我们贪心地取两个最大的放在两侧并不一定是最优的,比如这样一个序列:$ 3, 3, 3, 3, 3, 3, 3, 3, 8, 8, 8 $,显然 $ 8 $ 放在一起,$ 3 $ 放在一起,最终差值为 $ 0 $,但是按照这个贪心则会优先把两个 $ 8 $ 放在一起抵消,导致最后剩下的差值为 $ 2 $。
但是这个东西是可以过的,可以发现如果进行根号分治,但是不按照 $ \sqrt{n} $ 分治而是固定按照 $ 1000 $ 的话,那么刚好可以把这个贪心不正确的数据点在时间复杂度允许的情况下用正常的 DP + bitset 求解,最后无论是 Luogu 的十个数据点还是原题的六十多个数据点都是可以 Accept 的,就算按照标准的根号分支也可以过接近 $ 90% $ 的点,不过不能怪数据弱,确实这个是很难卡的。
Code:
const int B = 1000;//int(sqrt(N));
if(tot >= B){
std::priority_queue < int, vector < int >, less < int > > vals;
for(auto i : subt)vals.push(i);
while(vals.size() != 1){
int x = vals.top(); vals.pop();
int y = vals.top(); vals.pop();
vals.push(abs(x - y));
}
int diff = vals.top();
int vx = (N - 1 - diff) / 2;
int vy = vx + diff;
ans += (ll)vx * vy;
}else{
dp[0] = true;
for(auto i : subt)dp |= dp << i;
for(int i = N / 2 + 1; i >= 0 ; --i)if(dp[i]){ans += (ll)i * (N - i - 1); break;}
}
考虑正解,开一个大小为 $ n $ 的 bool 类型数组,表示 $ k_1 $ 是否能为 $ i $(或表示 $ k_2 $ 同理)显然是一个 $ O(n^2) $ 的 DP,转移之后从 $ \dfrac{n}{2} $ 开始跑,跑到的第一个可行解一定为最优解,使两者差最小,但是这个复杂度显然不正确。考虑子树的个数,如果小于 $ \sqrt{n} $ 那么显然这个复杂度实际上是 $ O(n\sqrt{n}) $ 的,如果大于 $ \sqrt{n} $,则子树最大值一定是小于 $ \sqrt{n} $ 的,也就是一定有相同大小的子树,且随着子树个数增多,最大值会逐渐变小,导致重复的个数继续增大,此时我们可以以多重背包的思想取考虑,将多个相同大小的子树拆成 $ 2^0, 2^1, 2^1, \cdots $,变成多个背包,令大小为 $ i $ 的子树有 $ cnt_i $ 个,最后的复杂度大概是一个 $ O(n\sum \log cnt_i) $,这个东西大概使介于 $ O(n\log n) $ 和 $ O(n\sqrt{n}) $ 之间的,具体证明我也不知道应该怎么证,感性理解一下吧。
然后发现复杂度依然不正确,考虑把这个数组压成一个 bitset,这样在进行或运算的时候还可以大幅降低速度,最终是 $ O(\dfrac{n\sqrt{n}}{\omega}) $,此处的 $ \omega $ 一般为 $ 32 $,显然可以通过。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[510000];
ROPNEW(ed);
Edge* head[260000];
int N;
int siz[260000], msiz[260000], rt(0);
void dfs(int p, int fa = -1){
msiz[p] = 0;
siz[p] = 1;
for(auto i = head[p]; i; i = i->nxt){
if(SON == fa)continue;
dfs(SON, p);
siz[p] += siz[SON];
msiz[p] = max(msiz[p], siz[SON]);
}
msiz[p] = max(msiz[p], N - siz[p]);
if(!rt || msiz[p] < msiz[rt])rt = p;
}
int cnt[260000];
int tot(0);
ll ans(0);
bitset < 260000 > dp;
int main(){
N = read();
for(int i = 1; i <= N - 1; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
}
dfs(1);
dfs(rt);
for(int i = 1; i <= N; ++i)if(i != rt)ans += siz[i];
for(auto i = head[rt]; i; i = i->nxt)cnt[siz[SON]]++;
for(int i = 1; i <= N / 2; ++i)while(cnt[i] > 2)cnt[i] -= 2, cnt[i * 2]++;
dp[0] = true;
for(int i = 1; i <= N; ++i)while(cnt[i]--)dp |= dp << i;
for(int i = N / 2; i >= 0 ; --i)if(dp[i]){ans += (ll)i * (N - i - 1); break;}
printf("%d %lld\n", N - 1, ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3551 [POI2013]USU-Take-out
题面
给定 $ n $ 块黑白砖,其中白色数量是黑色的 $ k $ 倍,你要消除这些砖块,求出一个消除序列,满足以下条件:
每次消除 $ k + 1 $ 块砖,其中 $ k $ 块白色,$ 1 $ 块黑色,且这 $ k + 1 $ 块砖从开始到结束中间不能路过已经消除的砖块。
$ 2 \le n \le 10^6, 1 \le k \le n - 1 $。
其中 $ c $ 表示黑色砖块,$ b $ 表示白色砖块,保证数据有解。
输入格式
$ n \quad k $
Describe the brick sequence.
Examples
Input_1
12 2 ccbcbbbbbbcb
Output_1
1 8 12 2 6 7 3 4 5 9 10 11
Solution
正难则反(怎么又是正难则反)。
我估计你们都能简单想出来个大致的思路,但是吧这玩意需要个关键的性质:
对于一个有解的序列,只要其满足白色块是黑色的 $ k $ 倍,就一定仍然有解。
但是这个性质并没有找到任何的证明。。。只能感性理解一下这个似乎是正确的。。。吧?
所以我们逆向去思考,我们最后删除的一定是一段连续的 $ k $ 个白块和 $ 1 $ 个黑块,删除后剩下的序列一定也可以按照这个规则继续删下去,并且其中具体删去哪段序列并不会影响有解,这个通过前面的那个性质很容易就能得到证明。
考虑维护个栈,并且维护一个类似滑动窗口的东西,也就是维护栈中最后 $ k + 1 $ 个元素有多少个黑色块,可以用一个类似动态前缀和的东西,当最后 $ k + 1 $ 刚好有 $ 1 $ 个黑色块时,显然这一段时合法序列,将其删去并记录即可,最后逆序输出所有解即可 Accept。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
bool readc(void){
char c = getchar();
while(c != 'c' && c != 'b')c = getchar();
return c == 'c' ? true : false;
}
int N, K;
stack < int > seq;
int sum[1010000];
int cnt(0);
std::priority_queue < int, vector < int >, greater < int > > ans[1010000];
int main(){
N = read(), K = read();
for(int i = 1; i <= N; ++i){
bool f = readc();
seq.push(i);
sum[seq.size()] = sum[seq.size() - 1] + f;
if((int)seq.size() >= K + 1 && sum[seq.size()] - sum[seq.size() - K - 1] == 1){
++cnt;
for(int j = 1; j <= K + 1; ++j)ans[cnt].push(seq.top()), seq.pop();
}
}
for(int i = cnt; i >= 1; --i){
while(!ans[i].empty()){
int v = ans[i].top(); ans[i].pop();
printf("%d ", v);
}printf("\n");
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3553 [POI2013]INS-Inspector
题面
给你一个公司,公司里有 $ n $ 个员工,在某一天里,每一位员工只会工作连续的一段时间。现给定这天 $ m $ 条记录,每条记录为 $ t_i, a_i, x_i $,代表 $ t_i $ 的时间由 $ a_i $ 记录,除了 $ a_i $ 之外还有 $ x_i $ 名员工正在工作。求最大的前 $ k $ 条记录之间互不矛盾。
多组数据,数据组数为 $ T $。
$ 1 \le T \le 50, 1 \le n, m \le 10^5, 1 \le t_i \le m, 1 \le a_i, x_i \le n $。
输入格式
$ T $
$ n, m $
$ t_i, a_i, x_i $
$ \cdots $
Examples
Input_1
2 3 5 1 1 1 1 2 1 2 3 1 4 1 1 4 2 1 3 3 3 3 0 2 2 0 1 1 0
Output_1
4 3
Solution
题目本身并没有什么高深的算法或者奇怪的思路,嗯做即可。
二分答案应该很显然吧???这样可以把求解改为验证正确性。
不难想到我们可以把每个人抽象成一个线段,那么每个人都有一个必须要覆盖的区间,也就是会有一段时间段里某个人必须一直工作,并且他们覆盖的区间在合法的情况下是可以向左右无限延伸的,而对于没有任何的限制的人我们可以认为他们是自由的,可以随意延申,区间没有被确定。
我们先将这个处理出来,然后整体跑一遍,过程中可以考虑维护以下几个状态:
$ cur $:当前必须要选择多少人工作。
$ fre $:还有多少人是自由的。
$ extl $:有多少人还没到其必须工作的区间,但为了尽可能有解所以必须向左延申。
$ extr $:有多少人已经到或者越过其必须工作的区间,并且可以向右继续延申。
然后还需要注意特判一下一些无解的情况,比如有两个人的描述冲突,自由的人变为负数,所有能用的人加一起都无法满足必须要选择的人数等,跑一圈即可,注意每次判断时的初始化。
时间复杂度大概是 $ O((n + m) \log m) $,显然能过。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
tm/tim => time
lt/lft => left
bg => begin
ed => end
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MAXNM 110000
#define CLEAR(arr) memset(arr, 0, sizeof(arr))
template<typename T = int>
inline T read(void);
int N, M;
tuple < int, int, int > in[MAXNM];
struct Worker{int l, r;}wk[MAXNM];
int bg[MAXNM], ed[MAXNM];
int note[MAXNM];
void clear(void){
CLEAR(wk);
CLEAR(note);
CLEAR(bg), CLEAR(ed);
}
bool check(int lim){
clear();
for(int i = 1; i <= lim; ++i){
int tm, n, lt;
tie(tm, n, lt) = in[i];
if(note[tm] && note[tm] != lt)return false;
note[tm] = lt,
wk[n].l = min(wk[n].l ? wk[n].l : INT_MAX, tm),
wk[n].r = max(wk[n].r, tm);
}
for(int i = 1; i <= N; ++i)if(wk[i].r)++bg[wk[i].l], ++ed[wk[i].r];
int cur(0), fre(N), extl(0), extr(0);
for(int i = 1; i <= M; ++i){
if(!note[i])continue;
cur += bg[i];
if(cur > note[i])return false;
while(bg[i]--)extl ? --extl : --fre;
while(cur + extl + extr < note[i])--fre, ++extl;
if(fre < 0)return false;
while(cur + extl + extr > note[i])extr ? --extr : --extl;
extr += ed[i], cur -= ed[i];
}
return true;
}
int main(){
int T = read();
while(T--){
// in.clear(), in.shrink_to_fit();
N = read(), M = read();
for(int i = 1; i <= M; ++i){
int tm = read(), num = read(), lft = read(); ++lft;
in[i] = {tm, num, lft};
}
int l = 1, r = M;
int ans(-1);
while(l <= r){
int mid = (l + r) >> 1;
check(mid) ? l = mid + 1, ans = mid : r = mid - 1;
}
printf("%d\n", ans);
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3557 [POI2013]GRA-Tower Defense Game
题面
给定一张 $ n $ 个点 $ m $ 条边的无向图,一直用 $ k $ 个攻击距离为 $ 1 $(也就是可以攻击到所有相邻节点)的防御塔可以覆盖攻击到整个地图,请构造一个方案,使得用不超过 $ k $ 个攻击距离为 $ 2 $ 的塔攻击到整个地图,保证有解
输入格式
$ n, m, k $
Describe the graph.
Examples
Input_1
9 8 3 1 2 2 3 3 4 1 4 3 5 4 6 7 8 8 9
Output_1
3 1 5 7
Solution
这题真的是近期一段时间内做过最舒服的题了。
什么普及减。
看起来很高端的一道构造题,我第一眼看到这道题也有点迷,用 $ k $ 个距离为 $ 1 $ 的塔,用距离为 $ 2 $ 的塔的时候还是 $ k $ 个???
我还以为是翻译的问题,可能是 SPJ 最多 $ k $ 个,满分有一个更小的要求呢。。。结果最后找了半天才发现这玩意真就小于等于 $ k $ 个就 Accept。
于是我们简单动一丢丢脑子想一下就会发现,既然摆 $ k $ 个有解,那么我们就直接遍历所有节点,如果没有被覆盖的就直接放一座防御塔,然后搜一下距离小于等于 $ 2 $ 的标记一下,然后再找下一个没有被覆盖的直接放。
乍一看这个似乎很假,感觉一定不是很优,但是我们细想一下,这个东西实际上是可以证明的。
既然我们摆放 $ k $ 个攻击距离为 $ 1 $ 的防御塔是可以覆盖全图的,那么对于原来的图中的点一定满足:要么被放置了一个防御塔,要么距离最近的防御塔的距离为 $ 1 $。于是考虑我们放的攻击距离为 $ 2 $ 的塔,如果放在原来放置小防御塔的地方,一定仍然可以覆盖原来的小防御塔可以覆盖的点。如果放置在原来距离为 $ 1 $ 的点,到达原来的防御塔后剩余的可攻击距离一定仍然还有 $ 1 $,那么依然一定不会比原来更劣,所以正确性可以证明,几分钟就能过,名副其实的水题。
时间复杂度:这个应该算是 $ O(n) $ 吧。。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[2100000];
ROPNEW(ed);
Edge* head[510000];
int N, M, K;
bool atk[510000];
int cnt(0);
void Attack(int p, int dis = 0){
atk[p] = true;
if(dis >= 2)return;
for(auto i = head[p]; i; i = i->nxt)Attack(SON, dis + 1);
}
int main(){
N = read(), M = read(), K = read();
for(int i = 1; i <= M; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
}
vector < int > ans;
for(int i = 1; i <= N; ++i)if(!atk[i])ans.push_back(i), Attack(i);
printf("%d\n", (int)ans.size());
for(auto i : ans)printf("%d ", i);
printf("\n");
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3554 [POI2013]LUK-Triumphal arch
题面
给定一棵 $ n $ 个节点的树,初始的时候 $ 1 $ 节点被染黑,其余节点均为白色,A B 两人轮流操作,每一轮中,A 先选择 $ k $ 个点染黑,然后 B 走到一个相邻的节点,若 B 走到了白色点上则 B 获胜,反之当整棵树都被染黑时,A 获胜,求能够使 A 一定获胜的最小的 $ k $。
$ n \le 3 \times 10^5 $。
Examples
Input_1
7 1 2 1 3 2 5 2 6 7 2 4 1
Output_1
3
Solution
这道题拿到手之后就口糊了一个感觉还挺正确的贪心算法,后来看了一下跟正解还是比较相似的,二分答案应该很显然,首先 dfs 预处以 $ 1 $ 为根每个结点的深度和父亲,然后每一轮先判断能不能把相邻子节点全部染色,然后写个值为 tuple < int, int, int > 的 std::priority_queue,手写一个比较函数,处理一下每个点剩余的没有被染色的子节点数和深度,优先染深度较浅的,深度相同的情况下优先染子节点数更多的点的子节点,然后再把它丢回去找子节点数最多的继续去染他的子节点,直到多出来的染色次数用完。
没怎么分析复杂度,加了点剪枝,感觉复杂度会很奇怪,最终也验证了我的猜想,正确性似乎没什么问题,但是时间上直接爆炸,$ 90% $ TLE,无奈开始翻题解,发现大致的思想是正确的,只是正解用的是树形 DP。
大概的思路也还是先 dfs 以下求子节点数(这一步可以省略,仅为了剪枝而存在)。
然后依然是二分答案,显然这步是可以剪枝的,下界就是根节点的子节点数,上界就是所有点中最大的子节点数。
思考这题的一个很显然的思路,如果我们目光短浅一点只考虑当前点的话,很显然一个正确的贪心策略就是优先把当前所在点的所有子节点都染成黑色,否则 B 就直接获胜了。然后剩余染色次数才可以给子节点,于是我们可以考虑记录每个节点需要多少“帮助”才能达到要求,令其为 $ dp(i) $,显然我们可以从叶子节点往根推一遍,方程很显然,令节点的子节点数为 $ s(i) \(,\) j $ 为 $ i $ 的子节点,$ dp(i) = s(i) - k + \sum \max(dp(j), 0) $。
复杂度是 $ O(n \log v) $,如果不剪枝的话就是 $ O(n \log n) $,显然可以通过。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[610000];
ROPNEW(ed);
Edge* head[310000];
int N;
int cson[310000];
int dp[310000];
void dfs(int p = 1, int fa = 0){
for(auto i = head[p]; i; i = i->nxt)if(SON != fa)++cson[p], dfs(SON, p);
}
void MakeDP(int k, int p = 1, int fa = 0){
dp[p] = cson[p] - k;
for(auto i = head[p]; i; i = i->nxt)
if(SON != fa){
MakeDP(k, SON, p);
dp[p] += max(0, dp[SON]);
}
}
bool check(int k){
MakeDP(k);
return dp[1] <= 0;
}
int main(){
N = read();
for(int i = 1; i <= N - 1; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
}
dfs();
int l = cson[1], r = N - 1, ans = -1;
while(l <= r){
int mid = (l + r) >> 1;
check(mid) ? ans = mid, r = mid - 1 : l = mid + 1;
}printf("%d\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3547 [POI2013]CEN-Price List
题面
给定一个边权均为 $ a $ 的无向图,对于每个 $ u, v $,若两者之间最短路为 $ 2a $,则在两点之间再建立一条长度为 $ b $ 的边,给定一个点 $ k $,求在这之后图上每个点到 $ k $ 的最短路,无重边无自环。
$ 2 \le n \le 10^5, 1 \le m \le 10^5, 1 \le k \le n, 1 \le a, b, \le 10^3 $。
输入格式
$ n, m, k, a, b $
Describe the graph.
Examples
Input_1
5 5 1 3 2 1 2 2 3 3 4 4 5 3 1
Output_1
0 3 3 2 5
Solution
这题我感觉不太像黑的啊,紫色比较合适吧。。。
显然我们考虑对于任意两个点 $ u, w $,且这两个点之间的存在最短路径 $ u \rightarrow v \rightarrow w $,那么显然如果 $ 2a \le b $,那么最短路一定是只选择走长度为 $ a $ 的边更优,如果有 $ 2a \gt b $,那么显然我们要尽可能地选择更多的长度为 $ b $ 的路径。而长度为 $ b $ 的路径每次可以认为是走了两段 $ a $ 路径,如果宽搜的话可能最终会剩余一个 $ a $ 路径,但是如果存在 $ b \ll a $,那么我们绕路多走几次 $ b $ 从而避免走 $ a $ 可能会更优。于是此时我们,令仅走 $ a $ 边的最短距离为 $ dis $,仅走 $ b $ 边的最短距离为 $ dis' $,便可以发现一共实际上只有三种可能的情况:
- 走了 $ dis $ 次 $ a $ 路径。
- 走了 $ \lfloor \dfrac{dis}{2} \rfloor $ 次 $ b $ 路径和 $ dis \bmod{2} $ 次 $ a $ 路径。
- 走了 $ dis' $ 次 $ b $ 路径。
显然前两种都可以通过宽搜 $ O(n) $ 实现,最终的式子大概是 $ \min(dis \times a, \lfloor \dfrac{dis}{2} \rfloor \times b + (dis \bmod{2}) \times a) $。对于第三种情况,容易想到一个简单的暴力方式,即对于每一个点枚举它的子节点,再枚举其子节点的子节点,如果构成环那么两者之间没有 $ b $ 边,否则可以进行更新,这个复杂度显然是 $ O(m^2) $ 的,无法通过。观察发现此题和三元环计数很像,于是我们考虑类似的剪枝,当我们枚举 $ u \rightarrow v \rightarrow w $ 的时候,对于 $ v \rightarrow w $ 或者 $ w \rightarrow v $ 显然在此之后的作为”第二条边“的更新是没有用的,可以以类似 Dijkstra 的思想考虑,当我们第一次更新 $ w $ 的时候一定是最优的一次,此时的 $ w $ 已经确定了,当我们再次使用新的 $ u' $ 去更新 $ w $ 的时候,一定有 $ dis(u') \ge dis(u) $,所以是没有必要的。但是这里需要注意只是在更新第二条边的时候可以不用重复考虑同一条边,对于第一条边仍需考虑,因为你在枚举 $ u \rightarrow v $ 的时候只是把 $ v $ 当作一个”跳板“,并没有去更新 $ v $,所以我们需要维护两个边集,枚举第一条边使用前者,枚举第二条边使用后者并同时删边,最终复杂度为 $ O(m \sqrt{m}) $。
关于复杂度的证明和三元环计数差不多,大概就是从度数和 $ \sqrt{m} $ 之间的大小关系入手,分别讨论,这里同时提供 POI 官方的一个非常巧妙的证明方法:
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
vector < int > vert[110000], dvert[110000];
int N, M;
int K, a, b;
int dis[110000];
bool vis[110000];
int tag[110000];
int ans[110000];
int main(){
N = read(), M = read(), K = read(), a = read(), b = read();
for(int i = 1; i <= M; ++i){
int s = read(), t = read();
vert[s].push_back(t), vert[t].push_back(s);
dvert[s].push_back(t), dvert[t].push_back(s);
}
queue < int > vrt;
vrt.push(K); vis[K] = true;
while(!vrt.empty()){
int p = vrt.front(); vrt.pop();
for(auto i : vert[p])
if(!vis[i])dis[i] = dis[p] + 1, vis[i] = true, vrt.push(i);
}
for(int i = 1; i <= N; ++i)ans[i] = min(dis[i] * a, (dis[i] / 2 * b + (dis[i] & 1) * a));
memset(dis, -1, sizeof(dis));
vrt.push(K); dis[K] = 0;
while(!vrt.empty()){
int p = vrt.front(); vrt.pop();
for(auto i : vert[p])tag[i] = p;
for(auto i : vert[p]){
auto it = dvert[i].begin();
while(it != dvert[i].end()){
if(tag[*it] == p || ~dis[*it])++it;
else vrt.push(*it), dis[*it] = dis[p] + 1, it = dvert[i].erase(it);
}
}
}
for(int i = 1; i <= N; ++i)if(~dis[i])ans[i] = min(ans[i], dis[i] * b);
for(int i = 1; i <= N; ++i)printf("%d\n", ans[i]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3562 [POI2013] LAS-Laser
题面
给定平面上的 $ n $ 条线段(用点 $ (x_1, y_1), (x_2, y_2) $ 表示),你可以从原点引出最多 $ k $ 条射线,使其穿过尽可能多的线段,且每条线段最多被穿过 $ 1 $ 次,求最多可以穿过多少条线段。
$ 1 \le n \le 5 \times 10^5, 1 \le k \le 100, 1 \le x_1, y_1, x_2, y_2 \le 10^5 $。
输入格式
$ n, k $
$ x_1, y_1, x_2, y_2 $
$ \cdots $ (n lines in total)
Examples
Input_1
3 6 1 2 2 4 3 1 5 1 3 2 2 3 3 3 3 4 2 2 2 2 6 1 3 5
Output_1
5
Solution
首先本题有一个比较显而易见的贪心,即最优的情况下每条射线至少穿过一条线段的端点,感性理解一下,如果不穿过端点那么移动到端点一定是不劣的。
我们可以考虑一个类似极角排序的思想,把每一个点当成一个向量的坐标表示,按照角度进行排序离散化并尝试寻找性质:
可以看下图:
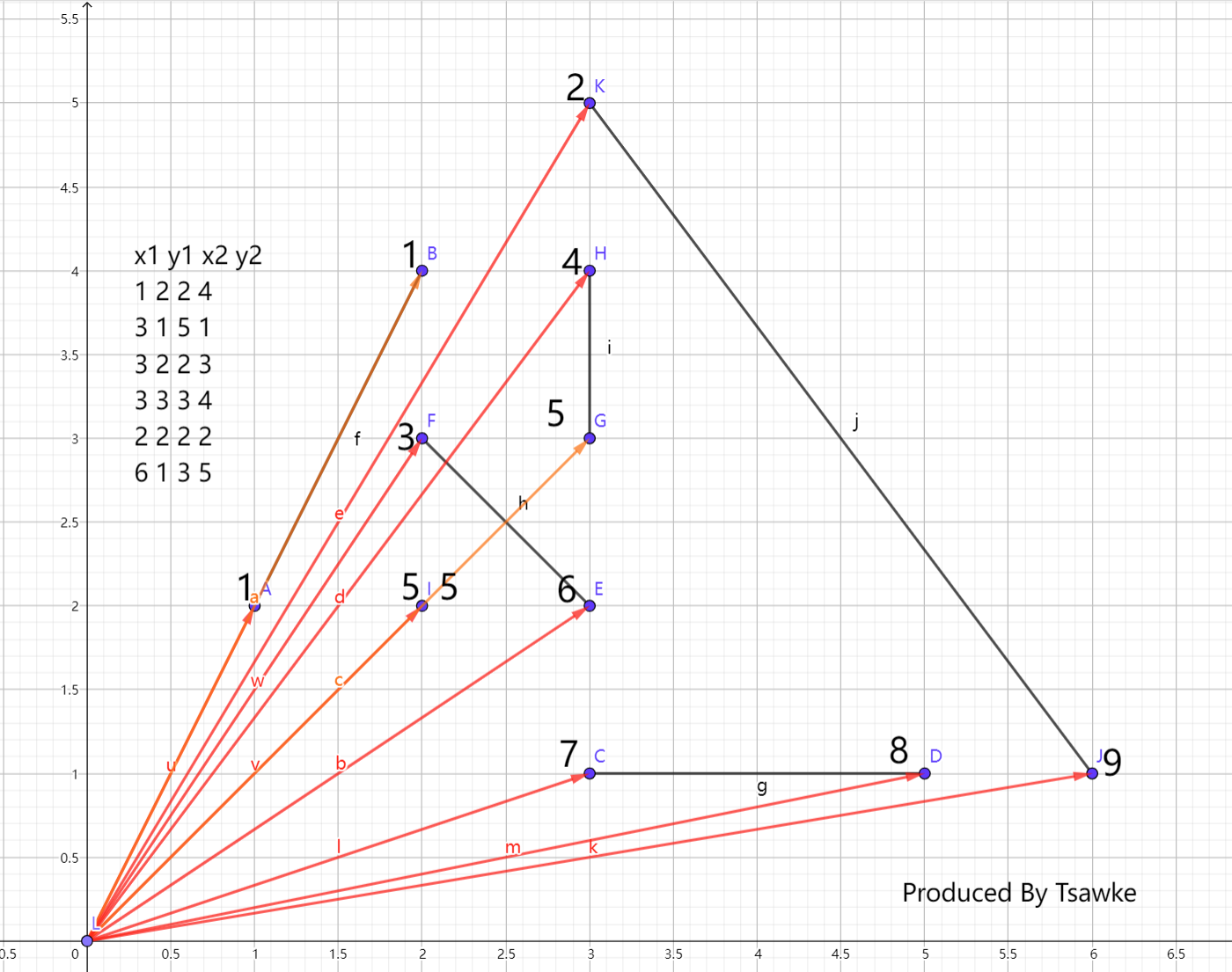
排序离散化后,每个点旁边的数字即为其离散化后的坐标,于是我们发现,每一条线段都变成了一个区间:
$ \left[ 1, 1 \right], \left[ 7, 8 \right], \left[ 3, 6 \right], \left[ 4, 5 \right], \left[ 5, 5 \right], \left[ 2, 9 \right] $。
同时注意,离散化后的每一个点都是至少一个区间的端点!
而我们从原点引出的每一条射线,也可以抽象成一个向量的坐标,或者换句话说,是这些区间中的一个点。
于是此时我们便可以发现问题变成了在给定区间中选择一些点,使这些点涉及的区间尽可能多,且每个区间中最多只有一个点。
对于这个问题应该是一个显然的 DP,我们考虑设 $ dp(i, j) $ 表示在前 $ i $ 个点(等同于区间端点)中选择 $ j $ 个点最多可以涉及多少个区间。
考虑转移,显然可以通过 $ dp(i - 1, j) $ 转移,同时我们也可以考虑如果选择第 $ i $ 个点,那么应该从什么区间转移而来?
显然选择第 $ i $ 个点后,其所涉及的所有区间都不能有其它的点,所以我们应该记录 $ i $ 所涉及的所有的区间中最左的端点,记其为 $ lft(i) $,同时记点 $ i $ 涉及的区间的数量为 $ cnt(i) $,那么也就是从 $ dp(lft(i) - 1, j - 1) + cnt(i) $ 转移而来。
于是我们的方程便为 $ dp(i, j) = \max(dp(i - 1, j), dp(lft(i) - 1, j - 1) + cnt(i)) $。
通过差分预处理一下 $ lft $ 和 $ cnt $ 即可。
然后注意观察到 $ i $ 的值域是 $ 5 \times 10^5 \(,\) j $ 的值域是 $ 10^2 $,所以空间占用为 $ \dfrac{5 \times 10^5 \times 10^2 \times 4}{1024^2} \gt 128 $,空间会炸,发现 $ j $ 只会从 $ j $ 或 $ j - 1 $ 转移而来,所以可以以类似写背包时候的思想把 $ j $ 的维度去掉,将不同版本考虑好即可。
时间复杂度是 $ O(n(\log n + k)) $ 的,显然可以通过。
Tips:对于具体的离散化实现,可以通过向量的外积,大于零则前者在后者的顺时针方向,反之亦然,可以考虑写个结构体重载小于号和等于号,或者在 sort 和 unique 和 lower_bound 的时候写个 lambda 函数也行,亦或自己纯手搓一个离散化也可以实现,具体可以看代码。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
segl => line segment
lft => left
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
struct Point{
int x, y;
friend ll operator * (const Point &a, const Point &b){
return (ll)a.x * b.y - (ll)a.y * b.x;
}
friend bool operator < (const Point &a, const Point &b){
return a * b < 0;
}
friend bool operator == (const Point &a, const Point &b){
return a * b == 0;
}
};
int K, N;
pair < Point, Point > segl[510000];
pair < int, int > seg[510000];
vector < Point > arr;
int cnt[1100000];
int lft[1100000];
int dp[1100000];
int main(){
K = read(), N = read();
for(int i = 1; i <= N; ++i){
int x1 = read(), y1 = read(), x2 = read(), y2 = read();
segl[i] = {Point{x1, y1}, Point{x2, y2}};
arr.push_back(Point{x1, y1}), arr.push_back(Point{x2, y2});
}
sort(arr.begin(), arr.end(), [](const Point &a, const Point &b)->bool{return a * b < 0;});
auto endpos = unique(arr.begin(), arr.end());
int siz = distance(arr.begin(), endpos);
for(int i = 1; i <= N; ++i){
seg[i].first = distance(arr.begin(), lower_bound(arr.begin(), endpos, segl[i].first) + 1);
seg[i].second = distance(arr.begin(), lower_bound(arr.begin(), endpos, segl[i].second) + 1);
if(seg[i].first > seg[i].second)swap(seg[i].first, seg[i].second);
}
for(int i = 1; i <= siz; ++i)lft[i] = siz;
for(int i = 1; i <= N; ++i){
++cnt[seg[i].first], --cnt[seg[i].second + 1];
lft[seg[i].second] = min(lft[seg[i].second], seg[i].first);
}
for(int i = 1; i <= siz; ++i)cnt[i] += cnt[i - 1];
for(int i = siz - 1; i >= 1; --i)lft[i] = min(lft[i], lft[i + 1]);
for(int j = 1; j <= K; ++j){
for(int i = siz; i >= 1; --i)dp[i] = max(dp[i], dp[lft[i] - 1] + cnt[i]);
for(int i = 1; i <= siz; ++i)dp[i] = max(dp[i], dp[i - 1]);
}
printf("%d\n", dp[siz]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3548 [POI2013] GOB-Tapestries
题面 & Solution
一道 Luogu 上通过为 $ 1 $,网上中文英文题解都几乎没有的阴间计算几何。
本来准备 skip,然后在某位学长的 Blog 里找到了个题解,于是想尝试一下,写了一半,然后知道了计算几何在 NOI 系列比赛里基本不考,然后。。。
咕咕咕。
关于某个唯一找到的不是波兰文的题解 戳此进入。
Code(incomplete)
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template<typename T = int>
inline T read(void);
bool readflag(void);
struct Point{
ld x, y;
friend Point operator + (const Point &a, const Point &b){
return Point{a.x + b.x, a.y + b.y};
}
friend Point operator - (const Point &a, const Point &b){
return Point{a.x - b.x, a.y - b.y};
}
friend Point operator * (const ld &k, const Point &a){
return Point{k * a.x, k * a.y};
}
};
struct Vec{
ld x, y;
friend ld operator * (const Vec &a, const Vec &b){
return (ld)a.x * b.y - (ld)a.y * b.x;
}
friend bool operator < (const Vec &a, const Vec &b){
return a * b < 0;//TODO eps
}
friend bool operator > (const Vec &a, const Vec &b){
return a * b > 0;
}
friend bool operator == (const Vec &a, const Vec &b){
return a * b == 0;
}
};
Vec MakeVec(Point a, Point b){return Vec{b.x - a.x, b.y - a.y};}
Vec Point2Vec(Point p){return Vec{p.x, p.y};}
Point Vec2Point(Vec v){return Point{v.x, v.y};}
struct Line{
Point P;
Vec V;
};
Line MakeLine(Point a, Point b){return Line{Point{a.x, a.y}, MakeVec(a, b)};}
struct Segl{
Point a, b;
};
int N;
Point p[1100];
int JudgePointPos(Point a, Line l){// 1 - left; -1 - right; 0 - on
auto ret = l.V * MakeVec(l.P, a);
return ret > 0 ? 1 : (ret < 0 ? -1 : 0);
}
int JudgeSeglPos(Segl sl, Line l){// 1 - left; -1 - right; 0 - cross
int a = JudgePointPos(sl.a, l), b = JudgePointPos(sl.b, l);
return (a == 1 && b == -1) || (a == -1 && b == 1)
? 0
: (a == 1 || b == 1)
? 1
: -1;
}
Point GetInter(Line l1, Line l2){//Intersection
ld k = (ld)(Point2Vec(l2.P - l1.P) * l2.V) / (ld)(l1.V * l2.V);
return l1.P + k * Vec2Point(l1.V);
}
bool check(void){
}
int main(){
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
bool readflag(void){
char c = getchar();
while(c != 'C' && c != 'S')c = getchar();
return c == 'S' ? true : false;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P3559 [POI2013] LAB-Maze
题面 & Solution
一道似乎比上一题更离谱的计算几何,依然完全没有任何题解,只有波兰文的。
咕咕咕。
LG-P3549 [POI2013]MUL-Multidrink
题面
一道论文题。
给定一棵有 $ n $ 个节点的树,令起点为 $ 1 $,终点为 $ n $,每步可以走的距离为 $ 1 $ 或 $ 2 $,要求不重复地遍历 $ n $ 个节点。
如果无解输出 BARK,否则输出 $ n $ 行,表示遍历的路径,存在 SPJ。
$ 1 \le n \le 5 \times 10^5 $。
输入格式
$ n $
Describe the tree($ n - 1 $ lines in total).
Examples
Input_1
12 1 7 7 8 7 11 7 2 2 4 4 10 2 5 5 9 2 6 3 6 3 12
Output_1
1 11 8 7 4 10 2 9 5 6 3 12
图例
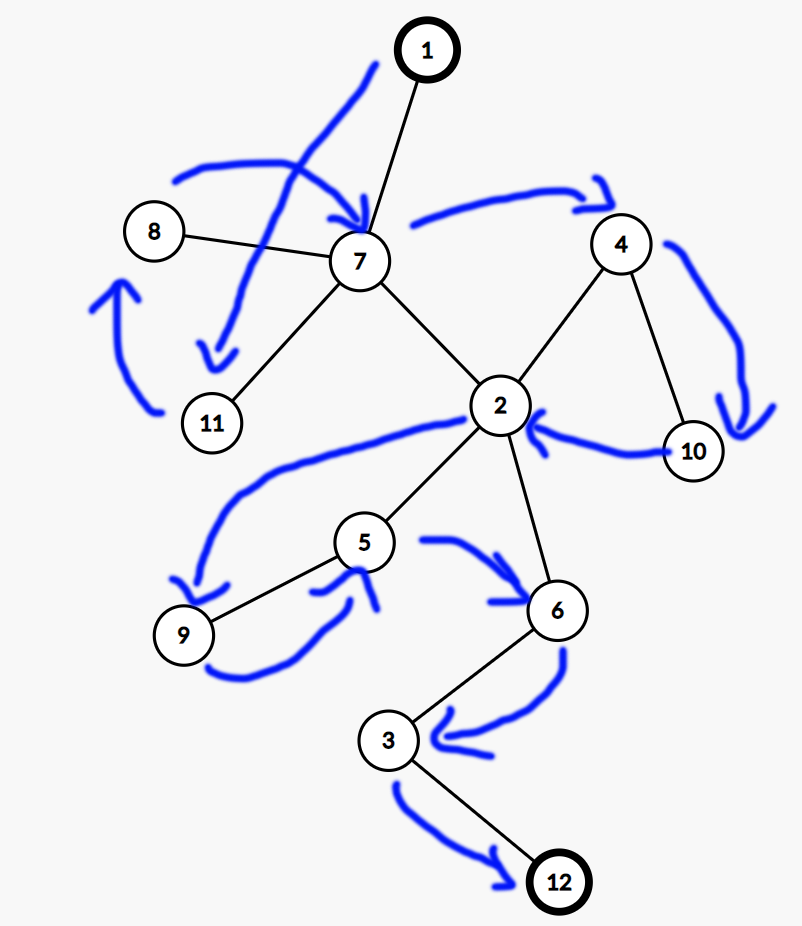
Solution
本题大多数内容均参考自论文《Hamiltonian paths in the square of a tree》。
作者:Jakub Radoszewski and Wojciech Rytter。
原文链接:Hamiltonian paths in the square of a tree
首先我们引入一个定义:caterpillar(毛毛虫),原文定义为 a single path with several leafs connected to it. 简而言之就是其为一棵树,一棵树为 caterpillar 当且仅当去掉其所有叶子节点后剩下的仅为一条单链,如图即为一个 caterpillar。
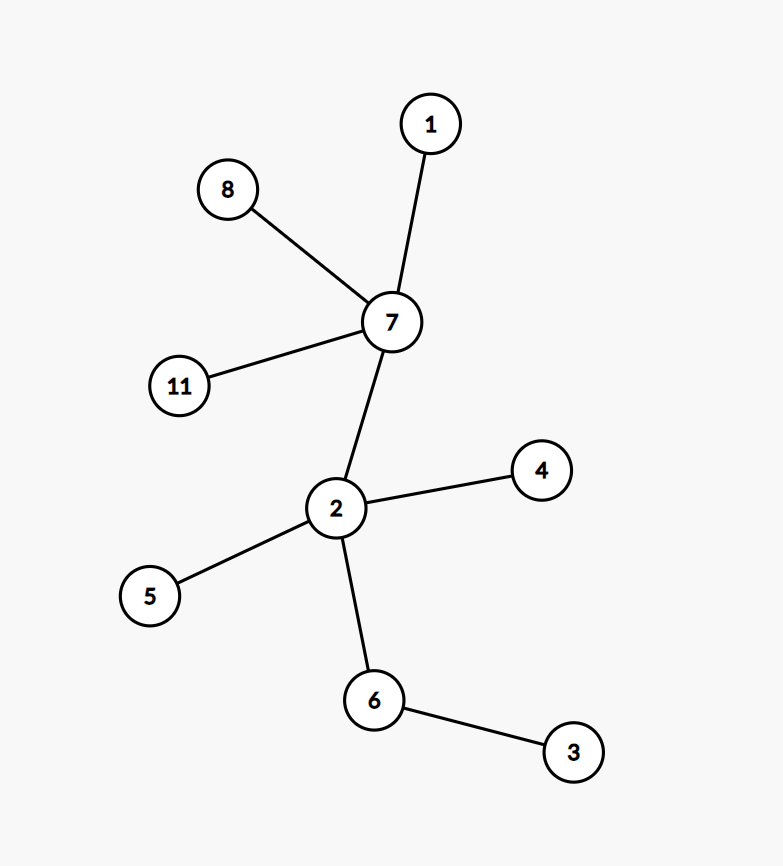
对于其更多的性质及求法,可以去做一下 LG-P3174 [HAOI2009] 毛毛虫,但与本题关联不大,就不再赘述。
现在我们引入下一个定义,对于图 $ G = (V, E) $,我们定义 $ G $ 的 $ k $ 次幂,记作 $ G^k $,为一个基于(或者说完全覆盖,原文为 cover)点集 $ V $ 的图,对于 $ \forall u, v \in V \(,\) u, v $ 之间有边相连当且仅当在 $ G $ 中 $ u, v $ 之间的路径长度不大于 $ k $。我们称 $ G^2 $ 为 the square of $ G $,称 $ G^3 $ 为 the cube of $ G $。
然后我们再引入一个定义:2-connected graph(2-连通图),这个定义类似点双,对于具有割点的图我们定义其为 1-connected graph,则同理 2-connected graph 只得就是至少需要去掉两个顶点才能使图的连通分支增加。
现在我们再引入几个定理:
Lemma 1:对于树 $ T $,图 $ T^2 $ 包含哈密尔顿回路当且仅当 $ T $ 为一个 caterpillar。
Lemma 2:对于树 $ T $,图 $ T^2 $ 包含哈密尔顿路径当且仅当 $ T $ 为一个 horsetail。
证明:咕咕咕。
然后我们继续进行定义。
定义 $ P $ 为 $ G $ 的 k-path 当且仅当 $ P $ 为 $ G^k $ 中的一条路径,同理我们定义 k-cycle。
额外地,我们分别定义 $ G $ 的 kH-path 和 kH-cycle 为 $ G^k $ 中的哈密尔顿路径和哈密尔顿回路。
若 $ G^k $ 包含一个 kH-cycle,我们称 $ G $ 为 k-Hamiltonian(这玩意我也不知道怎么译),同理包含 kH-path 称为 k-traceable。
然后对于 caterpillar,我们额外定义其为 non-trivial 当且仅当其至少含有 $ 1 $ 条边。
我们称 caterpillar 的主链,也就是去掉叶子结点剩下的链,为 spine。
下面开始正文:
我们考虑将原图中 $ 1 $ 到 $ n $ 的路径抽离出来,作为其主干,然后将主干上每个点及其每个子树作为一个新的部分,这里有一个性质,对于这些非主干的部分,有一个性质:若其非 caterpillar,则一定无解,这个东西自己画一下找找性质就会发现很显然,当然严谨的证明我不会。
然后这里我们对于每个主干上的点划分为两类:
- Type A:有不超过 $ 1 $ 个 non-trivial caterpillar。
- Type B:有且仅有 $ 2 $ 个 non-trivial caterpillar。
不难发现,对于 Type A 的节点,若从主干上的节点进入,最后一步一定刚好走到下一个主干节点上,对于 Type B 的节点,在进入时必须直接进入到其任意子树中,否则无解,对于后面的无解判断我们主要也就靠这个性质。
这里有一个性质:若一个点有超过两个的 non-trivial caterpillar 则一定无解,这个依然,自己画一下会发现无论上一步刚好走到这个点还是直接走到某一个子树上,最终都是无解的,路径一定会断在某个子树中,同样严谨的证明我不会。
然后我们额外地定义一个点为 free 当且仅当其为单点,即没有任何子树的主干节点。
如下图例:
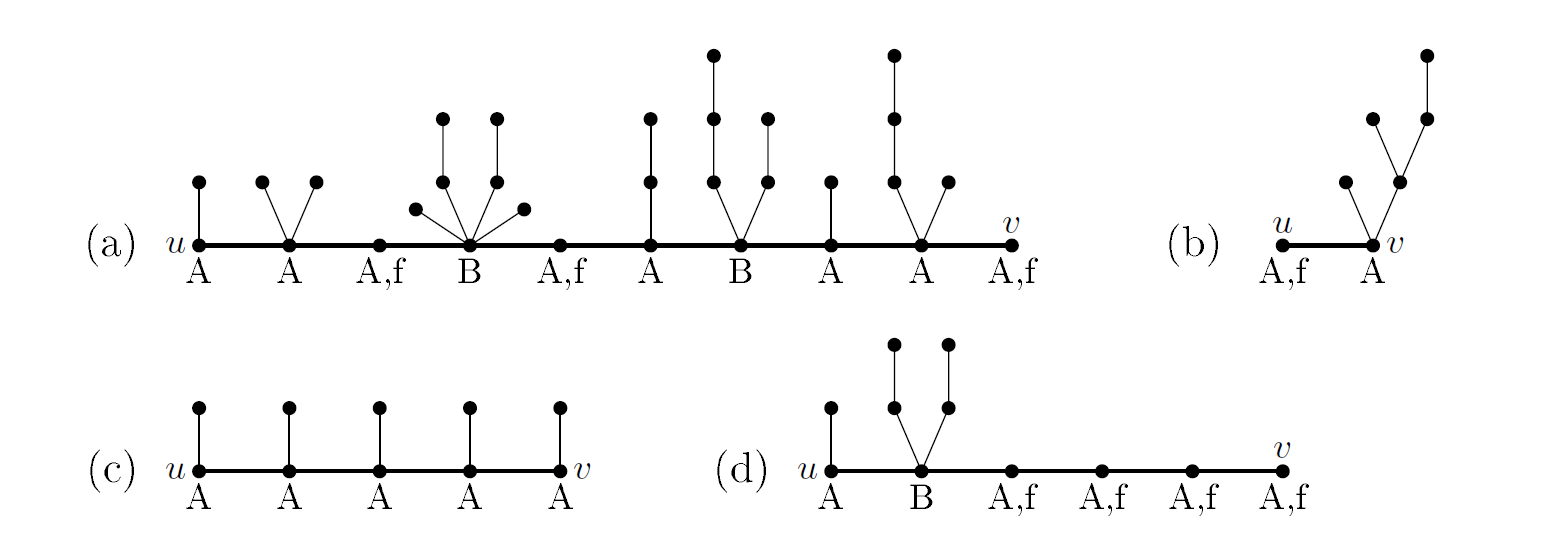
下一个性质:每个 Type B 的节点前后都必须有至少一个 free 节点,否则无解。显然 free 点是可以将进入下一个主干节点和进入下一个主干节点的某一个子节点相互转换的,而 Type A 不能进行这样的转换,两棵 Type B 之间又需要有这样的转换。
对于满足以上所有性质的主干,我们称其为 $ (u, v) $ -horsetail,同时称这整棵树为 horsetail。
现在我们对上面的性质做一个总结:
- 每一个主干节点都为 Type A 或 Type B。
- 在任意两个 Type B 之间都至少有一个 free。
- 在 Type B 之前至少有一个 free。
- 在 Type B 之后至少有一个 free。
- 至少有一个 free。
显然对于上面的四个图例中,(a)(b) 为 horsetail,有解,(c)(d) 非 horsetail,无解。
而对于我们本题的图 $ G $,我们也就需要先判断其是否为 horsetail,如果不是则无解,如果是那么说明 $ G^2 $,也就是按照本题要求构成的图,一定存在一条哈密顿路径,即 Lemma 2。
现在我们对 Lemma 1 进行进一步的阐释:
Lemma 1:任意一个在 caterpillar 上的 2H-cycle 都一定有以下的顺序:我们定义 caterpillar 的 spine 长度为 $ l $,令 spine 为 $ v_1, v_2, \cdots, v_l $,spine 上的叶子为 $ P_1, P_2, \cdots, P_l $,这里我们定义 $ P_i $ 表示一个任意的 $ v_i $ 的叶子的排列。
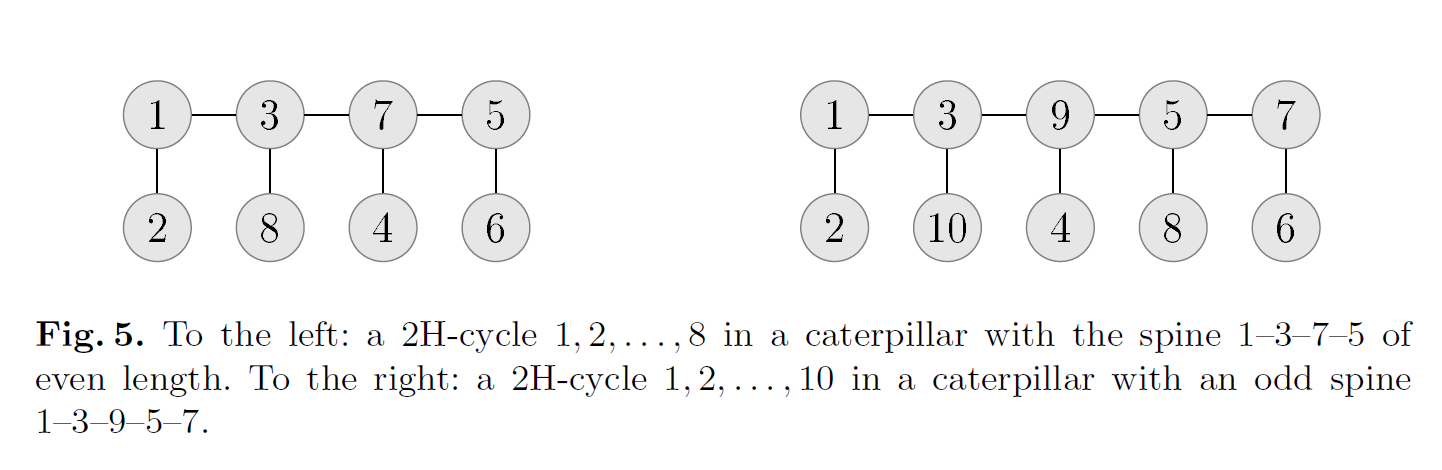
如此图中,显然 $ 1, 2, 3, \cdots, 8, 1 $ 和 $ 1, 2, 3, \cdots, 10, 1 $ 分别为两图的一种 2H-cycle。
所以当我们想要对 horsetail 上的 caterpillar 找到 2H-path 的时候,只需要取 2H-cycle 中的一部分,或者说断开 2H-cycle 中的一条边,如 $ 2, 3, 4, \cdots, 8, 1 $ 这种顺序。
然后再次回到本题,或者说回到 Lemma 2:
对于一个 2H-path $ S $,当树 $ T $ 上的节点被按照分别遍历每个主干节点的每个子树的顺序遍历时,同时我们定义每个主干节点 $ u_i $ 所在子树节点集合为 $ layer(u_i) $,满足每个 $ layer(u_i) $ 都按照特定顺序遍历,我们称树 $ T $ 为 layered,此时我们便可以根据每个主干节点的路径将 $ S $ 分成 $ S_1, S_2, S_3, \cdots $。我们定义一个路径 $ S $ 的起点和终点分别为 $ first(S) $ 和 $ last(S) $,定义主干节点为 main,主干节点直接连接的非主干节点为 secondary,则显然对于每个 $ i \(,\) first(S_i) $ 和 $ last(S_i) $ 均为 main 或 secondary。
对于我们的算法我们首先需要实现一些辅助函数:(为了便于理解,部分函数名与原论文中有微调)
vector < int > BuildCaterpillar(int mp, int S, int T):
对于从 $ S $ 开始 $ T $ 结束的,挂在 horsetail 的主干上的 $ 1 $ 或 $ 2 $ 条 caterpillar 生成 2H-path,这里我们首先需要对这一部分构建一个新的图,将 caterpillar 上所有叶子指向 spine,同时我们需要维护每条 caterpillar 的主干,具体通过代码中的 void BuildSpine(int fa, int p) 实现,我们称 caterpillar 所在的 horsetail 上的主干节点为 $ mp $,那么当 $ mp $ 为 type B 的时候,也就是 non-trivial 的 caterpillar 有两条的时候,我们便可以将前面一条 caterpillar 反过来与其首尾相接,当成同一条 caterpillar,这样最终我们对于形成的 caterpillar 进行如 Lemma 1 地生成 2H-cycle,然后断开其中 $ S \rightarrow T $ 的边(或 $ T \rightarrow S $)即可,同时需要注意如果起始点是在非 non-trivial 的 secondary 节点上,那么我们就需要先遍历其叶子节点,然后最后再遍历其 spine,对于遍历 $ mp $ 的叶子节点,我们通过 void extend(int mp, int unreach1 = -1, int unreach2 = -1) 实现,具体可以看一下代码。
int FindAnySecondaryNode(int p):找到 horsetail 中主干为 $ p $ 的任意一个 secondary 节点。
int FindAnySecondaryNode_PreferablyLeaf(int p):找到 horsetail 中主干为 $ p $ 的任意一个 secondary 节点,且优先找非 non-trivial 的叶子节点。
int FindAnotherSecondaryNode(int p, int lst):找到 horsetail 中主干为 $ p $ 的非 $ lst $ 的另一个 secondary 节点。
然后对于具体的实现,首先我们需要检查一下其是否为无解,也就是前面的检查是否为 horsetail,具体由 void Check(void) 实现。
然后我们算法的核心就是找到 horsetail 的那一条 2H-path,通过 vector < int > Get2HPathHorsetail(void) 实现,大概的思路就是先对第一个节点进行讨论,显然起点一定为 $ 1 $,如果其为 free 节点那么终点也为 $ 1 $,否则一定为其的某一个 secondary 节点,然后构造此 2H-path,对于后面的每个点,如果是 free 节点那么起点终点均为主干点 $ mp $,否则如果上次的终点不是主干节点,这次的起点一定为 $ mp $,终点为优先找非 non-trivial 节点的任意一个 secondary 节点,如果上次的终点是主干节点,那么这次的起点一定为优先找非 non-trivial 节点的 secondary 节点,对于终点,如果该节点是 type B,那么终点也需要为 secondary 节点,找到另外的一个 secondary 节点即可,否则终点为 $ mp $ 即可。
大致的思路就是这样,码量大概 7.5KiB,随后的复杂度是 linear 的,也就是 $ O(n) $ 的。
同时这里提供一个原论文中的对于最后的 Get2HPathHorsetail(void) 的实现,可以选择性地看一下。

Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
/******************************
abbr
mp => mainp
subt => subtree
fa => father
fst => first
lst => last
******************************/
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define EXIT puts("BRAK"), exit(0)
#define MAXN 510000
template<typename T = int>
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[(MAXN << 1) + MAXN];
ROPNEW(ed);
Edge* head[MAXN];
int N;
int mainLen(0);
int fa[MAXN], deg[MAXN];
int mainp[MAXN];
int non_trivial[MAXN];
bool isMainp[MAXN], isFree[MAXN];
void dfs(int p = 1){
for(auto i = head[p]; i; i = i->nxt)
if(SON != fa[p])
fa[SON] = p,
dfs(SON);
}
void InitMainp(void){
int cur = N;
do{
mainp[++mainLen] = cur;
isMainp[cur] = true;
cur = fa[cur];
}while(cur != 1);
mainp[++mainLen] = 1;
isMainp[1] = true;
reverse(mainp + 1, mainp + mainLen + 1);
}
bool isCaterpillar(int fa, int p){
int cnt(0);
for(auto i = head[p]; i; i = i->nxt){
if(SON == fa || deg[SON] == 1)continue;
if(!isCaterpillar(p, SON))return false;
if(cnt++)return false;
}return true;
}
void Check(void){
for(int p = 1; p <= mainLen; ++p){
int mp = mainp[p];
isFree[mp] = true;
for(auto i = head[mp]; i; i = i->nxt){
if(isMainp[SON])continue;
isFree[mp] = false;
if(deg[SON] == 1)continue;
++non_trivial[mp];
if(non_trivial[mp] > 2)EXIT;
if(!isCaterpillar(mp, SON))EXIT;
}
}
int curFree(0);
bool end_with_B(true);
bool exist_free(false);
for(int p = 1; p <= mainLen; ++p){
int mp = mainp[p];
if(isFree[mp]){++curFree; exist_free = true; end_with_B = false; continue;}
if(non_trivial[mp] == 2){
if(!curFree)EXIT;
curFree = 0;
end_with_B = true;
}
}
if(end_with_B || !exist_free)EXIT;
}
int FindAnySecondaryNode(int p){
for(auto i = head[p]; i; i = i->nxt)
if(!isMainp[SON])return SON;
return -1;
}
int FindAnySecondaryNode_PreferablyLeaf(int p){
for(auto i = head[p]; i; i = i->nxt)
if(!isMainp[SON] && deg[SON] == 1)return SON;
return FindAnySecondaryNode(p);
}
int FindAnotherSecondaryNode(int p, int lst){
for(auto i = head[p]; i; i = i->nxt)
if(!isMainp[SON] && SON != lst)return SON;
return -1;
}
namespace Caterpillar{
vector < int > route;
Edge* head[MAXN];
vector < int > spine;
enum type{spineNode = 1, leafNode};
int ffa[MAXN];
void add(int s, int t){
head[s] = new Edge{head[s], t};
ffa[t] = s;
}
void BuildSpine(int fa, int p){
spine.push_back(p);
for(auto i = ::head[p]; i; i = i->nxt){
if(SON == fa)continue;
if(::deg[SON] == 1)add(p, SON);
else BuildSpine(p, SON);
}
}
void extend(int mp, int unreach1 = -1, int unreach2 = -1){
for(auto i = head[mp]; i; i = i->nxt){
if(SON == unreach1 || SON == unreach2)continue;
route.push_back(SON);
}
}
vector < int > BuildCaterpillar(int mp, int S, int T){
route.clear();
spine.clear();
route.push_back(S);
if(S == T)return route;
spine.push_back(mp);
bool exist_caterpillar(false);
for(auto i = ::head[mp]; i; i = i->nxt){
if(isMainp[SON])continue;
if(deg[SON] == 1)add(mp, SON);
else{
if(!exist_caterpillar)exist_caterpillar = true;
else reverse(spine.begin(), spine.end());
BuildSpine(mp, SON);
}
}
vector < pair < int, type >/*spine_node_pos, spine or leaf*/ > temp;
vector < pair < int, type >/*spine_node_pos, spine or leaf*/ > unextended;
for(int i = 0; i < (int)spine.size(); ++i)
temp.push_back({spine.at(i), !(i & 1) ? spineNode : leafNode});
for(int i = (int)spine.size() - 1; i >= 0; --i)
temp.push_back({spine.at(i), (i & 1) ? spineNode : leafNode});
for(auto it = temp.begin(); it < temp.end(); ++it)
if(it->second == spineNode || head[it->first])unextended.push_back(*it);
#define LEFT(x) (x == 0 ? (int)unextended.size() - 1 : x - 1)
#define RIGHT(x) (x == (int)unextended.size() - 1 ? 0 : x + 1)
auto Beg = deg[S] == 1 ? make_pair(ffa[S], leafNode) : make_pair(S, spineNode);
auto End = deg[T] == 1 ? make_pair(ffa[T], leafNode) : make_pair(T, spineNode);
int begPos = -1; while(unextended.at(++begPos) != Beg);
if(Beg.second == leafNode)extend(Beg.first, S, T);
if(unextended.at(LEFT(begPos)) == End)
for(int j = RIGHT(begPos); unextended.at(j) != End; j = RIGHT(j))
unextended.at(j).second == spineNode
? route.push_back(unextended.at(j).first)
: extend(unextended.at(j).first);
else
for(int j = LEFT(begPos); unextended.at(j) != End; j = LEFT(j))
unextended.at(j).second == spineNode
? route.push_back(unextended.at(j).first)
: extend(unextended.at(j).first);
if(End.second == leafNode && Beg != End)extend(End.first, S, T);
route.push_back(T);
return route;
}
}
vector < int > Get2HPathHorsetail(void){
vector < int > ret;
int fst = mainp[1];
int lst = isFree[mainp[1]]
? mainp[1]
: FindAnySecondaryNode(mainp[1]);
auto tmp = Caterpillar::BuildCaterpillar(mainp[1], fst, lst);
ret.insert(ret.end(), tmp.begin(), tmp.end());
for(int i = 2; i <= mainLen; ++i){
int w = mainp[i];
if(isFree[w])fst = lst = w;
else if(!isMainp[lst])
fst = w,
lst = FindAnySecondaryNode_PreferablyLeaf(w);
else
fst = FindAnySecondaryNode_PreferablyLeaf(w),
lst = non_trivial[w] == 2
? FindAnotherSecondaryNode(w, fst)
: w;
auto cp = Caterpillar::BuildCaterpillar(w, fst, lst);
ret.insert(ret.end(), cp.begin(), cp.end());
}
return ret;
}
int main(){
N = read();
for(int i = 1; i <= N - 1; ++i){
int s = read(), t = read();
head[s] = new Edge{head[s], t};
head[t] = new Edge{head[t], s};
++deg[s], ++deg[t];
}
dfs();
InitMainp();
Check();
auto ans = Get2HPathHorsetail();
for(auto i : ans)printf("%d\n", i);
return 0;
}
template<typename T>
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
写在后面
就是这道不怎么友好的题,我做的时候网上几乎没有题解,只能找到几篇说的很简略的题解,然后没办法只能去自己翻英文论文,然后一个一个查词,在我快要写完这道题的时候,才突然发现 Luogu 上多出来了两篇题解。。
然后就是调这道题,一共交了 $ 70+ $ 次才过了这道题,自己写完之后怎么改都是 $ 70 $ pts,Luogu 上下不了数据,hydro 等没有 SPJ,没办法只能开始把每一部分的代码对着大佬的代码改,最后几乎把整篇代码都重构了一遍才找到错误,只是调代码就调了一天半,不过至少最后还是过了。
UPD
update-2022_09_26 完成 Bytecomputer Taxis Colorful Chain
update-2022_09_27 完成 Walk Tales-of-seafaring
update-2022_09_28 完成 Polarization Take-out
update-2022_09_29 完成 Inspector Tower Defense Game
update-2022_10_03 完成 Triumphal arch Price List
update-2022_10_04 完成 Laser
update-2022_10_04 跳过 Tapestries Maze
update-2022_10_08 修改了很多小错误
update-2022_10_09 完成 Multidrink
update-2022_10_10 修复 Multidrink 的错误


 浙公网安备 33010602011771号
浙公网安备 33010602011771号