题解 CF9B 【Running Student】

题解 CF9B 【Running Student】

Description

一位可怜的学生再次遭遇不幸——他要考试迟到了。

【他所在的地区可以看成一个平面直角坐标系，】他跑到了位于(0,0)处的公交车站，上了一辆小巴。这辆小巴沿x轴向x轴正方向行驶。

这个学生知道这样一些事：

这辆小巴将停靠n个站点，其中第i个站点位于(xi,0)处。

每一个站点的坐标都不相同。

这辆小巴将以速度vb匀速行驶。

小巴停站的时间很短，可以忽略不计。

乘客只能在站点上下车。

乘客最晚必须在终点站下车。

考试地点在(xu,yu)处。

他可以用vs的速度匀速从一个车站跑向考试地点。

在平面直角坐标系内，两点间的距离可以用\(\sqrt((x_1 - x_2)^2 + (y_1-y_2)^2)\)表示

他不能在上车站下车。 这个可怜的学生想用尽可能短的时间到达考试地点。请你帮他选择一个可以达到他的目的的下车地点。如果有多个满足的下车地点，请输出离考试地点最近的一个。

输入输出格式

输入格式

输入的第一行包括三个整数：n,vb和vs。第二行包括n个升序排序的非负整数，第i个数表示第i个站点的横坐标。第1个数一定等于0。第三行包括两个整数，依次为考试地点的横坐标xu和纵坐标yu。

输出格式

输出一行，一个整数，他应该下车站的序号。

说明

数据范围

保证2<=n<=100,1<=vb,vs<=1000,0<=xi<=10^{5,0<=|xu|,|yu|<=10}5

Solution

对于每一个点，我们枚举是否下车，计算各种距离取最小值即可，时间复杂度 \(\mathcal{O(n)}\)。
画一个图：

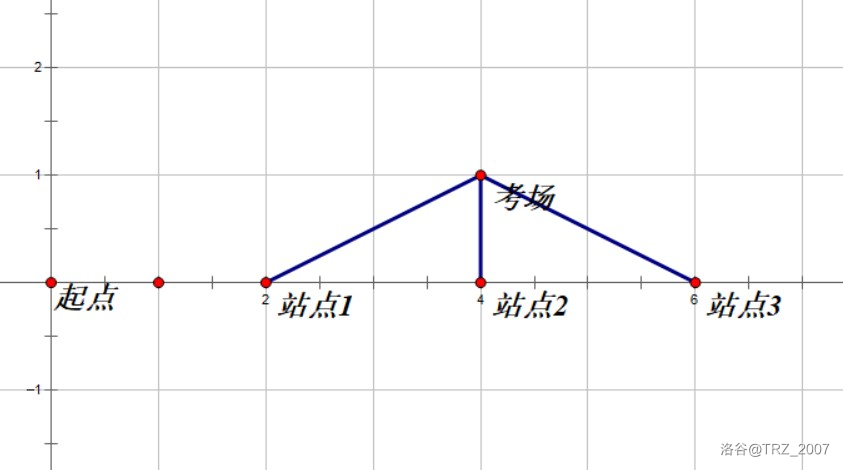
通过图可以看出，应该在二号站点下车。

几个坑点

• 1:他不能在起点下车，所以枚举时应该从2（即图中站点1）开始枚举。
• 2：如果有多个满足的下车地点，请输出离考试地点最近的一个。所以我们需要存下离站点最近的点进行比对。

Code

#include <bits/stdc++.h>
using namespace std;

const int N = 109;

double dis[N],x[N],u,v,ans,ansd;
int n,v1,v2,cnt;

int main() {
	scanf("%d %d %d",&n,&v1,&v2);
	for(int i = 1;i <= n;i++) {
		scanf("%lf",x + i);
	}
	scanf("%lf %lf",&u,&v);
	for(int i = 1;i <= n;i++) {
		dis[i] = sqrt((u - x[i]) * (u - x[i]) + v * v);
	}
	ans = 1e9 + 10; ansd = 1e9 + 10;
	for(int i = 2;i <= n;i++) {
		if(ans >= dis[i] / v2 + x[i] / v1 && ansd > dis[i]) {
			ans = dis[i] / v2 + x[i] / v1;
			ansd = dis[i];
			cnt = i;
		}
	}
	printf("%d\n",cnt);
	return 0;
}