【做题记录】BJOI2016 水晶

• \(\text{BJOI2016}\) 水晶

  • 算法：网络流

题目：

一个六边形网格的坐标用 \((x,y,z)\) 来描述一个单元的位置，表示从原点开始按如图所示的 \(x,y,z\) 方向各走若干步之后到达的地方。

已知有 \(n\) 个水晶，并给出坐标与价值。

定义能量源为满足坐标 \((x+y+z)\equiv0 \pmod3\)，若其上面有水晶，则价值加上 \(10\%\)。

炸掉一些水晶，使得：

1. 没有 \(a\) 共振：如果三块水晶所在的单元两两相邻地排成一个三角形，那么会引起 \(a\) 共振。

2. 没有 \(b\) 共振：如果三块水晶所在的单元依次相邻地排成一条长度为 \(2\) 的直线段，且正中间的单元恰好有能量源，那么会引起 \(b\) 共振。

求剩下水晶最大价值。

\(n\le 5\times 10^4\)。

---

题解：

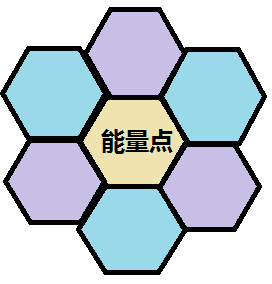
考虑对于一个能量源 \((x,y,z)\)，将它的周围六个点分成两类：

黑色：\((x-1,y,z),(x,y-1,z),(x,y,z-1)\)

白色：\((x,y,z+1),(x,y+1,z),(x+1,y,z)\)

那么，有一个重要性质：

若选择了能量点，则黑色白色不能同时出现。

考虑证明。（图中的紫色是白、蓝色是黑，红色表示选择的水晶）

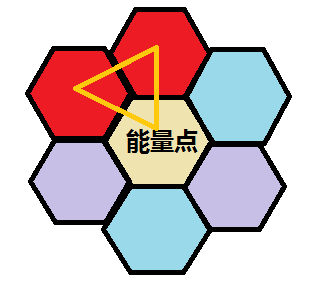
1. 黑白相邻

如图，形成了 \(a\) 共振。

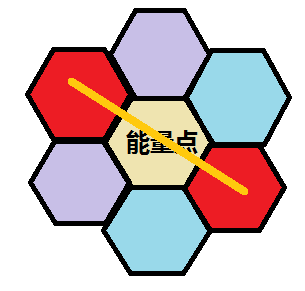
2. 黑白不相邻

形成了\(b\) 共振。

所以考虑把 \(\bmod 3\) 意义下的三种点分别拆点。

将一个点拆成两个，中间一条边表示选或者不选，三类顺次连长度为INF的边，跑最小割即可。

然后源点连 \(1\) 的点，\(1\) 连 \(0\)，\(0\) 连 \(2\)，\(2\) 连 汇点，答案为水晶的总能量减最大流。

这样就保证了黑白不相邻。

和王者之剑非常像。